Обработка результатов моделирования

Для получения оценок математического ожидания (среднего значения) и дисперсии последовательности значений СВ, полученных в GPSS необходимо использовать блоки сбора статистики TABLE и TABULATE.

Оператор описания таблицы TABLE имеет следующий формат:

<NAME> TABLE <A>,<B>,<C>,<D>

Оператор определяет аргумент, а также число и ширину частотных интервалов.

Метка NAME определяет имя таблицы.

В поле А задается аргумент таблицы - элемент данных, чье частотное распределение будет табулироваться. Операнд может быть именем, целым, СЧА или СЧА*<параметр>.

В поле В задается верхний предел первого интервала. Операнд может целым или именем.

В поле С задается ширина частотного интервала - разница между верхней и нижней границей каждого частотного класса. Операнд может быть положительным целым.

В поле D задается число частотных интервалов. Это число не может превышать 8191. Операнд может быть положительным целым.

Для сбора элементов данных сообщение должно войти в блок TABULATE с тем же именем таблицы, что определено в блоке TABLE.

Когда сообщение входит в блок TABULATE, оценивается аргумент таблицы (операнд А в операторе TABLE). Если он меньше или равен операнду В в операторе TABLE, то выбирается первый частотный класс таблицы. Если аргумент таблицы не подходит для этого класса, то класс выбирается путем деления значения аргумента на операнд С оператора TABLE. Нижняя граница частотного класса включается в предыдущий класс. Если таблицы не достаточно для размещения этого значения, то выбирается последний частотный интервал. Затем выбирается целое из частотного класса и счетчик увеличивается на величину, определяемую операндом В оператора TABULATE. По умолчанию увеличение происходит на 1. В конце работы оператора TABULATE изменяются значения среднего и стандартного отклонения аргумента таблицы.

Таблица может быть переопределена или переинициализирована другим оператором TABLE, с той же самой меткой, что и первая.

Стандартные числовые атрибуты, связанные с описываемым опера-

тором, следующие:

- ТВ - среднее значение аргумента;

- ТС - число входов в таблицу;

- ТD - стандартное отклонение.

Блок, связанный с оператором TABLE - TABULATE.

Блок TABULATE имеет следующий формат:

TABULATE <А>,[<B>]

Блок TABULATE табулирует текущее значение заданного аргумента. Способ табуляции зависит от режима работы таблицы, который определяется оператором описания таблицы TABLE.

В поле А задается номер или имя таблицы, в которую табулируется значение аргумента. Таблица должна быть определена оператором описания TABLE.

В поле В задается число единиц, которые должны быть занесены в тот частотный интервал, куда попало значение аргумента. Если поле В пусто, эта величина полагается равной единице.

Когда сообщение входит в блок TABULATE, то для нахождения таблицы используется операнд А. Если такой таблицы нет, то возникает ошибка выполнения. Таблица должна быть определена оператором TABLE. Таблица изменяется в соответствии с операндами оператора TABLE.

Пример использования блоков TABLE и TABULATE.

TT TABLE M1,40,50,8

EXP1 FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

GENERATE 100,FN$EXP1

ADVANCE 100,FN$EXP1

TABULATE TT

TERMINATE 1

START 100

Здесь М1 – константа (стандартный числовой атрибут), которая связана с каждым транзактом и хранит время пребывания транзакта в модели. Время пребывания транзакта в модели определяется блоком ADVANCEи распределено по показательному закону с 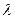=1/100. Строится частотное распределение, вычисляются оценки математического ожидания и среднеквадратического отклонения для М1, т.е.для времени пребывания транзакта в модели. Граница первого интервала задана 40; ширина интервала группирования – 50; число интервалов группирования – 8. Все эти параметры задаются опытным путем.

Ниже приведен фрагмент отчета, выдаваемый GPSS по результатам работы программы.

TABLE MEAN STD.DEV. RANGE RETRY FREQUENCY CUM.%

TT 101.032 101.889 0

_ - 40.000 38 38.00

40.000 - 90.000 23 61.00

90.000 - 140.000 9 70.00

140.000 - 190.000 8 78.00

190.000 - 240.000 10 88.00

240.000 - 290.000 6 94.00

290.000 - 340.000 5 99.00

340.000 - _ 1 100.00

Mean – это среднее значение или оценка математического ожидания;

STD.DEV – это оценка среднеквадратического отклонения;

Range – интервалы группирования;

FREQUENCY – количество наблюдений, попавших в каждый интервал.

Таким образом, погрешность в оценке математического ожидания составила:

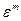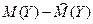= =100-101.032=-1.032

Погрешность в оценке среднеквадратического отклонения составила:

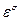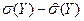= =100-101.889=-1.889.

Таким образом, точность имитационного моделирования значений СВ по методу кусочной аппроксимации функции плотности распределения вероятностей в среде GPSS достаточно высокая.

Для построения гистограммы необходимо выбрать после выполнения программы пункт меню Window/Simulation Window/Table Window. Далее в открывшемся диалоговом окне задать имя таблицы (в данном примере TT). Вид гистограммы приведен на рис. 1.

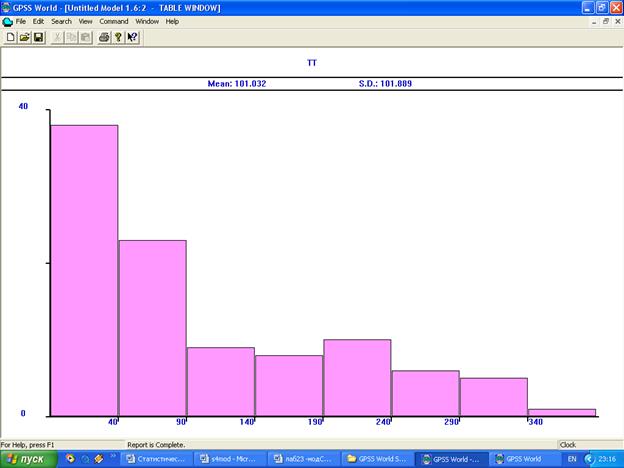Рис. 15.Гистограмма значений СВ Y

Визуальный анализ гистограммы позволяет сделать вывод о согласии выборочных значений СВ Y с моделью экспоненциального распределения.

11.5. Основные направления развития инструментальных средств моделирования

Языки имитационного моделирования позволяют за сравнительно короткий срок составлять программные модели довольно сложных систем. К сожалению, такие модели обладают низкой способностью отвечать на вопросы типа "а что, если ...", поскольку это именно те вопросы, которые наиболее полезны, так как они способствуют более глубокому пониманию проблемы и поиску лучших способов оценки возможных действий. Для ответа на подобные вопросы часто приходится непосредственно изменять программный код модели, что повышает затраты времени на анализ системы. При использовании языков имитационного моделирования возникает также другая проблема: затраты на изучение и освоение языка, тем более, что эти языки оперируют абстрактными понятиями, в то время как экспериментатор часто является специалистом в той области, которой принадлежит моделируемая система, и применяет специфическую терминологию, что может значительно осложнить освоение языка исследователем.

В настоящее время языки имитационного моделирования получили дальнейшее развитие в виде визуальных средств моделирования, где исследователь оперирует не командами и операторами языка, а объектами, представляемыми в графическом виде. Примером такой системы может служить ARENA. Визуальные средства моделирования частично снимают проблемы языков имитационного моделирования, описанные чуть выше, но в то же время основные из них остаются, например, освоение исследователем абстрактных терминов, используемых в этих средствах.

Вторым направлением развития инструментальных средств имитационного моделирования являются узкоспециализированные моделирующие программные комплексы. Преимуществами таких комплексов является быстрая реализация модели, использование терминологии, понятной исследователю, применяющему это средство, позволяют быстро отвечать на вопросы типа "а что, если ...".

Список литературы

1. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Основы моделирования и первичная обработка данных. – М.: «Финансы и статистика», 1983. – 471 с.

2. Бусленко Н.П. Моделирование сложных систем. – М.: Наука, 1978. – 399 с.

3. Вентцель Е.С. Исследование операций. – М.: Высшая школа, 2000. – 550 с.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2004. – 404 с.

5. Губарев В.В. Вероятностные модели / Новосиб. электротехн. ин-т. – Новосибирск, 1992. – Ч.1. – 198 с; Ч.2. – 188 с.

6. Губарев В.В. Системный анализ в экспериментальных исследованиях. – Новосибирск: Изд-во НГТУ, 2000. – 99 с.

7. Денисов А.А., Колесников Д.Н. Теория больших систем управления: Учеб. пособие для вузов. – Л. Энергоиздат, 1982. – 288 с.

8. Моделирование систем. Практикум: Учеб. пособие для вузов/Б.Я. Советов, С.А. Яковлев. – 2-е изд., перераб. и доп. – М.: Высшая школа, 2003. – 295 с.

9. Система программного обеспечения для имитационного моделирования на GPSS/PC. Версия 2. – Калинин: Центрпрограммсистем, 1989. – 200 с.

10. Советов Б.Я., Яковлев С.А. Моделирование систем (3-е изд.). – М.: Высшая школа, 2001. – 420 с.

11. Теория случайных процессов и ее инженерные приложения: Учеб. пособие для вузов/Е.С. Вентцель, Л.А. Овчаров. – 3-е изд. перераб. и доп. – М.: Издательский центр «Академия», 2003. – 432 с.

12. Томашевский В., Жданова Е. Имитационное моделирование в среде GPSS. – М.: Бестселлер, 2003. – 416 с.

13. Хачатурова С.М. Математические методы системного анализа: Учеб. пособие. – Новосибирск: Изд-во НГТУ, 2004. – 124 с.

14. Шрайбер Т.Дж. Моделирование на GPSS. – М.: Машиностроение, 1980. – 593 с.

15. http://www.gpss.ru. Сайт, посвященный системе моделирования GPSS.