Результаты дисперсионного анализа

Варьирование	Сумма квадратов	Степень свободы (ν)	Средний квадрат (дисперсия –S2)	Значение критерия F
фактическое	теоретическое
Fфакт	F05
Общее Су
Повторений Ср
Вариантов Сv
Случайное (остаточное) Сz

6) Число степеней свободы (ν) рассчитывается:

для общей дисперсии (варьирования): ν = nl - 1=

для дисперсии повторений: ν _p = n - 1=

для дисперсии вариантов: ν _v = l- 1=

для остаточной дисперсии ν _z = (n - 1)( l –1 )=

7) Проведите расчет дисперсий и критерия F_факт

Дисперсия вариантов S²_v= ___________________________________________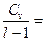

Дисперсия ошибок S²_z= _________________________________________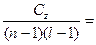

Критерий F_факт= ________________________________________________________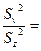

В приложении 2 найдите F₀₅(табл)=

при числе степеней свободы ν _v= и ν _z =

Сравнив F_факт с F₀₅, установите наличие нулевой гипотезы в опыте, или укажите, что она отвергается

________

8) Рассчитайте ошибку опыта в абсолютных величинах и ошибку разности:

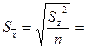
S_d = _________________________________________________________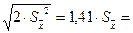

9)Рассчитайте наименьшую существенную разницу (НСР₀₅) и оцените по ней существенность разницы урожаев между вариантами.

НСР₀₅= t₀₅ · S_d= ______________________________________________________________

____

при v_zост=__________________ t₀₅=_____________________________

Сделайте выводы и дайте рекомендации производству._________________

________________________________________________

Дисперсионный анализ данных урожайности с применением корректирующего фактора (поправки) и произвольного начала А (модель 2-я).

Контрольные вопросы

В каком случае следует использовать произвольное начало А?	Какое число принимается за произвольное начало А?
Какую роль преследует введение корректирующего фактора – С? Укажите формулу для его расчёта.	В чём различие в проведении расчётов при использовании условной средней А, близкой к средней арифметической опыта и А, равной нулю?

Последовательность выполнения задания

1) Подготовьте таблицу урожая (табл. 9), используя данные табл. 2.

Таблица 9

Урожайность_______________________________________________________________

________________

Вариант	Урожайность, ц/га (х)	Сумма по вариантам (V)	Средняя по вариантам ( )
I	II	III	IV
1.
2.
3.
4.
Сумма по повторениям (Р)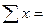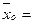

2) Составьте таблицу отклонений от произвольного начала А и квадратов отклонений.

Таблица 10

Таблица отклонений от произвольного начала А и квадратов отклонений

Вариант	Отклонения от произвольного начала (х - А)	Сумма отклонений (VА)	Квадраты отклонений (х - А)2	(VА)2
I	II	III	IV	I	II	III	IV
1.
2.
3.
4.
Сумма от- клоненний РА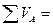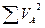

Проверка правильности расчетов проводится по равенству: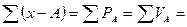

3) Рассчитайте корректирующий фактор.

Общее число наблюдений N=ln=

Корректирующий фактор С=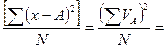

____

4) Рассчитайте виды варьирования (суммы квадратов):

общее С_у= 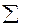(х - А)² – С= ____

____

____

повторений ____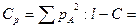

____

____

вариантов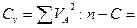

____________

остаточное (ошибка) C_z= C_y – (C_p+C_v)=___________________________________

____

____

5) Составьте сводную таблицу дисперсионного анализа (табл.11).

Таблица 11