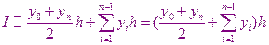Метод возмущения параметров.

Тема №5

Решение систем не линейных уравнений.

Метод 18

Простой Итерации

Пусть требуется найти решение системы из n уравнений с t неизвестными.

…………………..

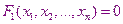
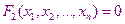
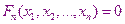
В общем случае прямых методов решения систем не линейных уравнений нет. Единственным методом решения является итерационный.

Самый простой метод решения – это метод простой итерации. Преобразуем исходную систему к такому виду:

…………………..

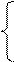
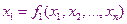
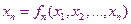
Это преобразование можно произвести всегда, причем различным образом.Затем следует задать начальное приближение: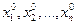

И тогда из 1-го уравнения мы получим:

…………………..

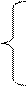
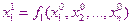
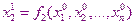
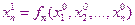
При использовании метода простой итерации успех во многом зависит от удачного выбора начального приближения (чем дальше начальное приближение от истинного значения, тем больше вероятность расхождения итерационного процесса).

Для системы существует область сходимости, если начальное приближение попадает в эту область, то итерационный процесс будет сходиться, не попадает – расходиться.

Чем больше число неизвестных, тем меньше область сходимости, тем труднее получить решение на промежутке т.к. обеспечить сходимость метода простой итерации не всегда удаётся.

Метод 19

Метод Ньютона для систем уравнений.

Обладает гораздо более быстрой сходимостью и большей областью сходимости.

В основе метода Ньютона лежит представление всех уравнений системы в виде ряда Тейлора с отброшенными членами содержащие 2-ые и более высоких порядков производные.

…………………..

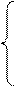
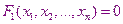
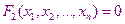
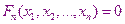
Представим решение на k+1 итерационном шаге в виде

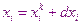
Нашей целью является нахождение небольших поправок к решению.

Для этого подставим эти решения в уравнения системы и разложим в ряд Тейлора

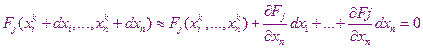
В результате получиться система уравнений вида:

……………………………………..

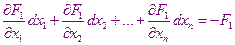
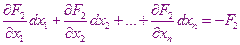
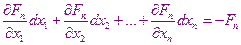
В этой системе все правые части вычисляются при уже найденных , ,…, .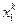

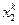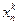В результате мы получили систему линейных уравнений (СЛУ) относительно неизвестных величин. После того как решение системы найдено (решаем методом Гаусса), получаем решение на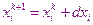

Метод 20

Метод возмущения параметров.

Нам дана система

…………………..

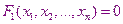
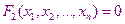
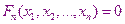
Наряду с системой, решение которой необходимо найти, мы решаем систему из такого же числа уравнений решение которой известно.

……………………

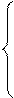
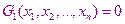
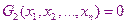
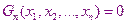
Деформируя (возмущая) уравнение системы с известным решением, с помощью конечного числа N (малых приращений), преобразуем их к системе, решение которой надо найти.

Деформацию можно проводить различными способами.

Например, на шаге деформации с номером k деформацию можно записать в виде

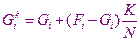, где i – это номер уровня.

Если число шагов деформации N достаточно велико, то деформация системы на каждом шаге будет не значительна.

Решение системы (G) можно использовать как начальное приближение неизвестных для итерационного решения полученного при первой деформации системы. Так как эта система при достаточно больших значениях N мало отличается от предыдущей то, вероятно, что сходимость для деформируемой системы будет обеспечена.

После этого производится вторая деформация. И используя решения, полученные для первой деформации в качестве начального приближения, найдём корень системы после второй деформации. В конце счета, когда номер деформации k= N решаемая система становится эквивалентной исходной (F).

Применение может привести к значительному увеличению объёма вычислений. Однако при этом возрастают шансы на то, что метод сойдётся.

Тема №6

Численное интегрирование.

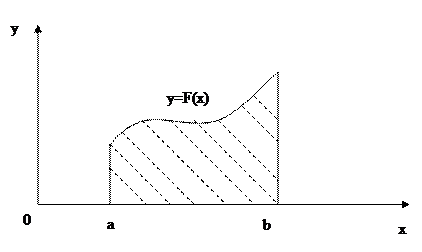
Определённый интеграл

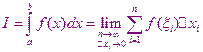где,

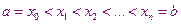
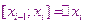
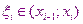
Часто возникает задача численного интегрирования, например в таких случаях когда:

1)аналитически, через элементарные функции интеграл не берётся;

2)численное интегрирование необходимо использовать, если подинтегральная функция задана в табличном виде.

При численном интегрировании используется определение интеграла и его геометрического смысла. Приближенное значение интеграла мы получим, если в интегральной сумме ограничимся конечным числом слагаемых.

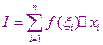
Метод 21

Метод прямоугольников.

Простейшим методом численного интегрирования является метод прямоугольников. В этом методе интеграл вычисляется с помощью усеченной интегральной суммы, а в качестве точки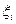

берётся середина отрезка 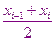. При вычислении можно использовать правую или левую сторону этого отрезка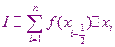

Метод 22

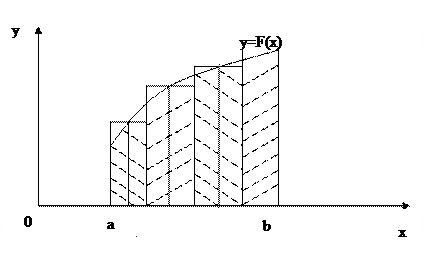
Метод трапеции

В этом методе интеграл, приближенно заменяется на сумму площадей трапеций, образующихся после замены графика функции 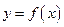ломаной, соединяющей точки .

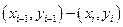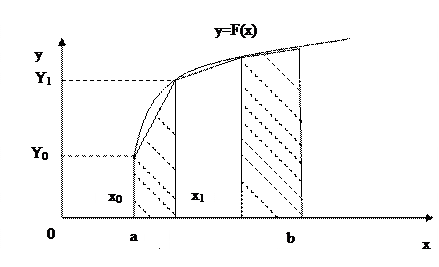
Площадь трапеции с номером 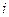равняется

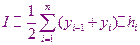
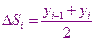
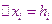-шаг интегрирования

Для практического использования важен случай интегрирования с постоянным шагом 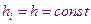тогда