Тема 7 Производная и дифференциал

Лекция 2.7.1 «Функция. Предел. Непрерывность»

Учебные вопросы:

1. Функция

2. Предел. Непрерывность

Функция

Постоянная величина – это величина, сохраняющая одно и то же значение. Если величина сохраняет постоянное значение лишь в условиях данного процесса, то она называется параметром.

Переменная – это величина, которая может принимать различные числовые значения.

Если каждому элементу ставится в соответствие вполне определенный элемент , то говорят, что на множестве Х задана функция .

При этом х называется независимой переменной или аргументом, y – зависимой переменной, а буква обозначает закон соответствия.

Множество Х называется областью определения(существования) функции, а множество Y – областью значений функции.

Способы заданий функций:

1. Аналитический способ. В этом случае функция задается формулой вида .

2. Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции .

3. Графический способ состоит в изображении графика функции – множества точек плоскости , абсциссы которых есть значения аргументов х, а ординаты – соответствующие им значения функции .

4. Словесный способ, если функция описывается правилом ее составления.

Основные свойства функций:

1. Четность и нечетность. Функция называется четной, если для любых значений х из области определения , и нечетной, если . В противном случае функция 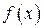называется функцией общего вида.

Пример. Функция – четная, – нечетная, – общего вида.

График четной функции симметричен относительно оси ординат, а нечетной функции – относительно начала координат.

2.

Монотонность. Функция 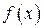называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции (см. рисунок). Если для любых , , – функция 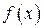возрастающая, – функция 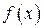убывающая. Возрастающие и убывающие функции называются монотонными.

3. Ограниченность. Функция называется ограниченной на промежутке Х, если существует такое число , что для любого выполняется неравенство .

4. Периодичность. Функция называется периодической с периодом , если для любого .

Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной: , .

Функция называется неявной, если она задана уравнением 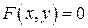, не разрешенным относительно зависимой переменной: .

Пусть есть функция от независимой переменной х, определенной на промежутке Х с областью значений Y. Поставим в соответствие каждому единственное значение , при котором . Тогда полученная функция , определенная на промежутке Y с областью значений Х, называется обратной для функции 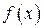. Обратную функцию обычно обозначают (это не степень!). Примеры: для функции обратной будет , для функции обратной будет

Можно доказать, что для любой строго монотонной функции существует обратная функция. Если построить графики взаимно обратных функций в одних обозначениях ( 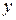выраженном через 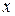), то они будут симметричны относительно биссектрисы 1-го и 3-го координатных углов (прямой, проходящей под углом из начала координат) (см. рис.)..

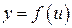Пусть функция есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u, в свою очередь, является функцией 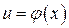от переменной х, определенной на множестве Х с областью значений U. Тогда называется сложной функцией (композицией функций, функцией от функции).

Например, – сложная функция, т.к. ее можно представить в виде , где .

Основные элементарные функции:

1. Степенная функция: (и ее частные виды , ).

2. Показательная функция: .

3. Логарифмическая функция: .

4. Тригонометрические функции: , , , .

5. Обратные тригонометрические функции: , , , .

Пусть задан график функции . Тогда справедливы следующие утверждения:

1. График функции есть график , сдвинутый на единиц вдоль оси Oх; при – влево, при – вправо.

2. График функции есть график , сдвинутый единиц вдоль оси Oy; при – вверх, при – вниз.

3. График функции есть график :

- растянутый в m раз вдоль оси Oy, при ;

- сжатый в m раз вдоль оси Oy, при ;

- растянутый в m раз вдоль оси Oy и отраженный зеркально относительно оси Ox, при ;

- сжатый в m раз вдоль оси Oy и отраженный зеркально относительно оси Ox, при .

4. График функции есть график :

- сжатый в k раз вдоль оси Ox, при ;

- растянутый в k раз вдоль оси Ox, при ;

- сжатый в k раз вдоль оси Ox и отраженный зеркально относительно оси Oy, при ;

- растянутый в k раз вдоль оси Ox и отраженный зеркально относительно оси Oy, при .

Предел. Непрерывность

Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число ,то говорят, что задана числовая последовательность : . Другими словами, числовая последовательность – это функция натурального аргумента .

Числа называются членами последовательности, а число – общим или n-м членом данной последовательности.

Примеры: 2, 4, 6, …, 2n, … (монотонная неограниченная последовательность четных чисел); 1, 0, 1, 0, … (немонотонная ограниченная последовательность чередующихся чисел 0 и 1).

Число А называется пределом числовой последовательности , если для любого сколь угодно малого найдется такой номер , зависящий от , что для всех членов данной последовательности с номерами верно неравенство

(7.1)

Предел числовой последовательности обозначается или при . Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Смысл определения: для достаточно больших n члены последовательности сколь угодно мало отличаются от числа А, по абсолютной величине меньше, чем на e, каким бы малым оно ни было.

Число А называется пределом функции y = f(x) при х, стремящемся к бесконечности, если для любого e > 0 найдется такое S > 0, что для всех |х| > S верно неравенство

| f(x) – A | < e (7.2)

Предел функции обозначается f(x) = A, или f(x) ® A при х ® ¥.

Это предел функции в бесконечности.

Число А называется пределом функции f(x) при х ® х₀, если для любого e > 0 найдется такое d = d(e) > 0, что для всех x ¹ x_0, |х – x₀| < d выполняется неравенство | f(x) – A | < e.

Смысл определения: для всех значений х, достаточно близких к х₀, значения f(x) как угодно мало отличаются от числа А.

Замечание 1. Определение предела не требует существования функции в самой точке х₀, поскольку предполагается, что х стремится к х₀, но не достигает значения х₀. Поэтому наличие или отсутствие предела при х ® х₀ определяется поведением функции в окрестности точки х₀, но не связано с существованием функции в самой точке х₀.

Замечание 2. Если при х ® х₀ переменная х принимает только значения, меньшие х₀, и при этом функция f(x) стремится к некоторому числу А, то говорят об одностороннем пределе функции слева:

f(x) = A

Аналогично, при х ® х₀, х > х₀ говорят об одностороннем пределе функции справа, т.е:

f(x) = A

При этом если f(x) = f(x), то f(x) = A.

Функция a(x) называется бесконечно малой величиной при или при , если ее предел равен нулю:

a(x) = 0

Связь бесконечно малых величин с пределами функций определяется теоремами:

Теорема: Если f(x) = A, то функцию f(x) можно представить в виде суммы f(x) = A + a(x), где a(x) – бесконечно малая при х ® х₀ (¥).

Обратная теорема: Если функцию f(x) можно представить как сумму числа А и бесконечно малой a(x) при х ® х₀ (¥), то число А есть предел этой функции при х ® х₀ (¥), т.е.

f(x) = A

Свойства бесконечно малых величин:

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Замечание. Свойство 3 не рассматривает предел отношения двух бесконечно малых a(x) и b(x) из-за его неопределенности. Этот предел может быть равен нулю, числу А ¹ 0 или бесконечности ¥. В первом случае a(x) называется бесконечно малой более высокого порядкамалости чем b(x). Это записывается так: a(x) = o(b(x)) при х ® х₀ (¥), т.е. “a(x) есть о малое от b(x)”. Во втором случае a(x) и b(x) одного порядкамалости (“a(x) есть О большое от b(x)” или b (x) = O(a(x))). В третьем случае a(x) более низкого порядка малости чем b(x). При a(x) и b(x) называются эквивалентными и пишут a(x)»b(x).

Функция f(x) называется бесконечно большой величиной при х ® х₀, если для любого M > 0 найдется такое d > 0 (d (M)), что для всех x ¹ x_0, |х – x₀| < d будет верно: .

Свойства бесконечно больших величин:

1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3. Частное от деления бесконечно большой величины на функцию, имеющую предел в точке х₀, есть величина бесконечно большая.

Связь между бесконечно малыми и бесконечно большими величинами устанавливает следующая теорема:

Теорема: Если a(x) есть бесконечно малая при х ® х₀ (¥), то функция является бесконечно большой при х ® х₀ (¥). Обратно, если функция a(x) есть бесконечно большая при х ® х₀ (¥), то функция есть бесконечно малая при х ® х₀ (¥).