Построение двойственной задачи
Рассмотрим обобщенную формулировку двойственной задачи линейного программирования, которая применима к любой форме представления прямой задачи и основывается на следующих правилах.
1. Число переменных в двойственной задаче равно числу основных ограничений в прямой задаче.
2. Матрица коэффициентов системы ограничений двойственной задачи получается из матрицы коэффициентов основной системы ограничений прямой задачи путем транспонирования.
3. Система основных ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы основных ограничений прямой задачи.
4. Свободными членами системы ограничений двойственной задачи являются коэффициенты функции цели прямой задачи.
5. Двойственная задача решается на минимум, если целевая функция прямой задачи задается на максимум, и наоборот.
6. Коэффициентами функции цели двойственной задачи служат свободные члены системы ограничений прямой задачи.
7. Если переменная прямой задачи 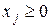 , то
, то 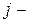 ое условие системы ограничений двойственной задачи является неравенством, если
ое условие системы ограничений двойственной задачи является неравенством, если 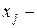 любое число, то
любое число, то 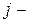 ое условие двойственной задачи представляет собой уравнение.
ое условие двойственной задачи представляет собой уравнение.
8. Если 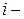 ое соотношение прямой задачи является неравенством, то соответствующая оценка
ое соотношение прямой задачи является неравенством, то соответствующая оценка 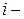 ого ресурса – переменная
ого ресурса – переменная 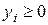 , если
, если 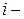 ое соотношение представляет собой уравнение, то переменная двойственной задачи
ое соотношение представляет собой уравнение, то переменная двойственной задачи 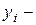 любое число.
любое число.
В качестве примера построения двойственной задачи для данной прямой задачи рассмотрим задачу рационального использования ресурсов, которая имеет вид:
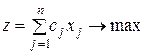 ,
,
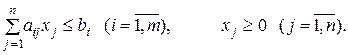
Необходимо найти план выпуска продукции 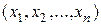 из имеющихся в наличии ресурсов
из имеющихся в наличии ресурсов 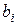 и нормативов затрат сырья на изготовление продукции, реализовав которую предприятие получит максимальную прибыль.
и нормативов затрат сырья на изготовление продукции, реализовав которую предприятие получит максимальную прибыль.
Выпишем теперь для этой задачи двойственную согласно рассмотренных выше правил составления двойственных задач.
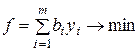 ,
,
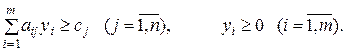
Здесь необходимо определить двойственную оценку единицы каждого вида ресурсов 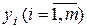 , чтобы при заданных объемах ресурсов
, чтобы при заданных объемах ресурсов 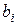 , прибыли
, прибыли 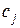 , нормах расхода ресурсов
, нормах расхода ресурсов 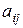 минимизировать оценку всех ресурсов предприятия, затраченных на выпуск произведенной продукции.
минимизировать оценку всех ресурсов предприятия, затраченных на выпуск произведенной продукции.
Система ограничений двойственной задачи показывает, что двойственная оценка всех ресурсов, затраченных на выпуск единицы продукции 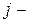 ого вида, должна быть не меньше прибыли, получаемой при реализации единицы продукции
ого вида, должна быть не меньше прибыли, получаемой при реализации единицы продукции 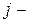 ого вида.
ого вида.
Решение прямой задачи дает оптимальные объемы выпуска продукции предприятием, а решение двойственной – оптимальную систему двойственных оценок ресурсов, используемых для изготовления производимой продукции.
Теоремы двойственности
Каждая из пары двойственных задач может быть решена самостоятельно. Однако, при определении оптимального плана одной из задач, находится решение другой.
Если 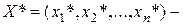 оптимальный план прямой задачи, а
оптимальный план прямой задачи, а 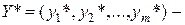 оптимальный план решения двойственной задачи, то
оптимальный план решения двойственной задачи, то
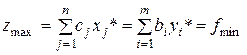 , (*)
, (*)
т.е. максимально возможная прибыль от реализации произведенной продукции, которая может быть получена при имеющихся запасах ресурсов, равна двойственной оценке этих ресурсов. Это утверждение известно под названием первой теоремы двойственности.
Оптимальный план прямой задачи можно записать в виде:
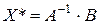 ,
,
где 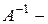 обратная матрица к матрице, составленной из компонент векторов, вошедших в оптимальный базис. Подставим оптимальный план прямой задачи в выражение (*):
обратная матрица к матрице, составленной из компонент векторов, вошедших в оптимальный базис. Подставим оптимальный план прямой задачи в выражение (*):
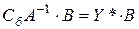 ,
,
где 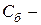 матрица коэффициентов базисных векторов, вошедших в оптимальный базис. Отсюда оптимальный план двойственной задачи равен:
матрица коэффициентов базисных векторов, вошедших в оптимальный базис. Отсюда оптимальный план двойственной задачи равен:
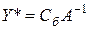 . (**)
. (**)
Таким образом, если найти оптимальный план прямой задачи, то, используя выражение (**), можно получить оптимальный план двойственной задачи. Компонентами этого плана являются элементы последней симплексной таблицы (содержащей оптимальный план прямой задачи), находящиеся на пересечении индексной строки и векторов, которые образовывали базис в первой симплексной таблице.
Очевидно, существует соответствие между переменными прямой и двойственной задач.
| Переменные прямой Задачи | основные 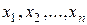 | дополнительные 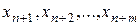 |
| Переменные двойственной Задачи | дополнительные 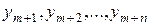 | основные 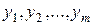 |
Согласно сопряженным парам переменных из решения прямой задачи можно получить решение двойственной, не решая ее, и, наоборот, из решения двойственной задачи – решение прямой.
Для оптимальных планов 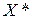 и
и 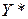 пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений:
пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений:
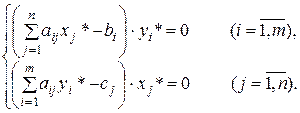
Вторая теорема двойственности, математически записанная выше системой уравнений, может быть интерпретирована следующим образом. Если в оптимальном плане некоторый 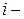 ый ресурс использован не полностью, то соответствующая оценка
ый ресурс использован не полностью, то соответствующая оценка 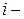 ого ресурса
ого ресурса 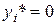 , т.е. если
, т.е. если 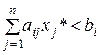 .
.
Таким образом, положительную двойственную оценку 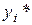 имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане, т.е.
имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане, т.е. 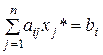 .
.
Вторая часть уравнений рассматриваемой системы свидетельствует о том, что реализации в оптимальном плане подлежат только те виды продукции 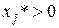 , для которых оценка затраченных на их производство ресурсов равна прибыли от их продажи, т.е. если
, для которых оценка затраченных на их производство ресурсов равна прибыли от их продажи, т.е. если 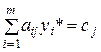 . Нецелесообразно реализовывать те виды продукции, для которых
. Нецелесообразно реализовывать те виды продукции, для которых 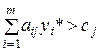 . В этом случае в оптимальном плане объем реализации данной продукции
. В этом случае в оптимальном плане объем реализации данной продукции 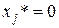 .
.
Пример.Составим двойственную задачу к прямой задаче планирования выпуска продукции, которая решена симплексным методом в 1.3.2. (стр. 23 – 25).
| Прямая задача | Двойственная задача |
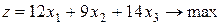 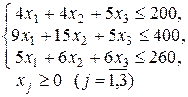 | 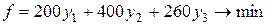 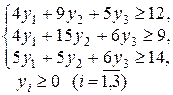 |
Эти задачи образуют симметричную пару двойственных задач. Решение прямой задачи дает оптимальный план выпуска продукции, а решение двойственной – оптимальную систему оценок ресурсов, используемых для ее изготовления.
Решение прямой задачи получено симплексным методом. Оптимальный план выпуска продукции:
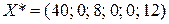 ,
, 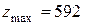 ден. ед.
ден. ед.
Используя последнюю итерацию прямой задачи (третья симплексная таблица ), найдем оптимальный план двойственной задачи.
Из первой теоремы двойственности следует, что 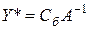 . Составим матрицу А из компонент векторов, входящих в оптимальный базис:
. Составим матрицу А из компонент векторов, входящих в оптимальный базис:
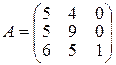 .
.
Определив каким-либо способом матрицу 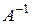 (например, с помощью алгебраических дополнений), получим:
(например, с помощью алгебраических дополнений), получим:
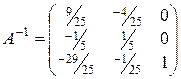 .
.
Как видно из третьей симплексной таблицы, элементы обратной матрицы 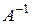 расположены в базисных столбцах первой симплексной таблицы
расположены в базисных столбцах первой симплексной таблицы 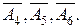
Тогда
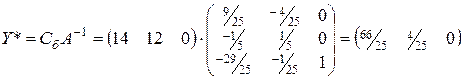 .
.
Это и есть оптимальный план двойственной задачи. При этом 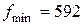 ден. ед.
ден. ед.
Подставим оптимальный план прямой задачи в систему ограничений математической модели планирования выпуска продукции
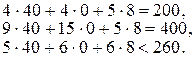
Первое и второе ограничения прямой задачи выполняются как равенства. Это означает, что ресурсы первого и второго видов полностью используются в оптимальном плане, являются дефицитными и их оценки согласно второй теоремы теории двойственности отличны от нуля 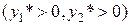 .
.
Третье ограничение выполняется как строгое неравенство, т.е. ресурс третьего вида израсходован не полностью, остаток его в оптимальном плане 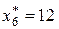 . Значит ресурс третьего вида не является дефицитным и оценка его в оптимальном плане двойственной задачи
. Значит ресурс третьего вида не является дефицитным и оценка его в оптимальном плане двойственной задачи 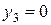 .
.
Таким образом, положительную двойственную оценку имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов.
При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:
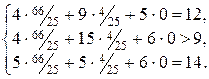
Первое и третье ограничения двойственной задачи выполняются как равенства. Это означает, что двойственные оценки ресурсов, используемых для изготовления единицы продукции первого и третьего видов, в точности равны прибыли, получаемой от реализации единицы соответствующего вида продукции. Значит реализовывать эти виды продукции экономически целесообразно и поэтому их изготовление предусмотрено оптимальным планом прямой задачи 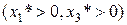 . Второе ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственные оценки ресурсов, используемых для производства единицы продукции второго вида выше прибыли, получаемой от реализации единицы продукции этого вида. Следовательно, изготовлять продукцию второго вида невыгодно и в оптимальном плане прямой задачи
. Второе ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственные оценки ресурсов, используемых для производства единицы продукции второго вида выше прибыли, получаемой от реализации единицы продукции этого вида. Следовательно, изготовлять продукцию второго вида невыгодно и в оптимальном плане прямой задачи 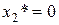 .
.
Величина двойственной оценки показывает: на сколько возрастет значение целевой функции при увеличении дефицитного ресурса на единицу. Например, увеличение первого вида ресурса на единицу приведет к получению нового оптимального плана, в котором прибыль возрастет на 2,64 ден. ед. и станет равной
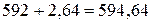 ден. ед.
ден. ед.
При этом коэффициенты оптимальной (третьей) симплексной таблицы столбца 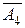 показывают, что указанное увеличение прибыли достигается за счет увеличения производства продукции третьего вида на величину
показывают, что указанное увеличение прибыли достигается за счет увеличения производства продукции третьего вида на величину 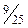 единицы, уменьшения объема производства первого вида продукции на величину
единицы, уменьшения объема производства первого вида продукции на величину 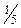 единицы и уменьшения остатка ресурса третьего вида на
единицы и уменьшения остатка ресурса третьего вида на 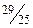 единицы.
единицы.
В то же время ввод в производство продукции второго вида (не вошедшей в оптимальный план) уменьшает прибыль предприятия. Если 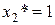 , то
, то
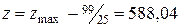 ден. ед.
ден. ед.
При этом коэффициенты оптимальной (третьей) симплексной таблицы столбца 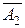 показывают, что указанное уменьшение прибыли происходит за счет уменьшения объема производства продукции третьего вида на величину
показывают, что указанное уменьшение прибыли происходит за счет уменьшения объема производства продукции третьего вида на величину 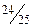 единицы, увеличения производства продукции первого вида на величину
единицы, увеличения производства продукции первого вида на величину 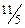 единицы и высвобождения ресурса третьего вида на
единицы и высвобождения ресурса третьего вида на 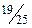 единицы.
единицы.
Таким образом, двойственные оценки связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных прямой задачи оказывает влияние на ее оптимальный план и на систему двойственных оценок. В свою очередь двойственные оценки служат инструментом анализа и принятия правильных решений в условиях меняющихся производственных ситуаций.
