Уравнения с отклоняющимся аргументом

Определение 1. Дифференциальным уравнением (ДУ) с отклоняющимся аргументом называется дифференциальное уравнение, в которое неизвестная функция и ее производные входят, вообще говоря, при различных значениях аргумента.

Например,

x ^/ (t) =f (t , x(t),x(t-t)) ,t>0 (1)

Впервые отдельные уравнения такого типа появились в литературе во второй половине 18 столетия (Кондорсе 1771), но систематическое изучение их началось лишь в 20 веке.

Основная начальная задача для уравнения (1) заключается в определении непрерывного решения x(t) уравнения (1) при t>t₀ при условии, что x(t)=j(t) при t-t£ t £ t₀, где j(t)- заданная непрерывная функция, называемая начальной.

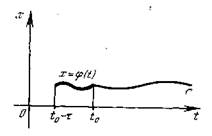Отрезок t₀-t£ t £ t₀, на котором задана начальная функция, называется начальным множеством и обозначается 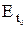; точка t₀ называется начальной точкой. Обычно предполагается, что

X (t₀+0)=j(t₀). (см. рис.1)

рис.1

Рассмотрим дифференциальное уравнение n-го порядка с L отклонениями аргумента,

,

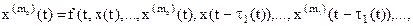
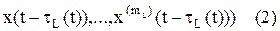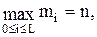где отклонения t_I(t)³0. Здесь под x^(k)(t-t_I(t)) понимается k-я производная от функции x(z), взятая в точке z = t-t_I(t). В дальнейшем предполагается, что все отклонения t_I(t) непрерывны.

Пусть уравнение (2) разрешимо относительно 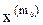(t); Обозначим l=m₀-m, где m=max .

.

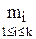Замечание.Уравнения, для которых l>0, называются уравнениями запаздывающего типа (у них старшая производная, входящая в уравнение, не содержит запаздывания). (ЗФДУ)

Уравнения, для которых l=0, называются уравнениями нейтрального типа (у них старшая производная входит в уравнение, как с запаздыванием, так и без него). (НФДУ)

Уравнения, для которых l<0, называются уравнениями опережающего типа (для них характерно, что старшая производная, входящая в ДУ, содержит запаздывание, а производная того же порядка без запаздывания отсутствует). (ОФДУ)

Отметим ещё, что естественная классификация уравнений с отклоняющимся аргументом была предложена Г.А.Каменским.

Примеры:

1)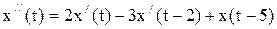 -ДУ запаздывающего типа.

2) 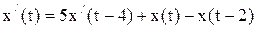-ДУ нейтрального типа.

3) 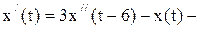ДУ опережающего типа.

Рассмотрим ДУ

x ^/ (t)=f (t, x (t), x (t-t)) (1)

с начальным условием x (t)= j(t), t 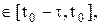где j(t)- начальная функция, 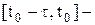начальное множество, t- запаздывание, t>0(запаздывание t может быть переменным: t=t(t)).

Основная начальная задача (задача Коши) для уравнения (1)заключается в нахождении непрерывного решения x(t), удовлетворяющего уравнению (1) с начальным условием x (t)= j(t), t .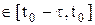

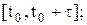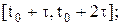
Наиболее естественным методом нахождения решения уравнения (1) является так называемый «метод шагов» (метод последовательного интегрирования ДУ на отрезках , 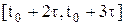и т. д.), заключающийся в том, что решение x(t) рассматриваемого уравнения определяется из дифференциального уравнения без запаздывания

x ^/(t)=f (t ,x (t),j₀(t-t)), t₀£ t £ t₀+t, x(t₀)=j₀(t₀),

так как при t₀£t£t₀+t аргумент t-t изменится на начальном множестве

[t₀-t;t₀] и, следовательно, третий аргумент x(t-t) функции f равен начальной функции j₀(t-t).

Предполагая существование решения x =j₁(t) этой начальной задачи на всем отрезке[t₀;t₀+t] , аналогично получаем:

x^/(t)= f(t,x(t),j₁(t-t)), при t₀+t £ t £ t₀+2t , x₀(t₀+t)=j₁(t₀+t)

………………………………………………………………..

x^/(t)= f(t, x(t),j_n(t-t)), при t₀+nt £ t £ t₀+(n+1)t, x₀(t₀+nt)=j_n(t₀+nt)

Пример 2.Для уравнения x(t)= 6x(t-1), x=t при 0 £ t £ 1 определить x(t) при 1<t£3.

Применяя метод шагов, получим: x^/(t)=6(t-1), 1 £ t £ 2, x(1)=1, так как x(1)=1 . Интегрируя, находим:

x(t)= 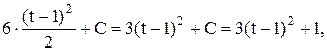(так как 1=3(1-1)²+С 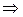С=1). При 2 £ t £3: x^/(t)=6 [3(t-2)²+1], x(2)=4, так как 3(2-1)²+1=4, тогда интегрируя: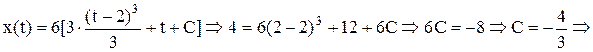

x(t)=6(t-2)²+6t-8.

Заметим, что даже в случае существования непрерывных производных от функций j и f сколь угодно высокого порядка решение основной начальной задачи будет, вообще говоря, иметь разрыв первого рода у производной порядка k в точке t₀+(k-1)t, но производные более низких порядков в этой точке будут уже непрерывны.

Действительно, в точке t₀ x^/(t) имеет, вообще говоря, разрыв первого рода, так как интегрируя уравнение

x^/(t)=f(t, x(t),j₀(t-t)), t₀ £ t £t₀+t, можно удовлетворить условию

x(t₀)=j₀(t₀),но, вообще говоря, нельзя удовлетворить, кроме того, условию

x^/(t₀+0)=j^/₀(t₀-0).

Таким образом, применение метода шагов становится затруднительным, если запаздывание t мало по сравнению с отрезком, на котором требуется определить решение.