Среди них есть хотя бы одно отрицательное;
Упражнения
5.1. Ячейки А20:Н20 заполнить словом «ячейка» (или каким-либо другим).
5.2. Ячейки А21:Н21 заполнить числом 762.
5.3. Ячейки А22:Н22 заполнить числами 88, 77, …
5.4. Ячейки А23:Н23 заполнить числами 2, 4, 8, 16, …
5.5. Ячейки А24:Н24 заполнить значениями геометрической прогрессии: первый член = 25, знаменатель = 0,4.
5.6. Ячейки А25:Н25 заполнить значениями Слон1, Слон2 и т.д.
5.7. Ячейки А26:Н26 заполнить значениями дат: янв.08, фев.08 и т.д.
5.8. Ячейки А28:Н28 заполнить значениями дат: янв.08, дек 07, ноя 07 …
Работа 6. Вычисления в таблицах
Вычисления в Excel выполняются с помощью формул. Формула начинается знаком «=» и состоит из операндов, соединенных операторами (знаками операций).
Операндами формул могут быть константы, ссылки на ячейки или диапазоны ячеек, функции.
Операторы – это:
- сложение (+);
- вычитание (-);
- умножение (*);
- деление (/);
- возведение в степень (^);
- круглые скобки ();
- меньше (<);
- меньше или равно (<=);
- равно (=);
- не равно (<>);
- больше или равно (>=);
- больше (>).
Функция состоит из имени, за которым в круглых скобках помещается список аргументов. У некоторых функций список аргументов может быть пустым.
Задание 6.1. Создать новую книгу Excel с именем «Вычисления». Примеры выполним на Листе 1.
Пример 6.1. Вычислить 23 + 6,5´4,2 .
Вариант 1. В ячейку А1 поместим формулу « =2^3+6,5*4,2».
После нажатия клавиши [ENTER] в ячейке будет результат вычисления (ответ: 35,3).
Вариант 2. Все числа, входящие в выражения, поместим в отдельные ячейки:
4 В ячейки В3:В6 поместим числа 2; 3; 6,5; 4,2 Þ в ячейку В7 поместим формулу «=B3^B4+B5*B6» Þ [ENTER].
4 Улучшим вид таблицы: в ячейки А3:А6 поместим разметку – названия переменных величин «a», «b», «c», «d» Þ в ячейку А7 поместим название результата: «y». Это соответствует вычислению по формуле
y=ab +cd.
4Меняя содержимое ячеек В3:В6, наблюдаем изменение результата расчета по формуле в ячейке В7.
Вариант 3. Поместим формулу в ячейку С7. При вводе формулы ссылки на ячейки будем формировать с помощью мыши, а не клавиатуры.
4 В ячейку С7 ввести знак «=» Þ щелкнуть в ячейке В3 (в строке формул появится ссылка на ячейку В3) Þ ввести знак «^» Þ щелкнуть в ячейке В4 Þ знак «+» Þ щелкнуть в ячейке В5 Þ знак «*» Þ щелкнуть в ячейке В6 Þ [ENTER].
В дальнейшей работе такой прием формирования ссылок на ячейки должен стать преобладающим.
Пример 6.2. Вычислить 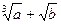 .
.
Вычисления выполним в столбце D. Значения a и b разместим в ячейках D3 и D4 соответственно.
4 В ячейку D7 поместим формулу «=D3^(1/3)+D4^(1/2)».
4 Для a и b задать значения (например, 27 и 16 соответственно). Сравнить полученный результат с ожидаемым.
4 Видоизменить формулу в ячейке D7, убрав круглые скобки.
Видим, что результат изменился. Причина – нарушение правила старшинства операций. Возведение в степень старше деления, поэтому выражение для дробной степени необходимо заключать в скобки.
Пример 6.3. Вычислить
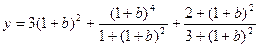 .
.
Можно, конечно, записать все одной формулой. Следует, однако, иметь в виду, что при размещении в одной ячейке достаточно длинной формулы теряется ее наглядность, и, как следствие, возрастает вероятность совершения ошибки.
Поступим следующим образом: отведем по отдельной ячейке для каждого из трех слагаемых, образующих формулу. Кроме того, проанализировав исходную формулу, видим, что в ней неоднократно встречается выражение (1+b)2. И для него выделим отдельную ячейку.
Пример разместим в столбцах G,H.
4В ячейку G3 поместим текст «b» Þ в ячейку G4 поместим текст «(1+b)2» Þ в ячейки G5:G7 поместим текст «1 слаг», «2 слаг», «3 слаг» соответственно и в ячейку G8 поместим текст «у».
4 В ячейку Н4 поместим формулу «=(1+H3)^2» Þ ячейку Н5 поместим формулу «=3*H4» Þ в ячейку Н6 поместим формулу «=H4^2/(1+H4)» Þв ячейку Н7 поместим формулу «=(2+H4)/(3+H4)».
4 В ячейку Н8 поместим окончательную формулу «=H5+H6+H7».
4 Произвести вычисления, изменяя значение b (содержимое ячейки Н3).
Упражнения
6.1. Вычислить 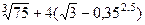 .
.
6.2. Вычислить 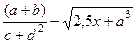 .
.
Значения a, b, c, d, x могут быть разные.
6.3. Вычислить площадь треугольника по трем сторонам.
6.4. Вычислить сторону куба, если задан его объем.
6.5. Для разных значений a, b вычислить
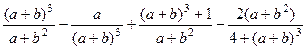 .
.
6.7. Вычислить радиус цилиндра, если заданы его объем и высота.
Работа 7. Функции
Функция -это заранее определенная формула, которая выполняет вычисления по заданным величинам, называемым аргументами.
Функция состоит из имени, за которым в круглых скобках следует список аргументов. Аргументы в списке отделяются друг от друга символом «;» – точка с запятой.
Необходимо следить за соответствием аргументов как по типу данных, так и по количеству.
Аргументами функций могут быть:
- константы;
- ссылки на ячейки или диапазоны ячеек;
- функции.
Некоторые функции не требуют аргументов, однако круглые скобки при этом все равно записываются.
Примеры функций:
| Функция | Аргумент |
| SIN(2) | Константа |
| КОРЕНЬ(А3) | Ссылка на ячейку А3 |
| СУММ(А1:Е55) | Ссылка на диапазон ячеек А1:Е55 |
| LN(А3*КОРЕНЬ(Е4)) | Выражение |
| ПИ() | Нет аргумента |
Задание 7.1. Для выполнения примеров Листу 2 книги «Вычисления» дать имя «Функции».
Пример7. 1. Вычислить 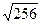 .
.
4 В ячейку В1 ввести формулу «=КОРЕНЬ(256)» Þ [ENTER].
Можно, конечно, использовать операцию возведения в степень (1/2), но для примера мы применили функцию КОРЕНЬ – извлечение квадратного корня.
Пример 7.2.Вычислить массу шара радиуса R, изготовленного из материала с удельной массой р.
Масса шара есть произведение его объема 4/3´pR3 на удельную массу материала. Для получения значения p будем использовать функцию ПИ().
4 Разметим ячейки А3, В3, С3 и D3 соответственно «радиус», «уд. масса», «объем», «масса».
4 В ячейку С4 поместим формулу «=4/3*ПИ()*A4^3» Þ в ячейку D4 формулу «=C4*B4» Þ [ENTER].
4 Изменяя содержимое ячеек А4, В4, выполнить расчет массы.
Не забыть произвести оформление блока ячеек данного примера.
Пример 7.3.Вычислить значения тригонометрических функций sin, cos, tg, ctg. Аргумент задавать в градусах.
Прежде, чем выполнять вычисления, обратим внимание на следующее:
1) аргумент для тригонометрических функций Excel должен быть задан в радианах, поэтому если исходные значения нам удобнее задавать в градусах, то их нужно предварительно перевести в радианы либо по формуле
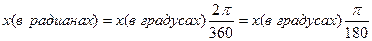 ,
,
либо применить функцию преобразования РАДИАНЫ (угол в градусах);
2) В Excel нет функции ctg, поэтому для ее вычисления придется использовать либо выражение 1/ tg, либо cos /sin.
Пример выполним на листе «Функции» книги «Вычисления».
4 Ячейки A8:F8 разметим так: «x, град», «х, рад», «sinx», «cosx», «tgx», «ctgx».
4 В ячейку В9 поместим формулу «=A9*ПИ()/180» – перевод градусов в радианы Þ в ячейки C8:F8 соответственно поместим формулы «=SIN(B9)», «=COS(B9)», «=TAN(B9)», «=D9/ C9».
4Задавая значение х (содержимое ячейки А9), получим значения функций.
Пример 7.4.Вычислить 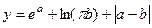 .
.
4 В ячейки А13, В13, С13 введем разметку переменных: «a», «b», «y».
4 В ячейку С14 поместим формулу «=EXP(A14)+LN(ПИ()*B14)+ABS(A14-B14)» (для вычисления модуля – абсолютного значения разности a-b используется функция ABS).
4 Изменяя значения a и b, наблюдать изменение значения у.
Упражнения
7.1. Вычислить 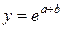 (например, при a=0,25; b=0,75 y=2,718281828…).
(например, при a=0,25; b=0,75 y=2,718281828…).
7.2. Вычислить 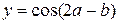 . Аргумент функции cos задавать в градусах (например, при a=45; b=30 получим y=0,5).
. Аргумент функции cos задавать в градусах (например, при a=45; b=30 получим y=0,5).
7.3. Вычислить 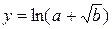 (например, при a=1; b=4 получим y=1,098612289…).
(например, при a=1; b=4 получим y=1,098612289…).
Работа 8. Ошибки в формулах
Нередко при выполнении расчетов в ячейке с формулой вместо результата появляется сообщение об ошибке. Признаком ошибки является знак «#», за которым следует текст, определяющий тип ошибки. Ниже приведены некоторые ошибки и способы их устранения.
| Тип ошибки | Причина ошибки | Способ устранения |
| ####### | Недостаточно места для размещения результата вычисления по формуле | Расширить столбец, в котором размещается результат |
| #ЗНАЧ! | Аргумент функции недопустимого типа | Проверить правильность написания аргументов функций и содержимое ячеек, на которые есть ссылки в формуле, на соответствие типов данных |
| #ДЕЛ/0! | Деление на ноль | Проверить правильность написания формулы и содержимое ячеек, на которые есть ссылки |
| #ИМЯ? | Excel не может найти функцию или диапазон ячеек с заданным именем | Проверить правильность написания имен функций и диапазонов ячеек (особенно применение русского и английского алфавитов) |
| #ЧИСЛО! | Недопустимое числовое значение в формуле или функции | Проверить формулу на правильность задания математических операций и возможность выхода результата за допустимые пределы представления чисел |
В приводимых ниже примерах мы будем искусственно создавать ситуации с ошибками.
Задание 8.1. Для выполнения примеров Листу 3 книги «Вычисления» дать имя «Ошибки».
Пример 8.1. Вычислить y=ln(a+b).
4 Разметить ячейки А3:С3 «a», «b», «y» соответственно Þ в ячейку С4 ввести формулу «=LN(A4+B4)» Þ [ENTER].
4 Щелкнуть мышью в ячейке с ошибкой (С4) Þ навести указатель мыши на появившуюся рядом кнопку с восклицательным знаком Þ щелкнуть на появившуюся кнопку [6] раскрытия списка.
В первой строке указан тип ошибки. Вторая строка списка позволяет обратиться к справке по данной ошибке. Правда, рекомендации, изложенные в справке, обычно носят общий характер. В нашем случае не заданы значения a и b (ячейки А4, В4), поэтому делается попытка вычислить ln(0), что невозможно.
4 Задать числовые значения a и b (например, 1 и 2). Ошибка должна исчезнуть.
4 В ячейку А4 запишем какую-нибудь букву Þ проанализируем ошибку #ЗНАЧ! Þ исправим ошибку.
Пример 8.2. Вычислить ex .
4 Разметим ячейки А7, В7 «х», «y» соответственно Þ в ячейку В8 введем формулу «=EXP(A8)».
4 Зададим значение х=1000 Þ изучим справку по ошибке #ЧИСЛО! (нам важна третья причина: выход результата за допустимые пределы).
4 Изменяя х, найти то максимальное значение, при котором возможно вычисление по формуле.
Пример 8.3. Вычислить 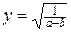 .
.
4 Разметим ячейки А12:С12 «a», «b», «y» соответственно Þ в ячейку С13 ввести формулу «=КОРЕНЬ(1/(A13-B13))» Þ [ENTER].
Если не были заданы значения a, b, получим ошибку #ДЕЛ/0!
4 Изучить справку по ошибке Þ задать допустимые данные.
4 Внести изменение в название функции КОРЕНЬ (например, русскую букву «К» заменить на английскую) Þ изучить справку по ошибке #ИМЯ?
4 Внести исправление в формулу.
4 Зададим, например, a=3, b=1 Þ уменьшая размер столбца с результатом (столбца С), наблюдать отображение в нем результата вычислений (происходит округление).
Пример 8.4.
4В примере 8.2. зададим х=100 Þ уменьшать размер столбца «В», пока в ячейке результата (В8) не появится ошибка #### Þ исправить ошибку.
В этом примере при уменьшении ширины столбца сначала происходит округление, а потом, когда уже не хватает места для представления числа в экспоненциальном формате, возникает ошибка.
Работа 9. Мастер функций
Мастер функций – это инструмент, позволяющий быстро найти и вставить в формулу нужную функцию. При этом можно получить достаточно полную справку по интересующей нас функции.
Задание 9.1. В книгу «Вычисления» добавить лист с именем «Мастер функций». На этом листе будем выполнять примеры и упражнения этой темы.
Пример 9.1. Вычислить 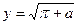 .
.
Можно, конечно, сразу записать формулу для вычисления выражения, но продемонстрируем, как можно использовать инструмент Мастер функций.
4 Открыть книгу «Вычисления» Þ активировать лист «Мастер функций».
4 В ячейки А3 и В3 поместим разметку: «a», «y».
4 Выделить ячейку для вставки формулы (В4) Þ на панели инструментов нажать кнопку fx – вставка функции.
На экране появится окно Мастер функций. В раскрывающемся списке Категория нужно выбрать категорию, к которой относится нужная нам функция, а затем в списке «Выберите функцию» выделить нужную функцию. При выделении функции под панелью «Выберите функцию» приводится синтаксис функции (правила обращения к ней).
Для получения детальной справки по выбранной функции следует щелкнуть гиперссылку [Справка по этой функции] в левом нижнем углу окна Мастер функций.
Итак, продолжаем:
4 Поищем функцию КОРЕНЬ в категории Математические, или, если не знаем категории, в полном алфавитном перечне Þ выделить функцию КОРЕНЬ Þ [ОК].
На экране появится окно Аргументы функции. Для получения детальной справки по выбранной функции следует щелкнуть гиперссылку [Справка по этой функции] в левом нижнем углу окна Мастер функций.
4 Вызвать справку по выбранной функции Þ после изучения справки закрыть окно справки.
В окне Аргументы функции в строке ввода Число необходимо задать аргумент функции:
4в строке Число ввести «ПИ()+» Þ щелкнуть в ячейке А4 (это будет ссылка на ячейку) Þ [ОК].
4Изменяя содержимое ячейки А12, наблюдать изменение результата.
Пример 9.2. Вычислить 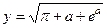 . Результат поместить в ту же ячейку (В4), что и в предыдущем задании.
. Результат поместить в ту же ячейку (В4), что и в предыдущем задании.
Можно, конечно, ввести формулу заново, но мы для разнообразия просто отредактируем прежнюю формулу.
4 Выделить ячейку с редактируемой формулой (В4) Þ в строке формул установить курсор мыши в место вставки дополнительного слагаемого Þ ввести знак «+» Þ слева от строки формул раскрыть список используемых функций (нажать кнопку [6]) Þ в раскрывшемся списке выбрать функцию ЕХР Þ в окне Аргументы функции в строке Число задать ссылку на ячейку с аргументом а (либо с клавиатуры ввести «А4», либо щелкнуть мышью в этой ячейке) Þ [ОК].
Упражнения
9.1. Вычислить 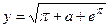 .
.
9.2. Вычислить 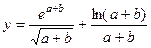 .
.
9.3. Вычислить площадь круга при заданном диаметре.
9.4. Вычислить радиус круга, если задана площадь.
9.5. Преобразовать целое число в римскую систему (найти функцию РИМСКОЕ, изучить справку);
9.6. По заданной дате (число, месяц, год) определить день недели (отыскать нужную функцию в категории Дата и время).
Работа 10. Логические функции
Логические величины могут принимать лишь 2 значения: ЛОЖЬ (FALSE) и ИСТИНА (TRUE).
В Excel в категорию логических включены следующие функции: ЛОЖЬ, ИСТИНА, НЕ, И, ИЛИ, ЕСЛИ.
Логические функции (за исключением функции ЕСЛИ, которая в математическом смысле не относится к логическим) в качестве параметров (аргументов) имеют логические величины и в качестве результата возвращают значения логического типа. Функции ЕСЛИ более подробно посвящена следующая работа.
Функции ЛОЖЬ и ИСТИНА не имеют аргументов и служат для задания соответствующих логических величин. Могут записываться как со скобками (ЛОЖЬ(), ИСТИНА()), так и без них.
Функция НЕ может иметь лишь один аргумент. Она изменяет его значение на противоположное (ЛОЖЬ на ИСТИНА, ИСТИНА на ЛОЖЬ).
Функция И может иметь любое количество аргументов. Результатом является ИСТИНА, если все аргументы одновременно имеют значение ИСТИНА, в противном случае результатом является ЛОЖЬ.
Функция ИЛИ может иметь любое количество аргументов. Результатом является ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА, в противном случае результатом является ЛОЖЬ.
Логические значения получаются либо как результат выполнения операций сравнения (<; <=; <>; =; >=; >), либо как результат, возвращаемый функцией. Заметим, что в Excel кроме логических имеется еще ряд функций, возвращающих результат логического типа.
Задание 10.1. В книгу «Вычисления» добавить лист с именем «Логические Функции». На этом листе будем выполнять примеры и упражнения этой работы.
Пример 10.1. Имеется 2 числа: a и b. Составить логические выражения, с помощью которых можно проверить истинность утверждений:
· a > b;
· a = b;
· a ³ b;
Это пример на использование логической функции «И».
Создадим такую таблицу:
| a | b | a > b | a = b | a ³ b |
Значения a, b будем задавать, значения других столбцов будем рассчитывать. Итак:
4 Открыть книгу «Вычисления», лист «Логические Функции».
4 Создать таблицу, вводя названия столбцов, начиная с ячейки В3.
4 В ячейку D4 введем формулу «=B4>C4», в ячейку Е4 – формулу «=B4=C4» и в ячейку F4 – формулу «=B4>=C4».
4 Изменяя значения a и b, наблюдать и анализировать изменение результата.
Пример 10.2. Имеется 3 числа: a, b, с. Составить логические выражения, с помощью которых можно проверить истинность утверждений:
· a, b, c – все положительные;
· a < b < c;
Одновременно: .
Это пример на использование логической функции «И». Создадим таблицу:
| a | b | c | все положительные | a < b < c | 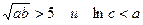 |
Значения a, b, c будем задавать, значения других столбцов будем рассчитывать.
4 Открыть книгу «Вычисления», лист «Логические Функции».
4 Создать таблицу, вводя названия столбцов начиная с ячейки В8.
В ячейку Е9 надо ввести формулу «=И(B9>=0;C9>=0;D9>=0)». Сделаем это так:
4 Выделить ячейку Е9 Þ на панели инструментов нажать кнопку fx – вставка функции Þ в окне Мастер функций в категории Логические выбрать функцию «И» Þ [ОК].
4 В окне Аргументы функции установить курсор мыши в строке Логическое_значение1 Þ щелкнуть в ячейке В9 Þ набрать на клавиатуре «>=0» Þ в окне Аргументы функции установить курсор мыши в строке Логическое_значение2 Þ ввести выражение «C9>=0» Þ в окне Аргументы функции установить курсор мыши в строке Логическое_значение3 Þ ввести выражение «D9>=0» Þ [ОК].
Для проверки комбинированного условия a < b < c необходимо проверить одновременное выполнение двух условий: a < b и b < c (именно так!):
4 В ячейку F9 ввести формулу «=И(B9<C9;C9<D9)» (конечно же, рекомендуется использовать Мастер функций).
И, наконец:
4 В ячейку G9 ввести формулу «=И(КОРЕНЬ(B9*C9)>5;LN(D9)<B9)».
Изменяя значения a, b, c, наблюдать и анализировать изменение результата.
Пример 10.3. Имеется 3 числа: a, b, с. Составить логические выражения, с помощью которых можно проверить истинность утверждений:
среди них есть хотя бы одно отрицательное;
