Гидродинамика. Линии тока. Уравнение Бернулли.

Гидродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа. Как и в других разделах физики сплошных сред, прежде всего, осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

Идеальная среда

С точки зрения механики, жидкостью называется вещество, в котором в равновесии отсутствуют касательные напряжения. Если движение жидкости не содержит резких градиентов скорости, то касательными напряжениями и вызываемым ими трением можно пренебречь и при описании течения. Если вдобавок малы градиенты температуры, то можно пренебречь и теплопроводностью, что и составляет приближение идеальной жидкости. В идеальной жидкости, таким образом, рассматриваются только нормальные напряжения, которые описываются давлением. В изотропной жидкости, давление одинаково по всем направлениям и описывается скалярной функцией.

Линии тока

1) векторного поля р, линии, в каждой точке которых касательная имеет направление вектора поля в этой точке. Дифференциальные уравнения Л. т. имеют вид:

dx/p₁ = dy/p₂ = dz/p₃,

где p₁, p₂, p₃ — координаты вектора поля, а х, у, z — координаты точки Л. т.

2) В гидроаэромеханике, линия, в каждой точке которой касательная к ней совпадает по направлению со скоростью частицы жидкости в данный момент времени. Совокупность Л. т. позволяет наглядно представить в каждый данный момент времени поток жидкости, давая как бы моментальный фотографический снимок течения. Они могут быть сделаны видимыми с помощью взвешенных частиц, внесённых в поток (например, алюминиевый порошок в воде, дым в воздухе)

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

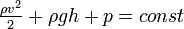
Здесь

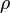— плотность жидкости,

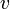— скорость потока,

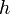— высота, на которой находится рассматриваемый элемент жидкости,

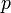— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

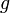— ускорение свободного падения.

Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.

Это соотношение, выведенное Даниилом Бернулли в 1738 г., было названо в его честь уравнением Бернулли.

Для горизонтальной трубы h = 0 и уравнение Бернулли принимает вид: .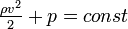

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности ρ: .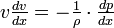

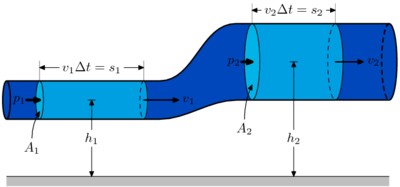
Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из гидростатического (ρgh), атмосферного (p) и динамического 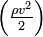давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы.