Минор и алгебраическое дополнение.
Раздел 2 ЛИНЕЙНАЯ АЛГЕБРА
Тема 2.1 Матрицы и определители
Таблица, состоящая из 
строк и 
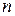столбцов, называется матрицей размерности 
:
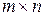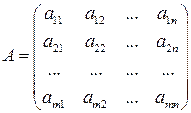, (2.1)
где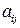 
– элементы матрицы ( 
; 
).
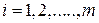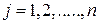Сокращенная запись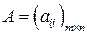 
или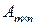 
.
Если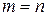 
, то матрица называется квадратной. В этом случае число 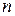называется ее порядком. В квадратной матрице n-го порядка диагональ, состоящая из элементов 
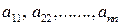,называется главной диагональю.
Две матрицы 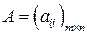и 
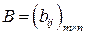одинаковой размерности называются равными, если все их соответствующие элементы равны.
Действия над матрицами
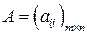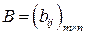Суммой (разностью) двух матриц и одинаковой размерности называется матрица 
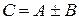, элементы которой определяются равенством
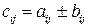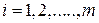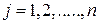( ; ) (2.2)
Произведением матрицы 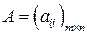на число 
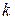называется матрица 
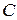, каждый элемент которой равен произведению соответствующего элемента матрицы 
на число :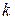
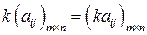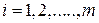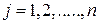( ; ). (2.3)
Произведением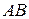
матрицы 
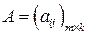на матрицу 
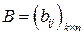называется матрица 
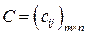, элемент 
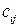которой равен сумме произведений элементов i-й строки матрицы на соответствующие элементы j-го столбца матрицы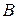 
, т.е.
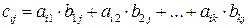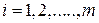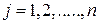, ( ; ) (2.4)
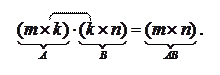Произведение матрицы на матрицу 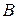определено только в том случае, когда число столбцов первого множителя (матрицы ) равно числу строк второго множителя (матрицы 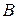). При этом размерность матрицы 
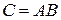равна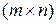 
:
Матрица, полученная из матрицы заменой всех строк соответствующими по номеру столбцами, называется транспонированной по отношению к матрице и обозначается 
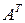или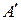 
, т.е.
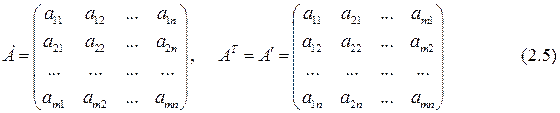
Определители
Каждой квадратной матрице по определенному закону ставится в соответствие некоторое число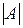 
, называемое определителем (детерминантом) этой матрицы. Обозначают определители так:
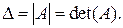
Определителем второго порядка называется число, записанное в виде таблицы и равное
.
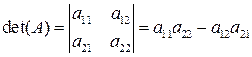Например,
.
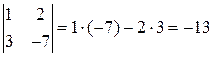Определителем 3-го порядка называется число, равное
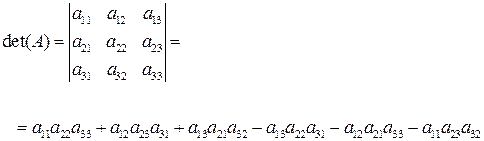(2.6)
Каждое слагаемое равно произведению трех элементов, взятых по одному из каждого столбца и каждой строки, число слагаемых при этом равно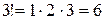 
.
Определитель 3-го порядка можно вычислить по правилу треугольника (правилу Саррюса). Если соединить линией каждые три элемента определителя (по одному из каждой строки и каждого столбца), то получим легко запоминающуюся схему:
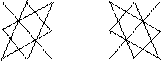D =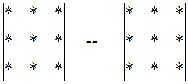 
.
На левой схеме линиями соединены каждые три элемента определителя, произведение которых входит в определитель со знаком “+”, на правой схеме приведены произведения, которые входят в определитель со знаком “–”.
Определителем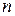-го порядка ( 
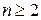) называется число, записанное в виде таблицы, состоящей из 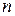строк и 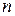столбцов:
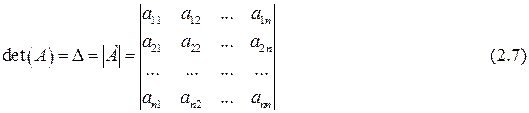
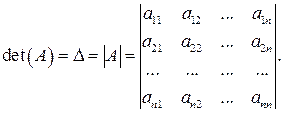 | (2.7) |
Основные свойства определителей
1. При транспонировании матрицы величина ее определителя не изменяется.
2. Если поменять местами любые две строки или два столбца, то определитель изменит свой знак на противоположный.
3. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
4. Если одна строка (столбец) определителя состоит только из нулей, то определитель равен нулю.
5. Определитель равен нулю, если имеются две одинаковые или две пропорциональные строки (столбца).
6. Величина определителя не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
7. Если элементы некоторой строки определителя представлены в виде суммы двух слагаемых, то определитель можно представить в виде суммы двух определителей D1 и D2. В определителе D1 указанная строка состоит из первых слагаемых, в определителе D2 – из вторых слагаемых. Остальные строки определителей те же, что и в исходном определителе.
Минор и алгебраическое дополнение.