Задания для самостоятельной работы. 1. Определите (приближенно), чему равна величина направленного угла (рис

1. Определите (приближенно), чему равна величина направленного угла (рис. 47, а, б).

2. Может ли величина направленного угла между векторами быть равна ? ? ? Почему?

3. Найдите формулы преобразования прямоугольной системы координат, если координатные векторы повернуты на угол , а начало координат перенесено в точку .

4. Как по формулам преобразования координат узнать, какая система координат подвергается преобразованию: аффинная или прямоугольная?

5. Сделайте чертежи старой и новой систем координат для частных случаев преобразования прямоугольной декартовой системы координат.

Полярные координаты

Если указано правило, по которому положение точек плоскости можно определить с помощью упорядоченных пар действительных чисел, то говорят, что на плоскости задана система координат. Кроме аффинной системы координат, которая была рассмотрена в §10, в математике часто применяют полярную систему координат на плоскости.

Система полярных координат вводится на ориентированной плоскости.

Пара, состоящая из точки О и единичного вектора 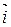, называется полярной системой координат и обозначается или . Направленная прямая называется полярной осью, точка О - полюсом (рис. 48).

О

Пусть М – произвольная точка плоскости. Расстояние от точки О до точки М называется полярным радиусом точки М.

.

Таким образом, . Если М совпадает с О, то . Для любой точки М ее полярный радиус

Направленный угол называется полярным углом точки М (рис. 49).

.

Если М совпадает с полюсом О, то j - неопределенный. Из определения направленного угла между векторами (см. §13) следует, что полярный угол

Полярный радиус r и полярный угол j называются полярными координатами точки М.

На рис. 50 построены точки , , по их полярным координатам.

Выведем формулы перехода от полярных координат к прямоугольным декартовым и обратно.

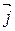Пусть - полярная система координат на ориентированной плоскости, , в . Присоединим к полярной системе единичный вектор , ортогональный вектору 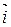так, чтобы базис 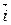, 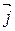был правым (рис. 51).

, .

Пусть М(х;у) в 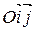. Тогда ; (рис. 51).

Получили формулы перехода от полярных координат к прямоугольным:

Возведем обе части этих равенств в квадрат и сложим:

, откуда (корень берется со знаком «+», т.к. ). Þ Þ ; .

, , .

Получили формулы перехода от прямоугольных декартовых координат к полярным:

Замечание. При решении задач на переход от прямоугольных декартовых координат к полярным недостаточно найти только или только , т.к. по одной тригонометрической функции определить полярный угол однозначно невозможно: в промежутке существуют два угла с одинаковыми косинусами (два угла с одинаковыми синусами) (рис. 52). Поэтому правильно найти полярный угол j вы сможете, только если одновременно вычислите и .