Свойства операций над множествами
1. Идемпотентность пересечения, объединения.
А 
А = А А 
А = А
2. Коммутативность пересечения, объединения.
А В = В А А В = В А
3. Ассоциативность пересечения, объединения.
(А В) С = А (В С) (А В) С = А (В С)
4. Законы поглощения.
(А В) А = А (А В) A = А
5. Свойства пустого множества.
А 
= А = А
6. Свойства универсума.
А U = A А U = U
7. Инволютивность.
= А
8. Законы де Моргана.
9. Свойства дополнения.
А 
= А = U
10. Выражения для разности.
А \ В = А 
1.2.Отношения.
Упорядоченные пары.
Если a и b – объекты, то через (a,b) обозначим упорядоченную пару. Равенство упорядоченных пар определяется следующим образом:
(a, b) = (c, d) 
a=с и b=d.
Т. е. (a, b)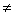 
(b, a), если a 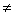b.
Пример: (3,4) 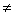(4,3).
Прямое произведение множеств.
Пусть A и B – два множества. Прямым (декартовым) произведением двух множеств A и B называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит A, а второй принадлежит B.
A 
B = {(a, b) | a 
A, b B}.
Пример: точка на плоскости может быть задана упорядоченной парой координат, т.е. двумя точками на координатных осях. Т.о., R2 = R R. Метод координат ввел в употребление Рене Декарт (1596 - 1650), отсюда и название – «декартово произведение».
Степенью множества А называется его прямое произведение самого на себя.
An = 
Соответственно, A1 = A, A2 = A A и вообще An = A An-1.
Теорема: |A B| = |A| |B|.
Доказательство: первый компонент упорядоченной пары можно выбрать |А| способами, второй - |B| способами. Таким образом, всего имеется |A| |B| различных упорядоченных пар.
Следствие: |An| = |A|n.
Комбинаторика
2.1.Введение
При решении многих практических задач приходится выбирать из некоторой совокупности объектов элементы, обладающие тем или иным свойством, подсчитать число различных комбинаций и т.п. Такие задачи называются комбинаторными, а раздел математики, занимающийся такого рода задачами, называется комбинаторикой.
Рассмотрим элементарный жизненный пример.
Пусть некоторое агентство недвижимости располагает базой данных из n записей, каждая запись содержит одно предложение (что имеется) и один запрос (что требуется). Требуется найти все такие пары записей, в которых предложение первой записи совпадает с запросом второй (осуществить подбор вариантов обмена). Допустим, что используемая СУБД позволяет проверить вариант за одну миллисекунду. При «лобовом» алгоритме поиска вариантов (каждая запись сравнивается с каждой) потребуется n(n-1)/2 сравнений. Если n=100, то ответ будет получен через 4,95 секунд; но если n=100000, то ответ будет получен за 4 999 950 секунд, что составляет почти 1389 часов и вряд ли это может считаться приемлемым. При этом мы оценили только трудоемкость прямых вариантов, но есть варианты, когда число участников сделки больше двух …
Этот пример показывает, что комбинаторные вычисления помогают осуществить предварительный анализ и количественную оценку исходных задач и используемых алгоритмов. Основным инструментом такого анализа являются законы и формулы комбинаторики.
2.2.Основные законы комбинаторики.
Правило суммы.
Задача: на блюде лежат 5 яблок и 2 груши. Сколькими способами можно выбрать один плод?
Решение: плод можно выбрать семью способами (5+2=7).
Если некоторый элемент a может быть выбран из множества элементов m способами, а другой элемент b может быть выбран n способами, причем любой выбор элемента b отличен от любого выбора элемента a, то выбрать либо a, либо b можно m + n способами.
На языке теории множеств это правило формулируется следующим образом:
Теорема1: если пересечение конечных множеств пусто, то число элементов в их объединении равно сумме чисел элементов множеств А и В.
А В = 
| А В | = |A| + |B|
Разберем случай, когда множества могут иметь непустые пересечения.
Теорема2: для любых конечных множеств верно равенство:
| А В | = |A| + |B| - | А В |.
Задача: среди студентов первого курса 30 человек имеют дома компьютер, 35 – учебник по информатике; оказалось, что 10 студентов имеют и компьютер, и учебник по информатике. Сколько студентов на первом курсе?
Решение: пусть множество А составляют студенты, имеющие компьютер, множество В – студенты, имеющие учебник по информатике; по условию задачи:
|A| = 30 |B| = 35 | А В | = 10 | А В | =?
| А В | = |A| + |B| - | А В | = 30 + 35 – 10 = 55.
Правило произведения.
Вторым основным правилом комбинаторики является правило произведения.
Задача: определить количество клеток в игре «морской бой», если номер клетки состоит из буквы (букв 10) и цифры (цифр тоже 10).
Решение: количество клеток равно 10•10=100.
Если элемент a можно выбрать из множества элементов m способами и после каждого такого выбора элемент bможно выбрать n способами, то два элемента (упорядоченную пару) a и b можно выбрать m•n способами.
На языке множеств это правило выражается в виде следующей теоремы.
Теорема3: если множества А и В конечны, то |A B| = |A| • |B|.
Следствие: если множества А1, А2, …, Аn - конечны, то
|A1 … Аn| = |A1|• … •|An|.
Задача: сколько номеров, состоящих из двух букв, за которыми идут три цифры можно составить, если использовать 29 букв и 10 цифр.
Решение: обозначим множество букв А, множество цифр – В; каждый номер требуемого вида является набором длины n из декартова произведения А А В В В; по условию |А| = 29, |В| = 10, тогда по следствию из теоремы3 имеем:
| А А В В В | = 29•29•10•10•10 = 841 000.
2.3.Формулы комбинаторики
Перестановки