Метод составления характеристического уравнения

Этот метод применим к нахождению решений систем линейных однородных дифференциальных уравнений с постоянными коэффициентами вида

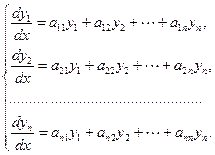(5)

Будем искать частное решение системы (5) в виде

,

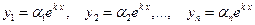где 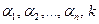- постоянные, подлежащие нахождению при решении системы уравнений. Подставив указанные выше функции 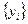в систему (5) и сократив на функцию 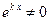, получим

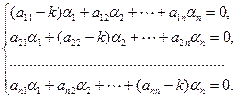(6)

Эта система линейных алгебраических уравнений относительно неизвестных 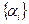имеет нетривиальное решение тогда и только тогда, когда

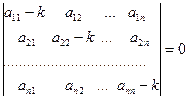. (7)

Уравнение (7) называется характеристическим уравнением системы (5).

Для каждого корня этого характеристического уравнения находим свой набор коэффициентов 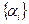, определяющий фундаментальное решение системы (5). После нахождения всех фундаментальных решений, можно построить общее решение рассматриваемой системы.

Преобразование Лапласа и его основные свойства, поиск изображения по оригиналу и оригинала по изображению, решение дифференциальных уравнений и их систем операционным методом.

I.Определения. Преобразованием Лапласа называется интегральное преобразование вида

,

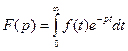где 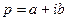- комплексное число ( 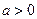), 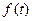- функция, удовлетворяющая условиям:

1) 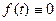при ;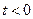

2) 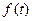- кусочно-непрерывная при ;

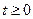3) существуют такие числа 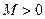и 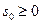, что для всех 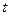выполняется неравенство 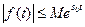(число 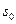называется показателем роста функции ).

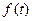Функция 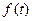называется оригиналом, а функция 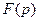- изображением оригинала 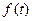. Соответствие между оригиналом и изображением записывают в виде 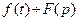или .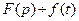

Теорема (о существовании изображения). Для всякого оригинала 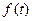изображение 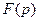существует в полуплоскости 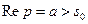, причем функция 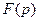является аналитической в этой полуплоскости.

Теорема (о единственности оригинала). Если функция 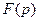является изображением двух оригиналов 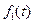и 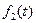, то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.

II.Свойства преобразования Лапласа.

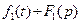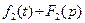1. Линейность. Если и , то .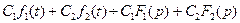

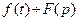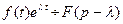2. Смещение (затухание). Если , то , где 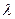- постоянная величина.

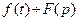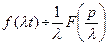3. Изменение масштаба (подобие). Если , то , где 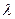- положительное число.

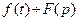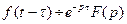4. Запаздывание. Если , то , где 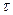- положительная величина.

5. Дифференцирование изображения. Если 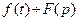, то .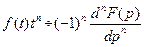

6. Дифференцирование оригинала. Если 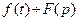, то .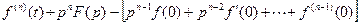

7. Интегрирование изображения. Если 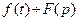и интеграл 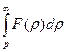сходится, то .

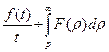8. Интегрирование оригинала. Если 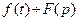, то .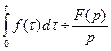

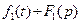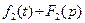9. Умножение изображений. Если и , то 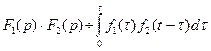. Интеграл 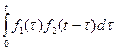называется сверткой функци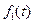й и 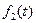, обозначаемой символом 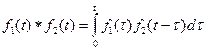. Свертка обладает свойством коммутативности: .

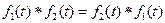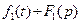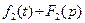10. Умножение оригиналов. Если и , то 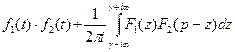, где путь интегрирования – вертикальная прямая .

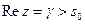III.

Таблица основных оригиналов и изображений

№	Оригинал	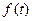Изображение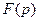
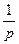	А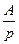
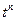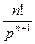
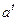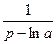
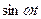
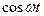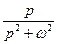
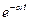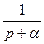
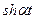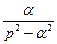
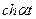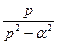
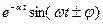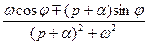
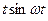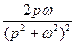
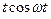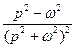