Методы интегрирования
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Наименование работы: ИНТЕГРИРОВАНИЕ ЗАМЕНОЙ ПЕРЕМЕННОЙ И ПО ЧАСТЯМ В НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск
2012 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ(2 курс)
Наименование работы: ИНТЕГРИРОВАНИЕ ЗАМЕНОЙ ПЕРЕМЕННОЙ И ПО ЧАСТЯМ В НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ.
1. Цель работы:Приобретение навыков интегрирования заменой переменной и по частям в определенном интеграле.
2. Литература:
2.1. В.А. Подольский, А.М. Суходольский "Сборник задач по математике" гл.11 §1-7 М.: Высшая школа, 1978 г.
2.2. Г.М. Гусак, Д.А. Капуцкая “Математика для подготовительных курсов” гл.10 §4-6 Минск: Высшая школа, 1989 г.
3. Подготовка к работе:
3.1. Изучить теоретический материал по теме: «Интегрирование заменой переменной и по частям в неопределенном интеграле».
3.2. Подготовить бланк отчета по практической работе.
3.3. Подготовить ответы на вопросы допуска к работе:
3.3.1. Понятие первообразной.
3.3.2. Понятие неопределенного интеграла.
3.3.3. Свойства неопределенного интеграла.
3.3.4. Формула интегрирования заменой переменной.
3.3.5. Формула интегрирования по частям.
4. Основное оборудование:
4.1. Литература, конспект.
5. Задание:
5.1. Вычислить неопределенные интегралы.
6. Порядок выполнения работы:
6.1. Записать задание своего варианта в отчет.
6.2. Выполнить интегрирование функции заменой переменной и по частям в неопределенном интеграле.
6.3. Записать ответы, оформить отчет.
6.4. Подготовить ответы на контрольные вопросы.
7. Содержание отчета:
7.1. Титульный лист.
7.2. Цель работы.
7.3. Результаты и ход выполнения работы.
7.4. Выводы, ответы.
8. Контрольные вопросы:
8.1. Понятие первообразной.
8.2. Понятие неопределенного интеграла.
8.3. Свойства неопределенного интеграла.
8.4. Формула интегрирования заменой переменной.
8.5. Формула интегрирования по частям.
9. Приложение:
9.1. Задания:
Вариант 1
1. 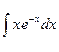 ; 3.
; 3. 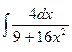 ; 5.
; 5. 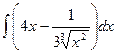 .
.
2. 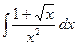 ; 4.
; 4. 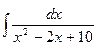 ;
;
Вариант 2
1. 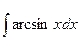 ; 3.
; 3. 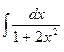 ; 5.
; 5. 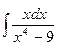 .
.
2. 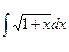 ; 4.
; 4. 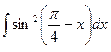 ;
;
Вариант 3
1. 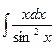 ; 3.
; 3. 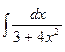 ; 5.
; 5. 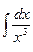 .
.
2. 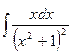 ; 4.
; 4. 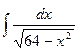 ;
;
Вариант 4
1. 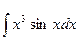 ; 3.
; 3. 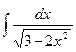 ; 5.
; 5. 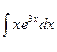 .
.
2. 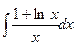 ; 4.
; 4. 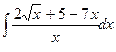 ;
;
Вариант 5
1. 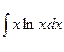 ; 3.
; 3. 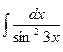 ; 5.
; 5. 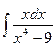 .
.
2. 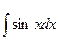 ; 4.
; 4. 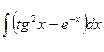 ;
;
Вариант 6
1. 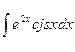 ; 3.
; 3. 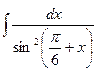 ; 5.
; 5. 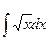 .
.
2. 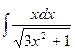 ; 4.
; 4. 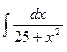 ;
;
Вариант 7
1. 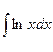 ; 3.
; 3. 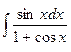 ; 5.
; 5. 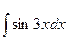 .
.
2. 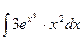 ; 4.
; 4. 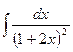 ;
;
Вариант 8
1. 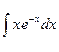 ; 3.
; 3. 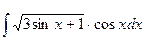 ; 5.
; 5. 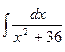 .
.
2. 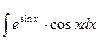 ; 4.
; 4. 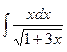 ;
;
Методические указания.
Отыскание функции F(x) по известному дифференциалу dF(x)=f(x)dx (или по известной ее производной F'(x)=f(x)) т.е. действие обратное дифференцированию, называются интегрированием, а искомая функция F(x) называется первообразной функцией от функции f(x).
Совокупность всех первообразных F(x)+C от функции f(x) называется неопределенным интегралом от этой функции:
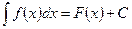
Основные формулы интегрирования.
1. 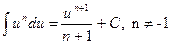
2. 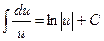
3. 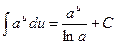
4. 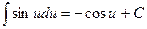
5. 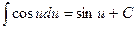
6. 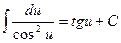
7. 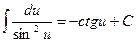
8. 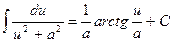
9. 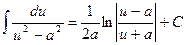
10. 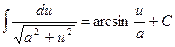
Методы интегрирования.
- Непосредственное интегрирование.
Найти интеграл: 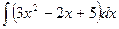
Решение: Интегрируя каждое слагаемое отдельно, получим:
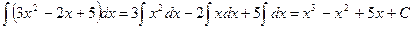
- Интегрирование посредствам замены переменной.
Для нахождения интеграла 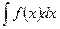 можно заменить переменную x новой переменной t, связанной с x подходящей функцией
можно заменить переменную x новой переменной t, связанной с x подходящей функцией 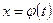 . Определив из этой формулы
. Определив из этой формулы 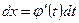 и подставляя, получим
и подставляя, получим
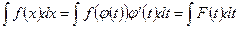
Если интеграл с новой переменной интегрирования t будет найден, то преобразовав результат к переменной x, пользуясь исходной функцией 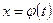 , получим искомое выражение заданного интеграла.
, получим искомое выражение заданного интеграла.
Найти интеграл: 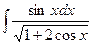 .
.
Решение: Положим t=1+2cosx. Тогда td=-2sinxdx.
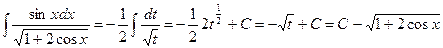
- Интегрирование по частям.
Из формулы дифференциала произведения d(uv)=udv+vdu интегрированием обеих частей равенства получается формула интегрирования по частям:
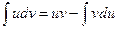 .
.
Найти интеграл 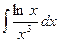 .
.
Решение. Пусть u=lnx, 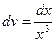 . Тогда
. Тогда 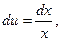
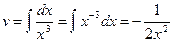
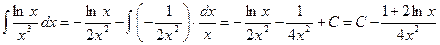
Интегрируя обе части равенства d(uv) = udv+vdu, получим
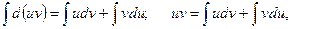
откуда
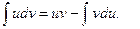
С помощью этой формулы вычисление интеграла 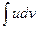 сводится к вычислению интеграла
сводится к вычислению интеграла 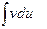 ,если последний окажется проще исходного.
,если последний окажется проще исходного.
Пример.1 Найти следующий интеграл:
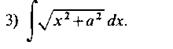
Решение. Положим 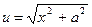 , dv=dx; тогда
, dv=dx; тогда 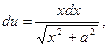 v=x. По формуле получим
v=x. По формуле получим
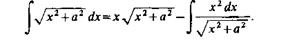
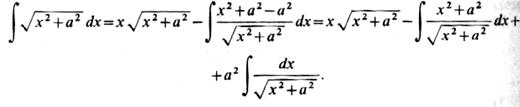 |
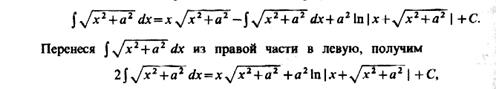 |
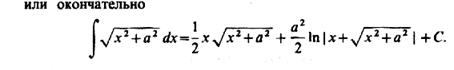 |
В числителе подынтегральной функции последнего интеграла прибавим и представим этот интеграл в виде суммы двух интегралов:
