ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Наименование работы: ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ, ЕГО ПРИМЕНЕНИЕ ДЛЯ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск
2012 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (2 курс)
Наименование работы: ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ, ЕГО ПРИМЕНЕНИЕ ДЛЯ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ.
1. Цель работы:Приобретение навыков нахождения частных производных функций двух переменных, вычисления полного дифференциала функции двух переменных, применять дифференциал функции для приближенных вычислений.
2. Литература:
2.1. В.А. Подольский, А.М. Суходольский "Сборник задач по математике" гл.14 §1-3 М.: Высшая школа, 1978 г.
3. Подготовка к работе:
3.1. Изучить теоретический материал по теме “Полный дифференциал функции двух переменных ”.
3.2. Подготовить бланки отчета.
3.3. Подготовить ответы на вопросы допуска к работе:
3.3.1. Понятие функции нескольких переменных.
3.3.2. Понятие частой производной функции двух переменных.
3.3.3. Понятие полного дифференциала функции двух переменных, формула вычисления полного дифференциала.
3.3.4. Формула применения полного дифференциала для вычисления приближенного значения функции двух переменных в точке.
4. Основное оборудование:
4.1. Литература, конспект.
5. Задание:
5.1. Вычислить полный дифференциал функции двух переменных в точке.
5.2. Вычислить приближенное значение функции с использованием дифференциала.
6. Порядок выполнения работы:
6.1. Записать задание своего варианта в отчет.
6.2. Вычислить полный дифференциал функции двух переменных в точке.
6.3. Вычислить приближенное значение функции с использованием дифференциала.
6.4. Записать ответы, оформить отчет.
6.5. Подготовить ответы на контрольные вопросы.
7. Содержание отчета:
7.1. Титульный лист.
7.2. Цель работы.
7.3. Результаты и ход выполнения работы.
7.4. Выводы, ответы.
8. Контрольные вопросы:
8.1. Понятие функции нескольких переменных.
8.2. Понятие частой производной функции двух переменных.
8.3. Понятие полного дифференциала функции двух переменных, формула вычисления полного дифференциала.
8.4. Формула применения полного дифференциала для вычисления приближенного значения функции двух переменных в точке.
9. Приложение:
| Вариант 1. | Вариант 2. |
1) 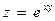 в точке (-2,03; -0,8) 2) в точке (-2,03; -0,8) 2) 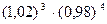 | 1) 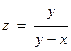 в точке (1,5; 1,97) 2) в точке (1,5; 1,97) 2) 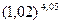 |
| Вариант 3. | Вариант 4. |
1) 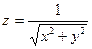 в точке (2,9; 3,04) 2) в точке (2,9; 3,04) 2) 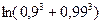 | 1) 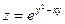 в точке (1,01; 2,01) 2) в точке (1,01; 2,01) 2) 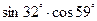 |
| Вариант 5. | Вариант 6. |
1) 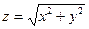 в точке (2,06; 3,04) 2) в точке (2,06; 3,04) 2) 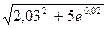 | 1) 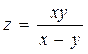 в точке (1,5; 1,97) 2) в точке (1,5; 1,97) 2) 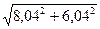 |
| Вариант 7. | Вариант 8. |
1) 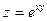 в точке (2,07; 3,06) 2) в точке (2,07; 3,06) 2) 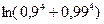 | 1) 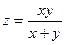 в точке (2,01; 1,01) 2) в точке (2,01; 1,01) 2) 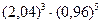 |
10. Методические указания.
Пусть функция y = f(x) имеет производную в точке х:
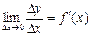
Тогда можно записать: 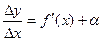 , где a®0, при Dх®0.
, где a®0, при Dх®0.
Следовательно: 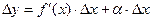 .
.
Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.
Определение. Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции.
 Обозначается dy или df(x).
Обозначается dy или df(x).
Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx.
Можно также записать: