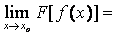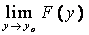Определение предела функции
Определение 4.1. Пусть функция f(х) определена на некотором интервале (а,в). Число А называется пределом функции f(х) в точке хо, т.е.
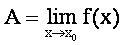 ,
,
если " e > 0 $ d = d(e) > 0: "х Î ( а, в), удовлетворяющих условию
çх - хоç < d, х ¹ хо 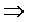 (4.1)
(4.1)
çf(x) - Aç < e. (4.2)
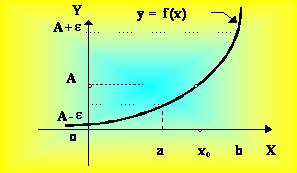 Рис. 4.1. Рис. 4.1. |
Таким образом, число А называется пределом функции f(х) в точке хо A = 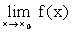 , при х ® хо тогда и только тогда, когда для любого (") e > 0 существует ( $) такая дельта окрестность d = d (e) > 0 точки хо :
, при х ® хо тогда и только тогда, когда для любого (") e > 0 существует ( $) такая дельта окрестность d = d (e) > 0 точки хо :
"х Î (а, в) : х Î O ( хо , d), х ¹хо Þ f ( x ) Î O ( A, e ).
Замечание.
Понятие предела, естественно, переносится на функции нескольких переменных.
Пусть f (х, у) - функция двух переменных, заданная на множество Х плоскости Оху.
Под окрестностью Оа,в точки Мо (а, в) (а и в - конечные) будем понимать внутренность любого прямоугольника {a1 < х < b1 , a2 < у < b2 }, построенного вокруг точки Мо (т.е. a1 < а < b1 , a2 < в < b2 ), из которого удалена сама точка Мо.
В таком утверждении можно записать 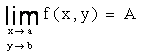
" e > o $ Oа,в : " M (х ,у ) Î Oа,в Þ ç f (x, y) - A ç < e.
При этом предполагается, что в любой Оа,в $ M (х,у ), в которых f (х, у) имеет смысл (предельная точка).
Односторонние пределы функции
Введем понятие левой и правой окрестности точки хо - число.
Определение 4.2. Любой интервал 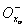 = (a, xo) ((
= (a, xo) (( 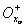 = (xо, b )), правым (левым) концом которого является точка хо, назовем ее левой (правой) окрестностью.
= (xо, b )), правым (левым) концом которого является точка хо, назовем ее левой (правой) окрестностью.
Символически факт, что х принимает лишь значения, принадлежащие некоторой левой окрестности точки хо, будем обозначать
х ® хо - 0, х < хо.
Аналогично х ® хо + 0 , х > хо .
Определение 4.3. Число А называется пределом функции слева, если
çf( x) - A ç < e.
И будем писать 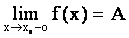 , где Х - область определения f (х).
, где Х - область определения f (х).
Аналогично 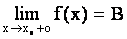 - предел функции справа.
- предел функции справа.
Замечание.
Можно, конечно, ограничиться рассмотрением левых d - окрестностей точки хо : 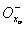 = (хо - d, хо ) , где d = d ( e ) > 0.
= (хо - d, хо ) , где d = d ( e ) > 0.
 = (xo , xo + d), где d = d ( e ) > 0.
= (xo , xo + d), где d = d ( e ) > 0.
O(xо - 0, d ) = { х: хо - d < x £ хо }, d > 0
O(х + 0, d ) = {х : хо £ х < xo + d }, d > 0.
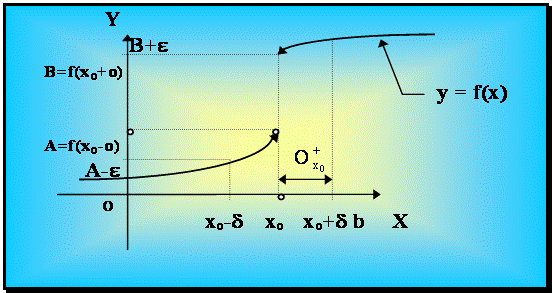
Рис. 4.2.
Пример 4.1.
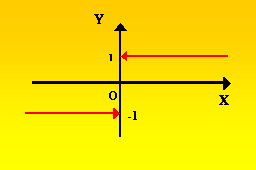 Рис. 4.3. Рис. 4.3. |
Пусть f(х) = sin х = 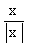 ,определена для всех x ¹ 0.
,определена для всех x ¹ 0.
Здесь 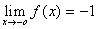 , а
, а 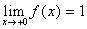 .
.
Теорема 4.1. Для существования предела функции f(х) при х ® хо (хо - число) Û f(хо - о) = f(хо + о).
Доказательство: Пусть  ,
,
тогда " e > о $ d = d(e) > о: çх -хоç< d = > çf (х) ¹ A ç < e,
и следовательно $ 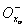 = (хо - d, хо) и
= (хо - d, хо) и 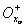 = ( xо , xо + d ) :
= ( xо , xо + d ) :
А =  и А =
и А =  .
.
Обратно, если существуют пределы А = 
 f(x) и А =
f(x) и А =  , то " e > 0 $ d1 = d1 (e) и d2 = d2 (e) такие, что, если
, то " e > 0 $ d1 = d1 (e) и d2 = d2 (e) такие, что, если
хо - d1 < х < хо и, соответственно, хо < х < xо + d2 Þ
çf(х) - Aç < e
Возьмем d = min {d1, d2} Þ çf( x ) - A ½< e при çх -хоç< d,
х ¹ хо. И тогда, согласно определения 3.1 
 .
.
Лемма 4.1. Если f(х) имеет предел в точке хо, то существует окрестность этой точки (быть может, выброшенной точкой хо), на которой функция ограничена.
Теорема 4.2. (Правило замены переменного для пределов функции)
Пусть существуют 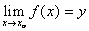 o, f(х) ¹ уо " х ¹ хо и
o, f(х) ¹ уо " х ¹ хо и  Þ при х ® хо существует предел сложной функции F[f(x)] и
Þ при х ® хо существует предел сложной функции F[f(x)] и