Основная идея и особенности вычислительного метода динамического программирования
Глава 7. Динамическое программирование
1. Основная идея и особенности вычислительного метода динамического программирования
2. Задачи управления запасами
3. Динамические задачи управления запасами
ОСНОВНАЯ ИДЕЯ И ОСОБЕННОСТИ ВЫЧИСЛИТЕЛЬНОГО МЕТОДА ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Динамическое программирование - это вычислительный метод для решения задач оптимизаци специальной структуры с адитивними или мультипликативными целевыми функциями.
Динамическое программирование возникло и сформировалось в 1950-1953 гг. благодаря работам Р. Беллмана и его сотрудников. Первые задачи, которые привели к появлению вычислительного метода, были динамическими задачами управления запасами.
Идею вычислительного метода динамического программирования (ДП) рассмотрим на следующем примере:
максимизировать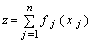 
(7.1.1)
при условиях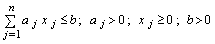 
(7.1.2 )
Как видно, целевая функция задачи и ограничение являются суммой функций от одной переменной каждая. Такая функция, как известно, называется адитивной. Если все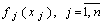 
выпуклые, то для решения задачи можно применить метод множителей Лагранжа.
Если имеется много локальных минимумов, то этот метод дает лишь один из них. Если надо найти глобальный максимум, метод множителей Лагранжа применить невозможно.
Поэтому рассмотрим другой метод, обеспечивающий отыскание глобально-оптимального решения. Предположим, что все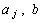 
- целые числа. Предположим также, что в рассматриваемой задаче все переменные могут принимать лишь целочисленные значения.
Через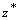 
обозначим абсолютный (глобальный) максимум 
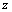при условии 
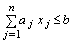. Выберем некоторое значение 
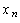и, зафиксировав его, максимизируем 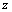по всем остальным переменным 
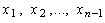. Предположим, что такая максимизация проведена для всех возможных значений 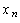. Тогда 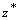будет наибольшим из всех возможных значений 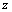. Формально этот процесс (эта процедура) записывается так:
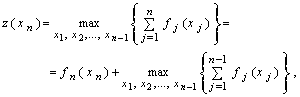(7.1.3)
причем
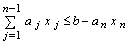. (7.1.4)
Поскольку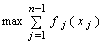 
для неотрицательных целых чисел, удовлетворяющих условию (7.1.4), зависит от 
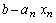, то обозначим
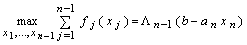. (7.1.5)
Предположим, что мы вычислили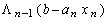 
для всех допустимых целых значений = 
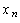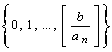, где 
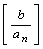означает целую часть 
.
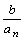Очевидно, что
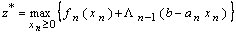. (7.1.6)
Для вычисления (7.1.6) определим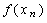 
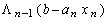и для всех допустимых значений 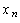и выберем максимальное 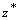. Одновременно найдем оптимальное решение 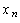. Таким образом, если бы была известна функция 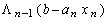, то вся задача свелась бы к задаче с одной переменной.
Покажем, как вычислить .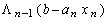
Обозначим
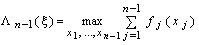
при условии
.
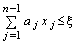Повторив вышеприведенные выкладки, получим
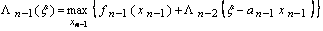, (7.1.7)
где
, (7.1.8)
причем максимум в (7.1.7) отыскивается при условии
.
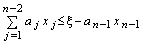Аналогичным образом вычисляем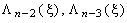 
и т.д. В конце концов на 
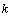-м шаге мы используем 'основное рекуррентное соотношение (ОРС) динамического программирования'
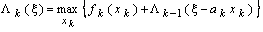(7.1.9)
при условии, что
.
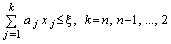Используя ОРС (7.1.9), организуем процесс вычислений, как многошаговый процесс, следующим образом. На первом шаге, зафиксировав начало интервала 0 и изменяя его правый конец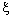 
, вычисляем
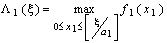(7.1.10)
для всех возможных значений 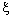=0, 1, . , b. Оптимальное решение первого шага обозначим через 
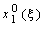. Составляем таблицу динамического программирования первого шага (табл. 7.1) и заполняем ее результатами вычислений.
На втором шаге ( 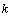=2) находим 
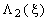в соответствии с соотношением
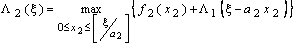, (7.1.11)
причем значения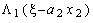 
берем из табл. 7.1.
Вычисляем последовательно 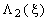для всех значений 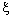= 0,1,., 
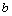, используя результаты табл. 7.1. Одновременно находим 
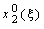и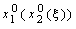 
. Результаты вычислений заносим в таблицу второго шага (табл. 7.2).
| Таблица 7.1 | Таблица 7.2 | ||||||
 |  |  | |  | | | |
 | |
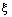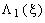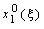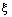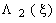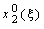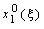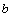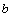Дале, пользуясь соотношением (7.1.8), последовательно вычисляем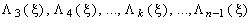 
для всех значений
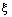= 0, 1, 2, ., .
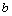В конце концов, на последнем шаге при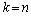 
находим
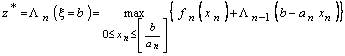, (7.1.12)
а также соответствующее оптимальное значение для последней переменной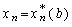 
. Для отыскания значений всех остальных переменных 
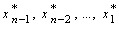надо воспользоваться таблицей 
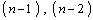и т.д. шагов. Полагая 
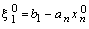, из таблицы предшествующего шага находим (без вычислений)
.
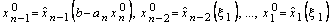Следовательно, динамическое программирование - это направленный последовательный перебор вариантов, который обязательно приводит к глобальному максимуму. Для применения метода необходимо табулировать функции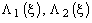 
, . , 
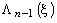для всех допустимых значений .
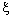Сравним метод динамического программирования по числу необходимых операций с простым перебором вариантов. Для упрощения расчетов примем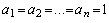 
.
При простом переборе число возможных вариантов (при условии целочисленности всех переменных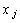 
) равно числу способов, которыми можно разместить 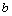одинаковых шаров в 
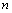урн. Оно составляет
.
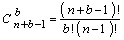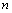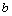Например, при = 5, = 20,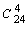 
= 10626.
Оценим число операций, требуемых для решения этой задачи методом динамического программирования.
Для вычисления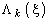 
при фиксированном 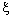необходимо выполнить ( 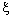+1) вычислений функции 
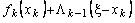при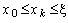 
. Следовательно, чтобы заполнить одну таблицу (при 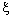=0,1, ., 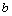) необходимо 
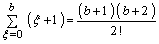операций.
Таким образом, для вычисления всех функций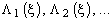 
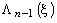, необходимо 
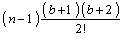операций.
С учетом вычислений функции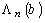 
общее число операций составляет
.
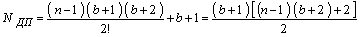Это значительно меньше, чем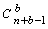 
, то есть имеем существенное сокращение объема вычислений сравнительно с простым перебором.
Подведем некоторые итоги. Рассмотренную выше задачу (7.1.1), (7.1.2) с экономической точки зрения можно трактовать как задачу распределения одного ограниченного ресурса 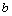между 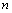разными способами производства, где 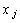- объем производства по 
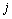-му способу ; 
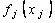- прибыль от достижения объема ; 
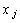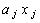- затраты ресурса на производство по 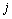-му способу (при ограничении на общий объем использованного ресурса 
).
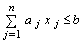Поэтому 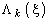можно трактовать как максимальную прибыль от первых 
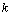способов производства, когда общий объем ресурса (сырья) равен 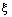единиц.
Рассматриваемую задачу можно интерпретировать как 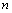-шаговый процесс принятия решений, где на 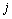-м шаге принимается решение о том, какое количество ресурса из общего объема 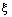следует выделить на переработку по 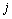-му способу производства. Как видим, структура этой задачи не изменяется от числа шагов, то есть задача инвариантна относительно .
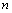Решение для 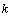-шаговой задачи получается из решения для ( 
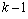)-шаговой задачи путем добавления 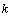-го шага и использования результатов предыдущего ( 
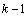)-го шага.
Следовательно, сущность динамического программирования состоит в замене решения данной 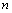-шаговой задачи последовательностью одношаговых задач.
Подводя итоги, назовем главные признаки (свойства) задач, к которым можно применить метод динамического программирования:
Задача должна допускать интерпретацию как 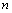-шаговый процесс принятия решений.
Задача должна быть определена для любого числа шагов и иметь структуру, не зависящую от их числа.
Для k-шаговой задачи должно быть задано некоторое множество параметров, описывающих состояние системы, от которых зависят оптимальные значения переменных. Это множество не должно изменяться при увеличении числа шагов. (В рассматриваемом выше примере таким параметром было общее количество ресурса.)
Выбор решения (стратегии управления) на 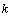-м шаге не должен влиять на предыдущие решения, кроме необходимого пересчета переменных.
Пусть 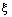- вектор параметров, описывающих состояние процесса (вектор состояния). Тогда оптимальное значение целевой функции для 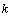-шагового процесса 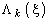будем называть функцией состояния.
Пусть Xk - вектор переменных управления (стратегия), который необходимо определить на 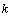-м шаге. Тогда для задач, к которым можно применить метод динамического программирования, должно выполняться следующее основное рекуррентное соотношение:
,
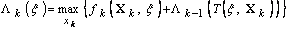где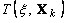 
- вектор состояния предыдущего ( 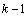)-го шага при условиях 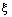и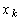 
. В рассматриваемой задаче 
.
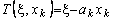Сформулируем принцип оптимальности Беллмана, который обосновывает это соотношения [4; 18].
Оптимальная стратегия обладает следующим свойством : для любых начального состояния и начальной стратегии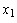 
, стратегия на 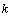-м шаге должна быть оптимальной только относительно текущего состояния системы и не должны зависеть от предыдущих состояний.
Таким образом, принцип оптимальности Беллмана утверждает, что оптимальное управление системой на каждом шаге не зависит от предыстории процесса, то есть как система достигла текущего состояния, а определяется только этим состоянием. Системы (процессы), которые имеют такое свойство, называются марковскими.