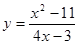Самостоятельная работа № 1
Глава 1. Введение в анализ. Дифференциальное исчисление функции одной переменной.
Теоретические вопросы
- Понятие функции одной переменной.
- Предел функции.
- Непрерывность функции.
- Бесконечно малые функции и их свойства.
- Бесконечно большие функции и их свойства.
- Односторонние пределы.
- Производная функции.
- Таблица производных.
- Правила дифференцирования.
- Производная сложной функции.
- Производные высших порядков. Правило Лопиталя.
- Исследование функций с помощью производных.
Литература
- Н.С. Пискунов Дифференциальное и интегральное исчисления для втузов.- М.:Наука,1989,т.1,2.
- В.С. Щипачев Высшая математика.- М.: Высшая школа, 1990.
- П.Е. Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах.- М.: Высшая школа,1998,ч.1,2.
- Предел функции
Пусть функция 
 определена на множестве
определена на множестве 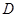 . Число А называется пределом функции
. Число А называется пределом функции 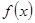 при
при 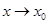 , если
, если 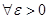
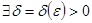 , что
, что 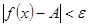 при
при 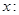
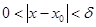 .
.
Это записывают так:
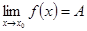 .
.
Если 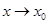 и
и 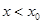 , то используют запись
, то используют запись 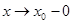 ; если
; если 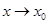 и
и 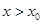 , то
, то 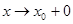 .
.
Числа 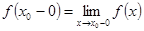 и
и 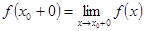 называются соответственно левосторонним и правосторонним пределами функции
называются соответственно левосторонним и правосторонним пределами функции 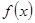 в точке
в точке 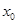 .
.
Если существуют пределы 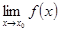 и
и 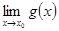 , то:
, то:
1) 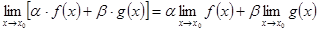 , где
, где 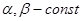 ;
;
2) 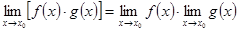 ;
;
3) 
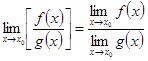
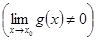 .
.
При решении задач полезно знать следующие “замечательные” пределы:
1) 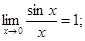 2)
2) 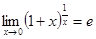 ; 3)
; 3) 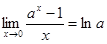 ; 4)
; 4) 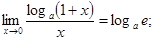
5) 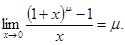
Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида 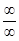 ,
, 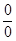 ,
, 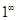 ,
, 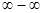 , и т.д.
, и т.д.
Существуют различные приемы раскрытия данных неопределенностей:
деление числителя и знаменателя на старшую степень переменной (при 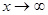 ); сокращение на множитель, создающий неопределенность; применение “замечательных” пределов и т.п.
); сокращение на множитель, создающий неопределенность; применение “замечательных” пределов и т.п.
Задание 1. Найти пределы функций, не пользуясь правилом Лопиталя.
1) 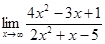
Решение. При 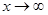 получаем неопределенность вида
получаем неопределенность вида 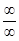 . Чтобы найти предел данной дробно - рациональной функции, необходимо предварительно разделить числитель и знаменатель дроби на
. Чтобы найти предел данной дробно - рациональной функции, необходимо предварительно разделить числитель и знаменатель дроби на 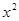 , т.к. степень
, т.к. степень 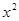 - наивысшая степень многочленов, определяющих данную рациональную функцию. Применяя основные теоремы о пределах и свойства бесконечно малых величин, получаем:
- наивысшая степень многочленов, определяющих данную рациональную функцию. Применяя основные теоремы о пределах и свойства бесконечно малых величин, получаем:
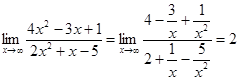
2) 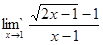
Решение. Непосредственная подстановка предельного значения аргумента 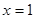 приводит к неопределенности вида
приводит к неопределенности вида 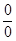 . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму 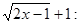
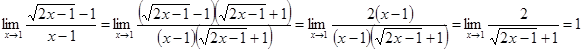
3) 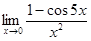
Решение Здесь имеет место неопределенность вида 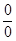 . Вычисление данного предела основано на применении первого “ замечательного” предела (
. Вычисление данного предела основано на применении первого “ замечательного” предела ( 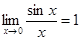 ).Имеем:
).Имеем: 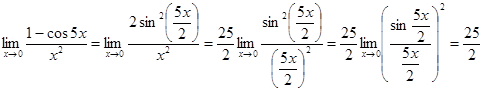
4) 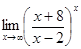
Решение. При 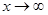 данная функция представляет собой степень, основание которой стремится к 1, а показатель – к
данная функция представляет собой степень, основание которой стремится к 1, а показатель – к 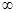 (неопределенность вида
(неопределенность вида 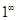 ). Преобразуем функцию так, чтобы использовать второй “замечательный” предел (
). Преобразуем функцию так, чтобы использовать второй “замечательный” предел ( 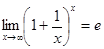 ). Получим:
). Получим:
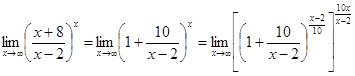 .
.
Так как 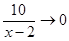 при
при 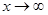 ,то
,то 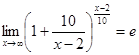 . Учитывая, что
. Учитывая, что 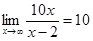 , находим
, находим 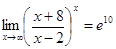 .
.
- Непрерывность функции
Функция 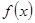 называется непрерывной в точке
называется непрерывной в точке 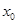 , если:
, если:
1) эта функция определена в некоторой окрестности точки 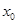
2) 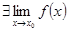
3) 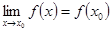 .
.
Теорема. Для того чтобы функция 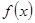 была непрерывна в точке
была непрерывна в точке 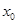 , необходимо и достаточно, чтобы выполнялись равенства:
, необходимо и достаточно, чтобы выполнялись равенства: 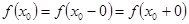 .
.
Точка 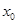 называется точкой разрыва непрерывности функции, если в этой точке функция не является непрерывной, т.е. если в этой точке нарушается хотя бы одно из условий определения непрерывности функции.
называется точкой разрыва непрерывности функции, если в этой точке функция не является непрерывной, т.е. если в этой точке нарушается хотя бы одно из условий определения непрерывности функции.
Если существуют конечные односторонние пределы 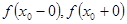 , причем не все три числа
, причем не все три числа 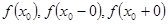 равны между собой, то
равны между собой, то 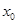 называется точкой разрыва первого рода. В частности, если:
называется точкой разрыва первого рода. В частности, если:
1) 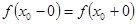 , то
, то 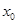 называется устранимой точкой разрыва;
называется устранимой точкой разрыва;
2) 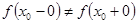 , то
, то 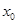 называется точкой разрыва типа скачка, причем разность
называется точкой разрыва типа скачка, причем разность 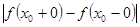 называется скачком функции
называется скачком функции 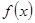 в точке
в точке 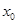 .
.
Точки разрыва функции, не являющиеся точками разрыва первого рода, называются точками разрыва второго рода.
Справедливо следующее утверждение.
Задание 2. Задана функция 
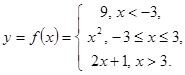
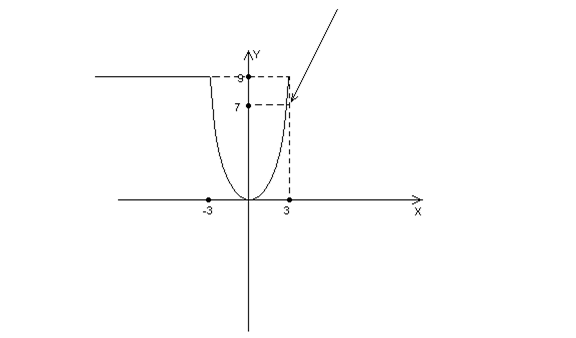
Исследовать функцию на непрерывность. Сделать чертеж.
Решение Функция 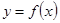 задана различными непрерывными аналитическими выражениями для различных областей изменения аргумента
задана различными непрерывными аналитическими выражениями для различных областей изменения аргумента 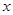 . Следовательно, точками разрыва данной функции могут быть только те точки, в которых меняются аналитические выражения функции, т.е. точки
. Следовательно, точками разрыва данной функции могут быть только те точки, в которых меняются аналитические выражения функции, т.е. точки 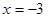 и
и 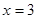 . Определим значения функции и ее односторонние пределы в этих точках:
. Определим значения функции и ее односторонние пределы в этих точках:
1) 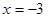 :
:
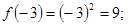
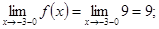
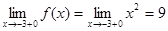 .
.
Так как 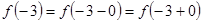 , то в точке
, то в точке 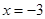 функция
функция 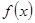 непрерывна.
непрерывна.
2) 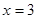 :
:
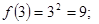
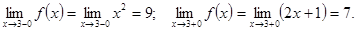
Так как 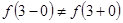 , то точка
, то точка 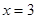 является точкой разрыва непрерывности функции
является точкой разрыва непрерывности функции 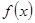 первого рода типа скачка.
первого рода типа скачка.
Скачок функции в точке разрыва равен: 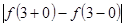 =2. График функции
=2. График функции 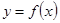 представлен на рисунке:
представлен на рисунке:
- Дифференцирование функций
Производной 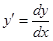 функции
функции 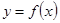 в точке
в точке 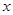 называется предел отношения приращения функции
называется предел отношения приращения функции 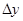 к приращению аргумента
к приращению аргумента 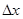 , при условии, что
, при условии, что 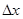 стремится к нулю.
стремится к нулю.
То есть:
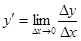 .
.
Основные правила нахождения производной
Если 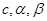 -
- 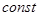 и
и 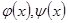 - дифференцируемые функции в точке
- дифференцируемые функции в точке 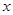 , (т.е. функции, имеющие производные в точке
, (т.е. функции, имеющие производные в точке 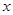 ), то:
), то:
1) 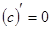 ;
;
2) 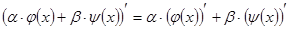 ;
;
3) 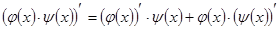
4) 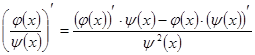 .
.
Таблица производных основных функций
1. 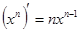 8.
8. 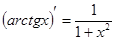
2. 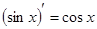 9.
9. 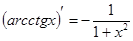
3. 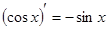 10.
10. 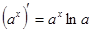
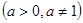
4. 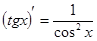 11.
11. 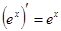
5. 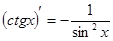 12.
12. 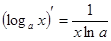
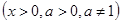
6. 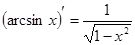

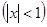 13.
13. 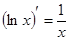
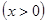
7. 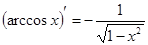

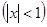
Правило дифференцирования сложной функции. Если 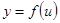 и
и 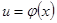 , т.е.
, т.е. 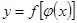 , где
, где 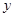 и
и 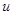 имеют производные, то
имеют производные, то
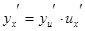 .
.
Дифференцирование функции, заданной параметрически. Пусть зависимость переменной 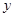 от переменной
от переменной 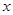 задана параметрически посредством параметра
задана параметрически посредством параметра 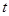 :
:
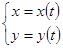 ,
,
Тогда
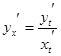 .
.
Задание 3. Найти производные данных функций.
1) 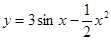
Решение. Применяя правило 2 нахождения производных и формулы 1 и 2 таблицы производных, получаем:
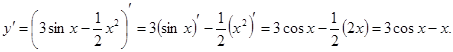
2) 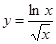
Решение. Применяя правило 4 нахождения производных и формулы 1 и 13 таблицы производных, получаем:
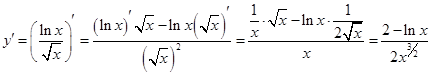 .
.
3) 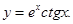
Решение. Применяя правило 3 нахождения производных и формулы 5 и 11 таблицы производных, получаем:
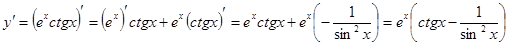 .
.
4) 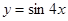
Решение. Полагая 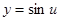 , где
, где 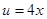 , согласно формуле нахождения производной сложной функции, получим:
, согласно формуле нахождения производной сложной функции, получим:
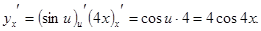
5) 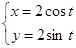
Решение. Имеем: 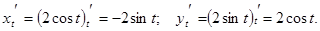 Тогда, согласно формуле нахождения производной функции, заданной параметрически, получаем:
Тогда, согласно формуле нахождения производной функции, заданной параметрически, получаем:
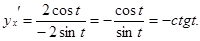
- Производные высших порядков. Правило Лопиталя.
Производной второго порядка функции 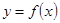 называется производная от ее производной, т.е.
называется производная от ее производной, т.е. 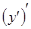 . Для второй производной используются следующие обозначения:
. Для второй производной используются следующие обозначения: 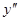 или
или 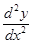 , или
, или 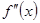 .
.
Производной 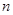 - го порядка от функции
- го порядка от функции 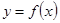 называется производная от ее производной
называется производная от ее производной 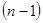 -го порядка. Для производной
-го порядка. Для производной 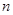 -го порядка используются следующие обозначения:
-го порядка используются следующие обозначения: 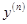 или
или 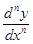 , или
, или 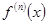 .
.
Правило Лопиталя. Пусть функции 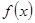 и
и 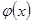 дифференцируемы в окрестности точки
дифференцируемы в окрестности точки 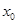 , причем производная
, причем производная 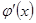 не обращается в нуль. Если функции
не обращается в нуль. Если функции 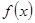 и
и 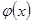 являются одновременно либо бесконечно малыми, либо бесконечно большими при
являются одновременно либо бесконечно малыми, либо бесконечно большими при 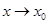 , и при этом существует предел отношения
, и при этом существует предел отношения 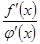 при
при 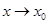 , то существует также и предел отношения
, то существует также и предел отношения 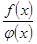 при
при 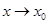 . Причем
. Причем
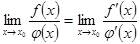 .
.
Правило применимо и в случае, когда 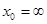 .
.
Заметим, что в некоторых случаях раскрытие неопределенностей вида 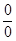 или
или 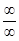 может потребовать неоднократного применения правила Лопиталя.
может потребовать неоднократного применения правила Лопиталя.
Неопределенности вида 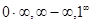 и т.д. с помощью элементарных преобразований легко сводятся к неопределенностям вида
и т.д. с помощью элементарных преобразований легко сводятся к неопределенностям вида 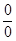 или
или 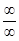 .
.
Задание 4. Найти предел 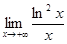 , пользуясь правилом Лопиталя.
, пользуясь правилом Лопиталя.
Решение Здесь мы имеем неопределенность вида 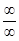 , т.к.
, т.к. 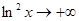 при
при 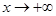 . Применим правило Лопиталя:
. Применим правило Лопиталя:
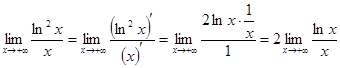 .
.
После применения правила Лопиталя мы снова получили неопределенность вида 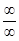
 , т.к.
, т.к. 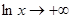 при
при 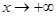 . Применяя снова правило Лопиталя повторно, получим:
. Применяя снова правило Лопиталя повторно, получим:
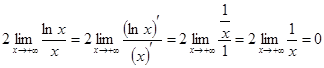 .
.
- Исследование функций
а) Возрастание и убывание функций
Функция 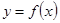 называется возрастающей на отрезке
называется возрастающей на отрезке 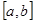 , если для любых точек
, если для любых точек 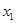 и
и 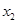 из отрезка
из отрезка 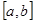 , где
, где 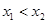 , имеет место неравенство
, имеет место неравенство 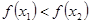 . Если функция
. Если функция 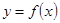 непрерывна на отрезке
непрерывна на отрезке 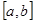 и
и 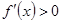 при
при 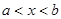 , то
, то 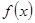 возрастает на отрезке
возрастает на отрезке 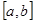 .
.
Функция 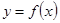 называется убывающей на отрезке
называется убывающей на отрезке 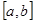 ,если для любых точек
,если для любых точек 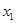 и
и 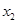 из отрезка
из отрезка 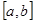 , где
, где 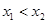 , имеет место неравенство
, имеет место неравенство 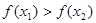 . Если функция
. Если функция 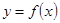 непрерывна на отрезке
непрерывна на отрезке 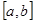 и
и 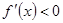 при
при 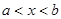 , то
, то 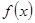 убывает на отрезке
убывает на отрезке 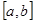 .
.
Если функция 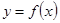 является только возрастающей или только убывающей на данном интервале, то она называется монотонной на интервале.
является только возрастающей или только убывающей на данном интервале, то она называется монотонной на интервале.
b) Экстремумы функций
Если существует 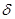 -окрестность точки
-окрестность точки 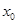
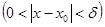 такая, что для всех точек
такая, что для всех точек 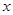 из этой окрестности имеет место неравенство
из этой окрестности имеет место неравенство 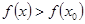 , то точка
, то точка 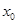 называется точкой минимума функции
называется точкой минимума функции 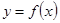 .
.
Если существует 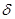 -окрестность точки
-окрестность точки 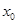
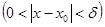 такая, что для всех точек
такая, что для всех точек 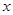 из этой окрестности имеет место неравенство
из этой окрестности имеет место неравенство 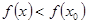 , то точка
, то точка 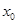 называется точкой максимума функции
называется точкой максимума функции 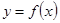 .
.
Точки максимума и минимума функции называются ее точками экстремума.
Точка 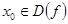 называется стационарной точкой, если
называется стационарной точкой, если 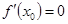 или
или 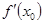 не существует.
не существует.
Если существует 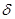 -окрестность стационарной точки
-окрестность стационарной точки 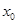 такая, что
такая, что 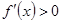 при
при 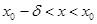 и
и 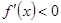 при
при 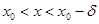 , то
, то 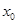 - точка максимума функции
- точка максимума функции 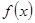 .
.
Если существует 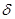 -окрестность стационарной точки
-окрестность стационарной точки 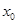 такая, что
такая, что 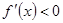 при
при 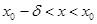 и
и 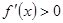 при
при 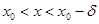 , то
, то 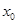 -точка минимума функции
-точка минимума функции 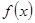 .
.
a) Направление выпуклости. Точки перегиба
График дифференцируемой функции 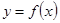 называется выпуклым вверх на интервале
называется выпуклым вверх на интервале 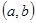 , еслион расположен ниже касательной, построенной к графику функции в любой точке этого интервала.
, еслион расположен ниже касательной, построенной к графику функции в любой точке этого интервала.
Достаточным условием выпуклости вверх графика функции 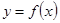 на интервале
на интервале 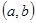 является выполнение неравенства
является выполнение неравенства 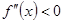 для любого
для любого 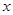 из рассматриваемого интервала.
из рассматриваемого интервала.
График дифференцируемой функции 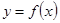 называется выпуклым вниз на интервале
называется выпуклым вниз на интервале 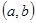 , еслион расположен выше касательной, построенной к графику функции в любой точке этого интервала.
, еслион расположен выше касательной, построенной к графику функции в любой точке этого интервала.
Достаточным условием выпуклости вниз графика функции 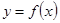 на интервале
на интервале 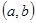 является выполнение неравенства
является выполнение неравенства 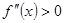 для любого
для любого 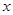 из рассматриваемого интервала.
из рассматриваемого интервала.
Точка 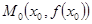 , в которой меняется направление выпуклости графика функции
, в которой меняется направление выпуклости графика функции 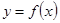 , называется точкой перегиба.
, называется точкой перегиба.
Точка 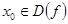 , где
, где 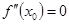 или
или 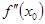 не существует, является абсциссой точки перегиба, если слева и справа от нее
не существует, является абсциссой точки перегиба, если слева и справа от нее 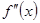 имеет разные знаки.
имеет разные знаки.
d) Асимптоты
Если расстояние от точки 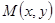 графика функции
графика функции 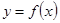 до некоторой прямой
до некоторой прямой 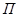 стремится к нулю при бесконечном удалении точки
стремится к нулю при бесконечном удалении точки 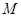 от начала координат, то прямую
от начала координат, то прямую 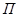 называют асимптотой графика функции.
называют асимптотой графика функции.
Если существует число 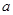 такое, что
такое, что 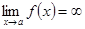 , то прямая
, то прямая 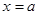 является вертикальной асимптотой.
является вертикальной асимптотой.
Если существуют пределы 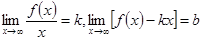 , то прямая
, то прямая 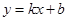 является наклонной (горизонтальной при k=0) асимптотой.
является наклонной (горизонтальной при k=0) асимптотой.
e) Общее исследование функции
Общее исследование функции рекомендуется проводить по следующей схеме:
1. Область определения функции
2. Точки пересечения графика с осями координат
3. Исследование функции на непрерывность, четность / нечетность и периодичность
4. Интервалы монотонности функции
5. Точки экстремума функции
6. Интервалы выпуклости и точки перегиба графика функции
7. Асимптоты графика функции
8. График функции.
Задание 5. Исследовать функцию 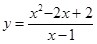 и построить ее график.
и построить ее график.
Решение. 1) Функция определена на всей числовой оси за исключением точки 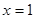 , где знаменатель дроби обращается в нуль.
, где знаменатель дроби обращается в нуль.
2) График данной функции пересекает координатную ось 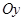 в точке
в точке 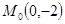 , т.к.
, т.к. 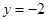 при
при 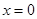 .
.
Чтобы найти точки пересечения графика функции с осью 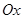 , необходимо решить уравнение
, необходимо решить уравнение 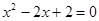 . Но данное уравнение не имеет действительных корней. Следовательно, у графика данной функции нет точек пересечения с осью
. Но данное уравнение не имеет действительных корней. Следовательно, у графика данной функции нет точек пересечения с осью 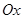 .
.
3) Данная функция непрерывна во всей области своего определения. Для исследования функции на четность проверим выполнение условия 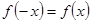 ; для исследования функции на нечетность проверим выполнение условия
; для исследования функции на нечетность проверим выполнение условия 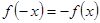 . Имеем:
. Имеем:
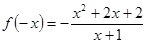 .
.
Так как 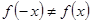 и
и 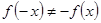 , то, следовательно, данная функция не обладает ни свойством четности, ни свойством нечетности.
, то, следовательно, данная функция не обладает ни свойством четности, ни свойством нечетности.
Исходная функция не периодична, т.к. 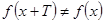 для любого
для любого 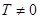 .
.
4) Найдем производную данной функции:

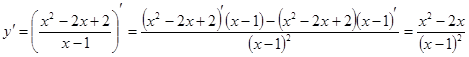 .
.
Определим стационарные точки. Для этого приравняем 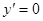 . Получим:
. Получим:
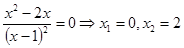 .
.
Производная 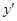 не существует в точке
не существует в точке 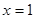 . Но точка
. Но точка 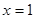 не принадлежит области определения данной функции. Следовательно, стационарными точками данной функции являются точки
не принадлежит области определения данной функции. Следовательно, стационарными точками данной функции являются точки 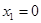 и
и 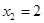 . Отметим все три точки на числовой оси:
. Отметим все три точки на числовой оси:
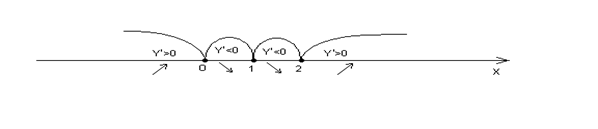
Определим знак производной на каждом интервале. Для этого достаточно подставить в производную любое значение 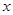 из рассматриваемого интервала. Результаты указаны на рисунке. Следовательно, исходная функция убывает на интервале
из рассматриваемого интервала. Результаты указаны на рисунке. Следовательно, исходная функция убывает на интервале 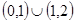 , возрастает на интервале
, возрастает на интервале 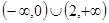 (что показано на рисунке).
(что показано на рисунке).
5) Так как производная меняет знак при переходе через стационарные точки, то эти точки являются точками экстремума. А именно, 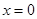 - точка максимума,
- точка максимума, 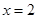 - точка минимума. Максимальное значение функции равно
- точка минимума. Максимальное значение функции равно 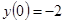 , минимальное значение
, минимальное значение 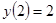 .
.
6) Вычислим вторую производную данной функции:
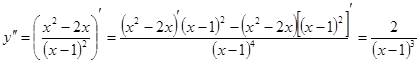 .
.
Вторая производная нигде не обращается в нуль, но 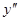 не существует при
не существует при 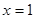 . Точка
. Точка 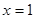 не принадлежит области определения данной функции. Отметим эту точку на числовой оси:
не принадлежит области определения данной функции. Отметим эту точку на числовой оси:

Определим знак второй производной на каждом интервале. Для этого достаточно подставить во вторую производную любое значение 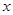 из рассматриваемого интервала. Результаты указаны на рисунке.
из рассматриваемого интервала. Результаты указаны на рисунке.
Следовательно, график данной функции является выпуклым вверх в интервале 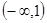 и выпуклым вниз в интервале
и выпуклым вниз в интервале 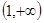 (что показано на рисунке).
(что показано на рисунке).
Так как вторая производная нигде не обращается в нуль и точка 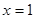 , где
, где 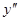 не существует, не принадлежит области определения данной функции, то у исходной функции нет точек перегиба.
не существует, не принадлежит области определения данной функции, то у исходной функции нет точек перегиба.
7) Найдем предел данной функции при 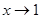 слева и справа:
слева и справа:
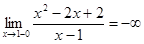 ,
, 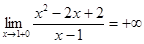 .
.
Следовательно, прямая 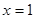 является вертикальной асимптотой.
является вертикальной асимптотой.
Для нахождения наклонной асимптоты вычислим следующие пределы:
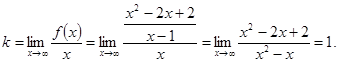
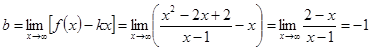 .
.
Следовательно, наклонная асимптота графика данной функции имеет вид 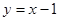 .
.
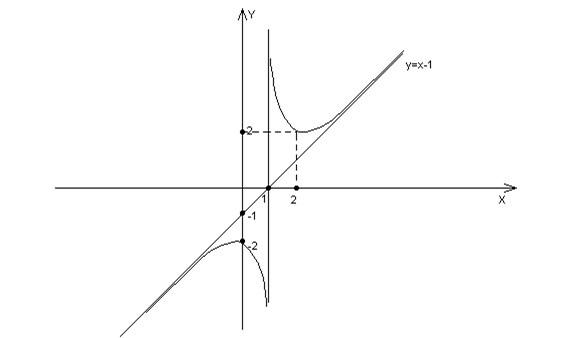
8) Используя полученные данные, построим график исходной функции:
Самостоятельная работа № 1
Введение в анализ. Дифференциальное исчисление функции одной переменной
Задание 1. Найти пределы функций, не пользуясь правилом Лопиталя.
1. а) 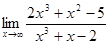 ; б)
; б) 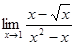 ; в)
; в) 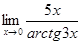 ; г)
; г) 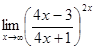
2. а) 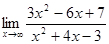 ; б)
; б) 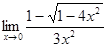 ; в)
; в) 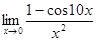 ; г)
; г) 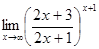
3. а) 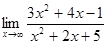 ; б)
; б) 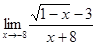 ; в)
; в) 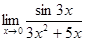 ; г)
; г) 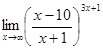
4. а) 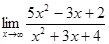 ; б)
; б) 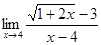 ; в)
; в) 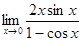 ; г)
; г) 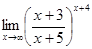
5. а) 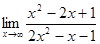 ; б)
; б) 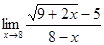 ; в)
; в) 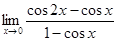 ; г)
; г) 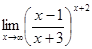
6. а) 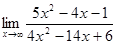 ; б)
; б) 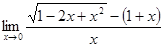 ; в)
; в) 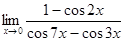 ;
;
г) 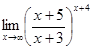
7. а) 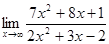 ; б)
; б) 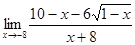 ; в)
; в) 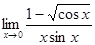 ; г)
; г) 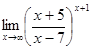
8. а) 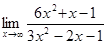 ; б)
; б) 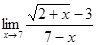 ; в)
; в) 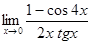 ; г)
; г) 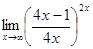
9. а) 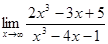 ; б)
; б) 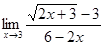 ; в)
; в) 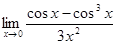 ; г)
; г) 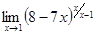
10. а) 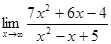 ; б)
; б) 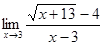 ; в)
; в) 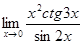 ; г)
; г) 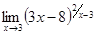 .
.
Задание 2. Исследовать на непрерывность данные функции. Сделать чертеж.
1. 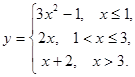 2.
2. 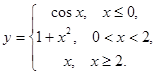
3. 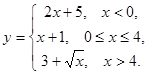 4.
4. 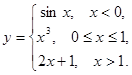
5. 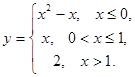 6.
6. 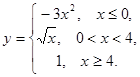
7. 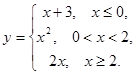 8.
8. 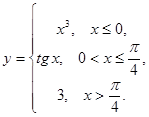
9. 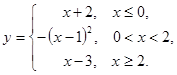 10.
10. 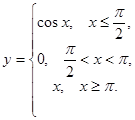
Задание 3. Найти производные данных функции.
- а)
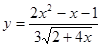 ; б)
; б) 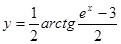 ; в)
; в) 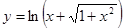 ;
;
г) 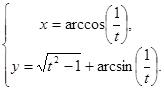
- a)
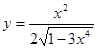 ; б)
; б) 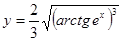 ; в)
; в) 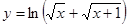 ;
;
г) 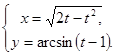
- a)
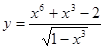 ; б)
; б) 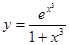 ; в)
; в) 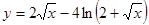 ; г)
; г) 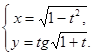
- а)
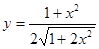 ; б)
; б) 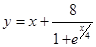 ; в)
; в) 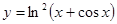 ; г)
; г) 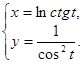
- а)
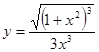 ; б)
; б) 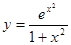 ; в)
; в) 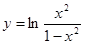 ; г)
; г) 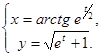
- а)
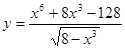 ; б)
; б) 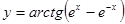 ; в)
; в) 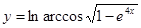 ;
;
г) 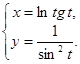
- а)
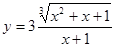 ; б)
; б) 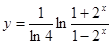 ; в)
; в) 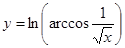 ; г)
; г) 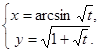
- а)
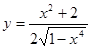 ; б)
; б) 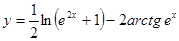 ; в)
; в) 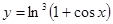 ;
;
г) 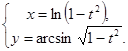
- а)
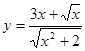 ; б)
; б) 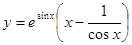 ; в)
; в) 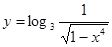 ; г)
; г) 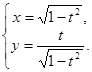
- а)
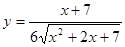 ; б)
; б) 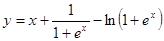 ; в)
; в) 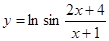 ;
;
г) 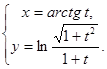
Задание 4. Найти пределы функций, пользуясь правилом Лопиталя.
1. 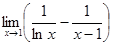 2.
2. 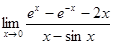
3. 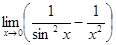 4.
4. 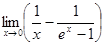 .
.
5. 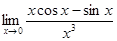 6.
6. 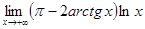
7. 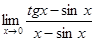 8.
8. 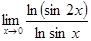
9. 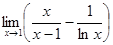 10.
10. 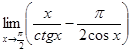
Задание 5. Провести полное исследование функций и построить их графики.
1. 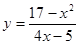 2.
2. 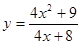
3. 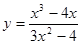 4.
4. 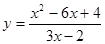
5. 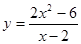 6.
6. 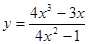
7. 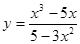 8.
8. 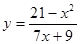
9. 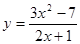 10.
10.