Определение деформаций и перемещений

Определим упругие деформации стержня предполагая, что изменение его длины при растяжении 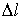, называемое абсолютной продольной деформацией или удлинением, мало по сравнению с его первоначальной длиной 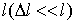. Тогда относительная продольная деформация будет равна

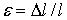
Учитывая, что согласно закону Гука для одноосного растяжения (сжатия)

,

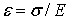где Е—;модуль продольной упругости материала стержня, а нормальные напряжения определяются по формуле — 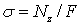(в нашем случае N_z=P), для абсолютной деформации получаем

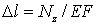(2)

Произведение EF принято называть жесткостью поперечного сечения стержня при растяжении (сжатии), так как удлинение обратно пропорционально EF.

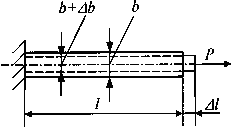
Рис.6. Модели продольной и поперечной деформаций

Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются (рис. 6), а при сжатии — увеличиваются. Это явление получило название эффекта Пуассона.

По аналогии с продольной деформацией изменение размеров поперечного сечения 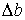(на рис. 6 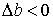) будем называть абсолютной поперечной деформацией, а 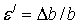— относительной поперечной деформацией. Относительные продольная и поперечная деформации, имеющие противоположные знаки, связаны между собой коэффициентом , являющимся константой материала и называемым коэффициентом поперечной деформации или коэффициентом Пуассона:

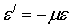
Как известно, для изотропного материала .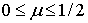

Формула (2) для удлинения стержня 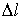применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EF=const, N_z =const). Удлинение стержня со ступенчатым изменением EF и N_z (рис. 7) может быть определено как сумма удлинений ступеней, у которых EF и N_z постоянны:

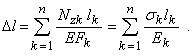
(индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов). В случае, когда N_z и EF меняются по длине стержня l непрерывно и их можно считать постоянными лишь в пределах ступеней длиной dz, обобщая формулу эту, получаем

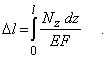
В качестве тестов для практики расчетов определенных интегралов рекомендую воспользоваться системой входных тестов Т-5, указанных в ПРИЛОЖЕНИИ.

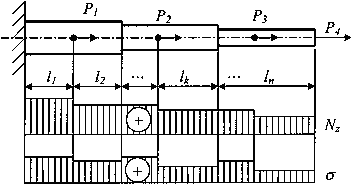
Рис.7. Ступенчатый брус

С упругими продольными деформациями стержня при растяжении (сжатии) связаны продольные перемещения его сечений. На рис. 8 приведены три случая определения таких перемещений, откуда видно, что перемещения поперечных сечений численно равны удлинениям заштрихованных частей стержня:

• перемещение свободного торцевого сечения 1—1 при неподвижном другом торцевом сечении (рис. 8, а) численно равно удлинению стержня;
• перемещение промежуточного сечения 2—2 (рис. 8, б) численно равно удлинению части стержня, заключенной между данным сечением и сечением неподвижным;
• взаимное перемещение сечений 3—3 и 4—4 (рис, 8, в) численно равно удлинению части стержня, заключенной между этими сечениями.

Рис.8. Модели перемещений

НАПРЯЖЕННОЕ СОСТОЯНИЕ ПРИ РАСТЯЖЕНИИ (СЖАТИИ)

Напряженное состояние при растяжении стержня является одноосным (рис. 9, а). Поскольку на поперечных и продольных площадках касательные напряжения не возникают, то эти площадки являются главными. Причем в случае растяжения 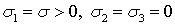, а в случае сжатия .

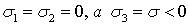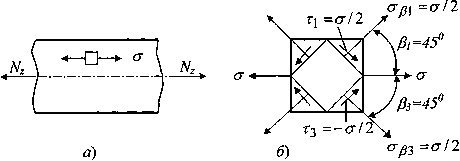
Рис.9. Напряженное состояние: а ) исходный элемент, б ) компоненты напряжений

Напряжения на площадках, наклоненных к оси стержня под углом , определяются по формулам для упрощенного плоского напряженного состояния:

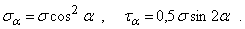
Площадки с экстремальными касательными напряжениями 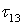(рис. 9, б), как известно, наклонены по отношению к исходным под углами 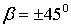(следует и из формулы для 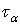) и равны .

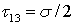Именно с действием экстремальных 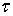связывается появление на боковой поверхности образца из малоуглеродистой стали, испытываемого на растяжение, линий скольжения, ориентированных под углом 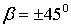к оси образца. На площадках с экстремальными 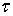действуют и нормальные напряжения, равные .

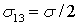Лекция № 13. Расчет статически неопределимых систем по допускаемым нагрузкам.