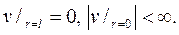Р е ш е н и е. Здесь нужно решать смешанную задачу

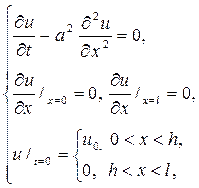
методом разделения переменных, полагая u(x,t)=X(x) T(t).

Тогда 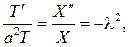и из граничных условий найдем

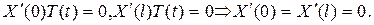
Собственные значения и собственные функции определяются из задачи

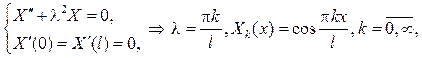
поэтому на этот раз смешанная задача решается рядом с неопределенны-

ми коэффициентами:

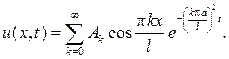
Подставляя этот ряд в начальное условие, будем иметь

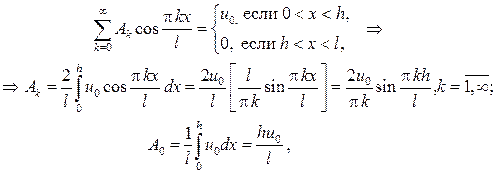
и следовательно окончательный ответ будет иметь вид

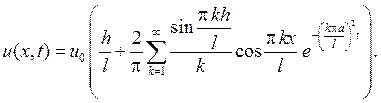
194. Дан однородный шар радиуса b, центр которого расположен в начале координат. Внешняя поверхность шара поддерживается при нулевой температуре, а начальная температура 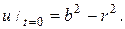Опреде-

лите температуру u(r,t) внутри шара при t>0.

Р е ш е н и е. Поставленная задача равносильна смешанной задаче

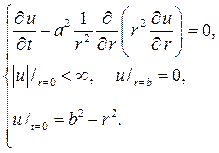
Следуя схеме метода Фурье, полагаем u(r,t)=R(r)T(t)и после подстанов-ки в уравнение получим

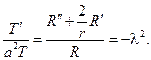
Из граничных условий будем иметь

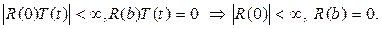
Следовательно, нужно решать задачу Штурма Лиувилля

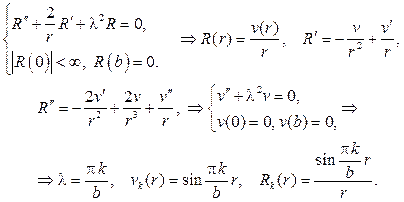
При решении уравнения 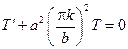найдем

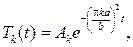
и тогда пишем ряд с неопределенными коэффициентами

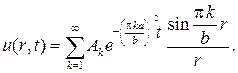
В силу начального условия будем иметь

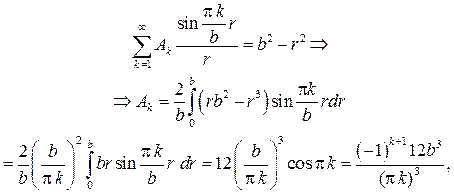
и стало быть ответ в задаче имеет вид

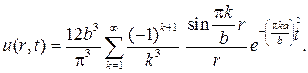
195. Найдите распределение температуры в однородном шаре радиуса b, внутри которого при t³0 действует источник тепла с постоянной плот- ностью q, а его поверхность поддерживается при нулевой температуре. Начальная температура во внутренних точках шара равна нулю.

Р е ш е н и е. Здесь нужно иметь дело со смешанной задачей:

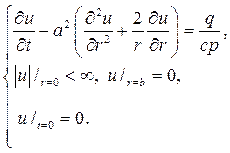
Функция 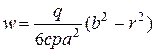есть решение дифференциального урав- нения, удовлетворяющее граничным условиям, поэтому после замены

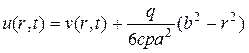
относительно новой функции v(r,t) придем к смешанной задаче

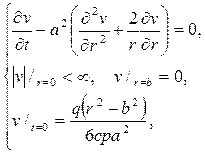
которая несущественно отличается от задачи 194. В итоге окончательно получим ответ:

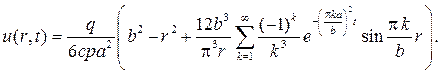
196. Найдите решение смешанной задачи

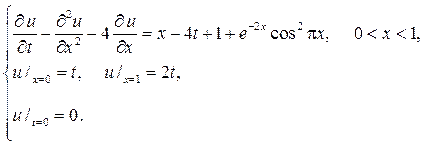
Р е ш е н и е. Непосредственно проверяется, что функция w=t(x+1) удовлетворяет уравнению и граничным условиям

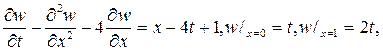
поэтому после замены u(x,t)=v(x,t) + t(x+1) относительно новой функции v(x,t) получим смешанную задачу

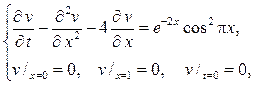
решение которой находится в виде ряда по собственным функциям зада- чи Штурма Лиувилля:

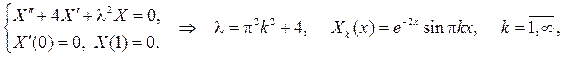
Подставляя ряд 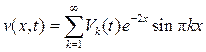в уравнение, будем иметь

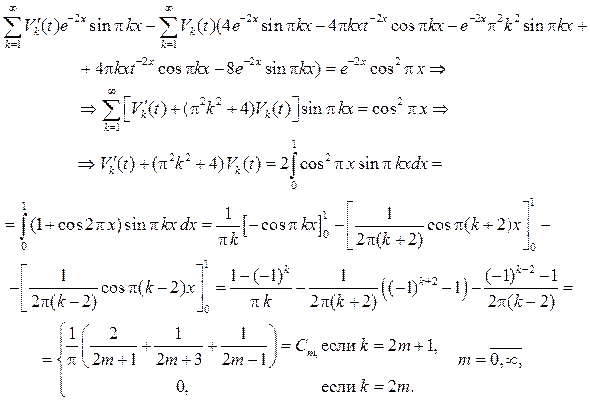
К полученным дифференциальным уравнениям для функций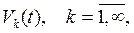

нужно присоединить условие 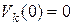.Получим семейство задач Коши:

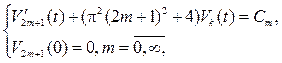
откуда находим 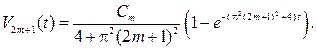Для четных k=2m все будут равными нулю, и, следовательно, придем к отве- ту:

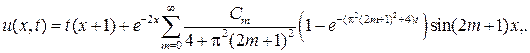
где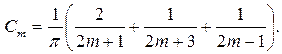

197. Сфера радиуса b содержит растворенное вещество с начальной концентрацией u₀ . Концентрация на поверхности сферы поддерживается постоянной, равной u₁>u₀. Найдите количество абсорбированного вещества в момент времени t>0.

198. Решите задачу об остывании однородного стержня длиной l с тепло- изолированной боковой поверхностью, если его начальная температура u(x,0)=l-x, концевая точка x=0 теплоизолирована, а x=l поддерживается при постоянной температуре.

199. Дан тонкий однородный стержень длиной l, начальная температура которого равна нулю. На конце x=l поддерживается нулевая темпера- тура, а на конце x=0 температура растет линейно со временем, так что u(0,t)=At, где A – константа. Найдите распределение температуры u(x,t) при t>0.

Решите следующие смешанные задачи

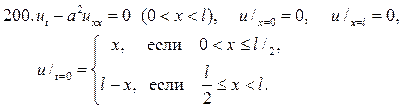
201.

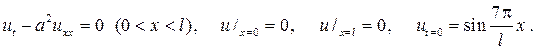
202.

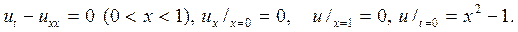
203.

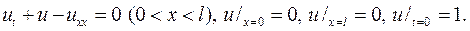
204.

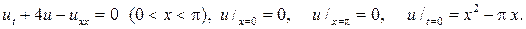
205.

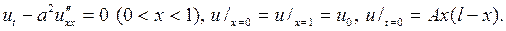
206.

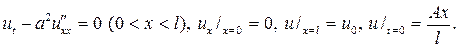
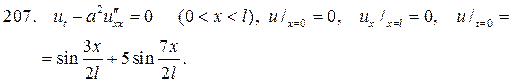
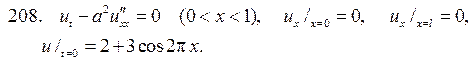
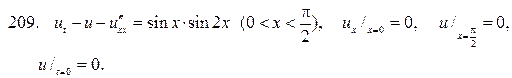
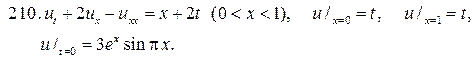
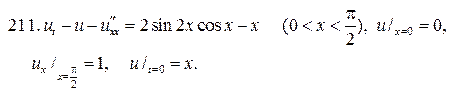
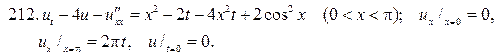
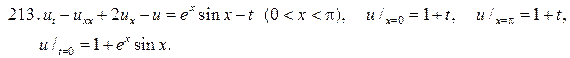
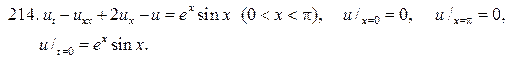
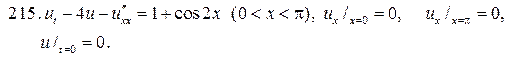
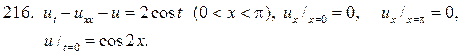
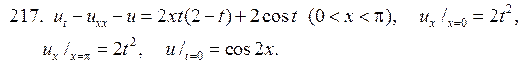
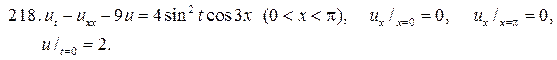
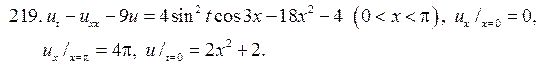
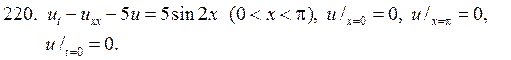
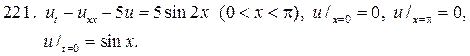
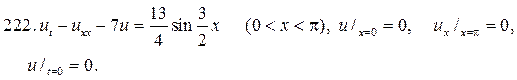
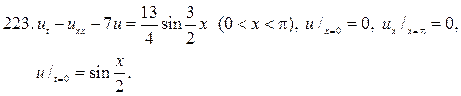
224.

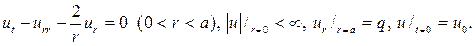
225.

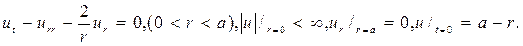
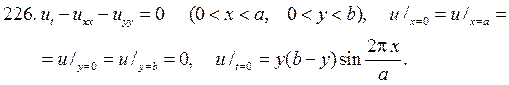
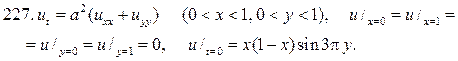
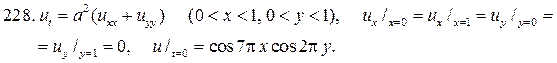
§ 7. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ

И РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ

ДЛЯ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО

И ПАРАБОЛИЧЕСКОГО ТИПОВ

Дифференциальное уравнение 2-го порядка

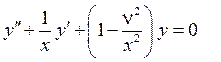(65)

принято называть уравнением Бесселя порядка v или уравнением цилин- дрических функций. Здесь 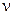есть произвольное действительное или ком-плексное число,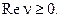

Если 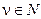, то общее решение уравнения (65) есть линейная комбина- ция

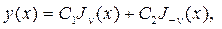(66)

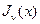где и 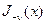называются соответственно цилиндрическими функ- цииями Бесселя первого и второго рода, для которых имеются представ- ления в виде рядов

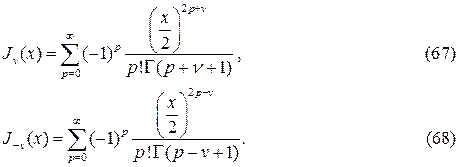
Если v=n, n=0,1,2,… , то функция J_n(x) и J_-n(x) линейно зависимы, что можно установить посредством соотношений (67),(68). В этих обстоят- ельствах для представления общего решения употребляются цилиндриче- ские функции Вебера-Неймана:

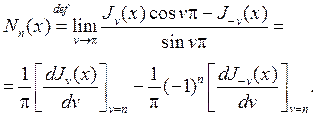
Функция N_n(x) линейно независима от J_n(x), для нее имеется представ-

ление в виде ряда

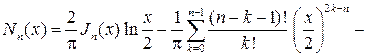
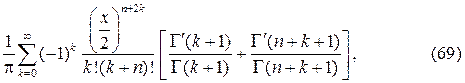
из которого видно, что функция Вебера-Неймана не ограничена в окрест- ности точки х=0. Вместо соотношения (66) при v=n общее решение урав- нения (65) берется в виде

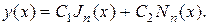(70)

Цилиндрические функции Бесселя с соседними индексами и их произ- водные связаны между собой рекуррентными соотношениями

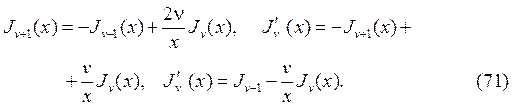
Отметим важный частный случай второй из формул (71) при v=0

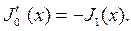(72)

Третье из соотношений (72) может быть записано в интегральной форме

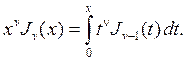(73)

Наиболее часто употребляются цилиндрические функции с целыми

индексами J₀(x), J₁(x), …, J_n(x), …, а также положительные нули этих функций. Всякое уравнение J_n(x)=0 имеет счетное множество положи- тельных корней:

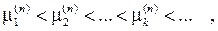
или, что то же самое, функция J_n(x)имеет счетное множество положи- тельных нулей. Приведём вычисленные с точностью до четырех десятич- ных знаков значения первых шести нулей функции J₀(x):

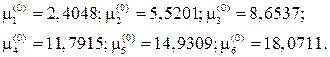
Вспомним, что если коэффициент k(х) обращается в нуль при х=0, то появляется так называемый особый случай постановки задачи Штурма Лиувилля (сравните (61 62)):

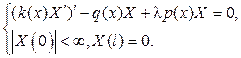(74)

Уравнение (65) может быть записано в эквивалентной форме:

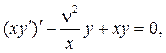(75)

и естественно, что оно соответствует особому случаю постановки крае-вых задач, когда k(x)=x, k(0)=0.

Простейшая краевая задача для уравнения Бесселя возникает при изу- чении собственных колебаний круглой мембраны:

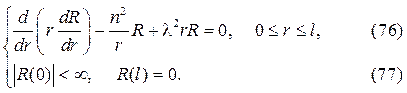
Здесь k(r)=r и весовая функция p(r)=r. Чтобы ее решить, полагаем x=λr, где x новая независимая переменная. Тогда

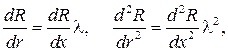
и уравнение (76) приводится к уравнению Бесселя

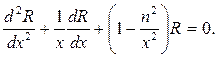
Общее решение этого уравнения представим формулой (70), а после возвращения к переменной r получим общее решение уравнения (76) в виде

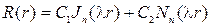(78)

Из (77) и (79) ясно, что J_n(0)=0, N_n(0)=∞, поэтому выполнимость первого из граничных условий (77)

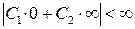
означает, что С₂=0.Тогда полагаем С₁=1, и со второго граничного усло- вия находим собственные значения

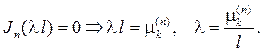
Соответственно из (78) найдем собственные функции

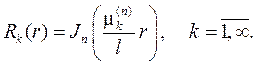(79)

Найденные собственные функции образуют ортогональную систему с весом r на отрезке [0,l], т.е. выполнено условие ортогональности

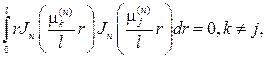
и можно рассматривать ряды Фурье по системе (79):

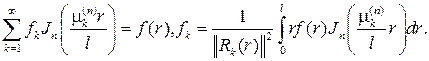
Квадрат нормы собственной функции вычисляется точно и имеет значение

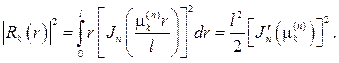(80)

Отметим также частный случай (см. (42))

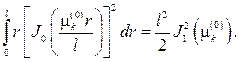(81)

Довольно часто встречается и вторая краевая задача для уравнения Бесселя

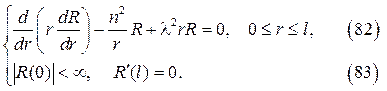
И на этот раз общее решение уравнения (82) может быть записано в ви-

де (78), снова получим С₂=0 и С₁=1, а собственные значения будут определяться из условия

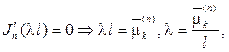
где через 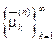обозначены положительные нули производной 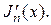Собственные функции задачи (82 83) будут записаны в виде

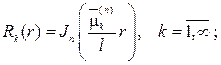
они образуют ортогональную систему с весом r на [0, l], а квадрат нормы

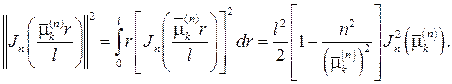
229. Решите задачу о свободных колебаниях однородной круглой мемб- раны радиуса l, закрепленной по краю, если начальная скорость равна ну- лю, а начальное отклонение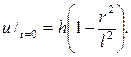

Р е ш е н и е. Здесь нужно решать смешанную задачу

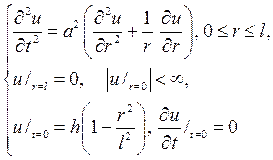
по методу Фурье, полагая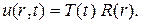

После подстановки в дифференциальное уравнение и разделения переменных придем к равенству

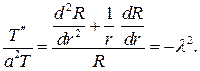
Из условия 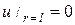найдем R(l)=0, а второе условие как в особом случае 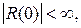поэтому придем к задаче Штурма Лиувилля:

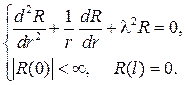
Вводя новую переменную 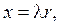будем иметь

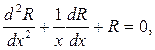
и его общее решение (см.(35))

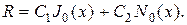
Возвращаясь к переменной r, получим общий вид радиальной функции:

Из условия 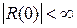найдем

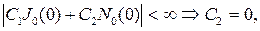
тогда полагаем 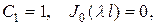откуда

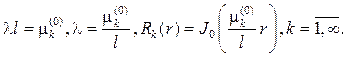
Для временной функции T(t) имеем дифференциальное уравнение с постоянными коэффициентами

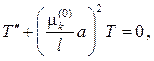
и его решение есть линейная комбинация

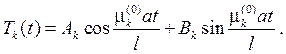
Умножая ее на собственную функцию и суммируя по всем k , получим ряд

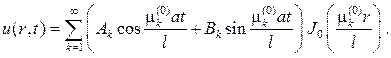
Из второго начального условия получим

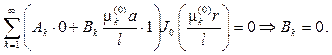
Первое начальное условие приводит к равенству

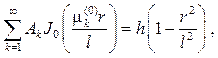
откуда с учетом (81) найдем (см.также (73))

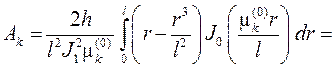
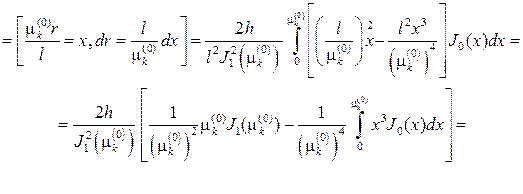
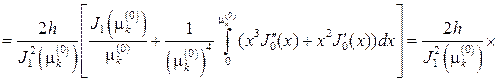
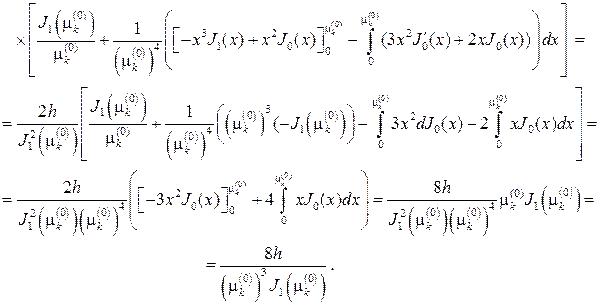Подставляя найденные коэффициенты в ряд, придем к ответу

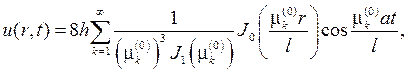
где 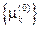положительные корни уравнения J₀(x)=0.

230 Решите задачу о свободных колебаниях круглой мембраны радиуса l, закрепленной по краю и колеблющейся в среде, сопротивление которой пропорционально скорости, если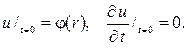

Р е ш е н и е. Здесь нужно решать смешанную задачу

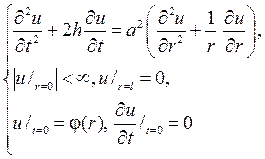
методом Фурье, полагая u(r,t)=R(r)T(t). Тогда после разделения перемен-

ных в дифференциальном уравнении

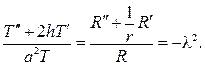
С учетом граничных условий придем к задаче Штурма Лиувилля для

радиальной функции

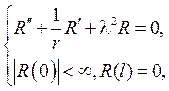
и ее собственные значения и собственные функции, как и в предыдущей задаче, соответственно равны

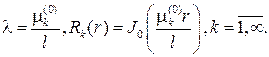
Дифференциальное уравнение для временной функции при малом h

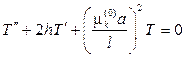
имеет решение

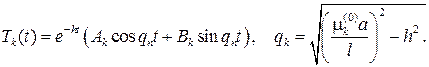
Составляем ряд

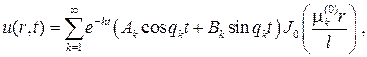
и подставляя его в начальное условие 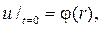придем к равенству

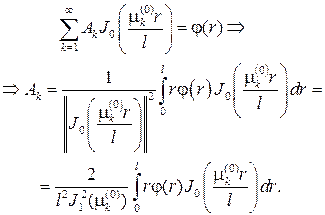
Из второго граничного условия вытекает, что

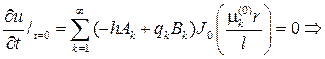
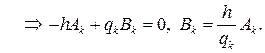
В итоге придем к ответу

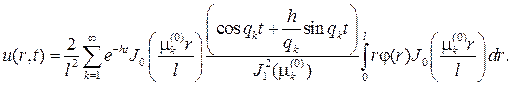
231. Уравнение малых продольных колебаний нити, подвешенной в кон- цевой точке x=l и колеблющейся под действием силы тяжести, имеет вид

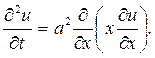
Найдите u(x,t) при t>0если

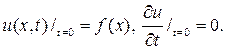
Р е ш е н и е. Здесь возникает смешанная задача

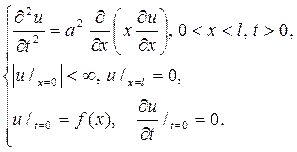
Полагая u(x,t)=X(x)T(t) придем к соотношению

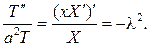
С учетом граничных условий, придем к задаче Штурма Лиувилля

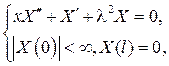
ее собственные функции ортогональны с единичным весом на [0, l]. Вве- дя новую переменную 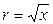, найдем

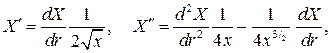
соответственно преобразуется и задача Штурма Лиувилля

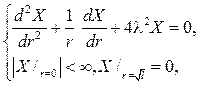
а ее собственные значения и собственные функции соответственно бу- дут

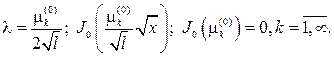
Дифференциальное уравнение для временной функции

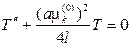имеет решение

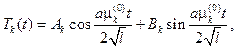
поэтому составляем ряд

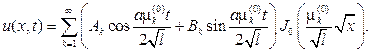
Подставляя его в первое начальное условие, найдем

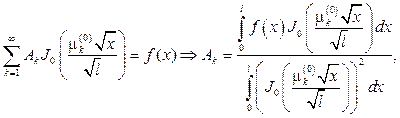
причем для интеграла, стоящего в знаменателе, верно равенство

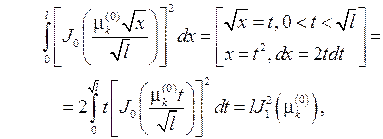
следовательно, окончательно имеем

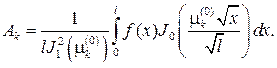
Из второго начального условия вытекает, что B_k=0, поэтому в ответе получим

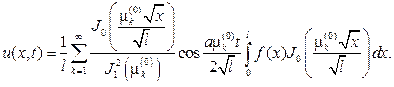
232.Круглая однородная мембрана радиуса l закреплена по краю, нахо- дится в состоянии равновесия при натяжении Т₀. Найдите отклонение мембраны u(r,t) от положения равновесия, если к ней прилагается равно- мерно распределенная нагрузка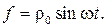

Р е ш е н и е. Текстовая задача равносильна смешанной задаче

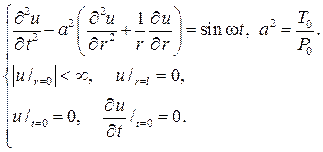
Найдем решение имеющегося дифференциального уравнения в виде

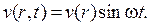
Относительно v( r ) будем иметь обыкновенное дифференциальное урав- нение

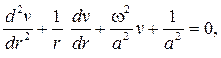
частным решением которого будет, что нетрудно проверить, функция

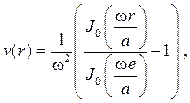
и это частное решение удовлетворяет граничным условиям