Теоретические сведения и примеры. В настоящем разделе рассмотрены некоторые методы решения систем алгебраических

В настоящем разделе рассмотрены некоторые методы решения систем алгебраических уравнений. Разумеется, это не все возможные методы, но, тем не менее, авторы посчитали нужным добавить такой раздел в пособие, поскольку умение решать системы уравнений требуется и при решении текстовых задач, и при решении задач на прогрессии, а также в некоторых других случаях.

Системой kуравнений с n неизвестными называется

k уравнений, в каждом из которых неизвестные, обозначенные одной и той же буквой, означают одну и ту же неизвестную величину.

Решением системы kуравнений с nнеизвестными называется всякий упорядоченный набор из n таких чисел, которые, будучи подставлены в систему вместо неизвестных, обращают каждое уравнение системы в тождество.

Мы можем решить систему уравнений, т. е. найти множество всех ее решений, или показать, что она решений не имеет.

Если система алгебраических уравнений имеет решение, то оно не обязательно единственное. Множество решений системы может быть конечным или бесконечным.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Система называется определенной, если она имеет конечное число решений, и неопределенной, если она имеет бесконечное множество решений.

Две системы называются равносильными, если они имеют одно и то же множество решений.

Как правило, наиболее простыми являются системы линейных уравнений, в которых неизвестные встречаются только в первой степени.

Система вида 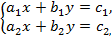где а₁, а₂, b₁, b₂, c₁, c₂ – некоторые известные числа, называется линейной системой двух уравнений с двумя неизвестными. Аналогично определяются системы линейных уравнений с большим числом неизвестных.

Одним из методов решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных (метод Гаусса).

Пример 1. Решить систему уравнений:

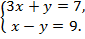
Решение. Из второго уравнения выразим x и подставим в первое. Получаем:

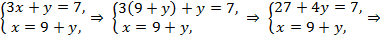
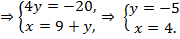
Ответ: (4,–5).

Пример 2. Решить систему уравнений:

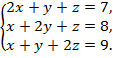
Решение. Решим данную систему методом последовательного исключения неизвестных. Перепишем систему в другой, более удобной для нас последовательности, поменяв местами первое и третье уравнения: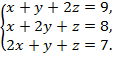

Теперь поступим так: первое уравнение оставим без изменения, из второго уравнения вычтем первое, а из третьего уравнения вычтем первое, умноженное на два. В результате получим: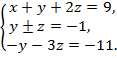

Теперь второе и третье уравнения системы содержат только два неизвестных. Оставив без изменения первые два уравнения последней системы, прибавим к третьему уравнению второе: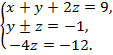

Из последнего уравнения находим z, подставляем полученное значение во второе уравнение и находим y, а затем из первого уравнения – значение x: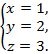

Ответ: x = 1; y = 2; z = 3.

Замечание. Более привычным этот метод выглядит, когда мы из какого-либо одного уравнения системы выражаем одно неизвестное через остальные, в результате чего в последующих уравнениях оказывается на одно неизвестное меньше.

Аналогично, выражая одно неизвестное через другие, можно решать и системы нелинейных уравнений. Но в некоторых случаях такая подстановка приводит к уравнениям высоких степеней, решить которые затруднительно. Поэтому можно рассмотреть другие методы.

Для решения систем нелинейных алгебраических уравнений часто используется метод введения новых переменных. Тогда система сводится к более простой, которую и требуется решить.

Пример 3.Решить систему уравнений:

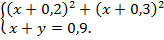
Решение. Пусть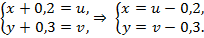

Теперь данная система нелинейных алгебраических уравнений будет записана следующим образом:

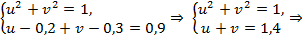
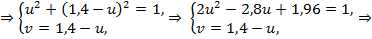
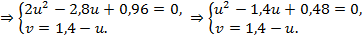
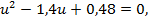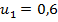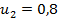Квадратное уравнение имеет два корня, и , следовательно, получаем два варианта решения системы: 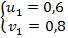или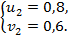

В первом случае 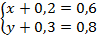откуда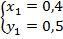

А во втором случае 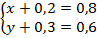откуда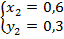

Ответ: 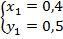или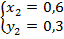

Пример 4.Решить систему уравнений:

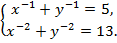
Решение.Перепишем систему уравнений в виде:

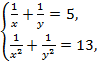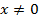где и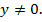

Приводя уравнения к общему знаменателю, получаем,

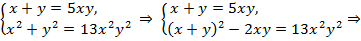
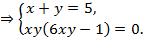
Последняя система равносильна двум системам уравнений:

1) 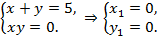Это решение не удовлетворяет условию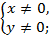

2)

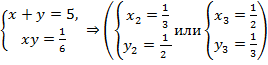
Ответ: 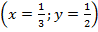или .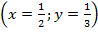

Замечание. Аналогично предыдущему примеру в системе можно было сделать замену переменных по следующему правилу: .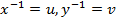

Тогда бы система с новыми переменными имела вид

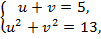откуда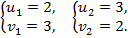

Обратная замена приводит к окончательному результату.

Пример 5. Решить систему уравнений:

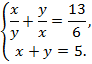
Решение: ОДЗ: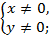

Обозначим 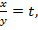тогда 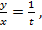причём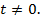

Первое уравнение системы примет вид: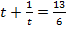

или .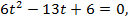

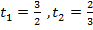Для значения 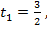получим систему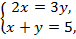

а для значения 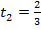систему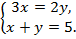

Решая эти системы, получим окончательный результат:

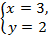или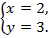

Ответ: х = 2 и у = 3 или х = 3 и у = 2.

Замечание. Можно было не вводить новую переменную, а решить непосредственно данную систему. Умножив левую и правую часть первого уравнения на 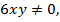получим:

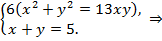
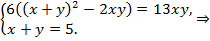
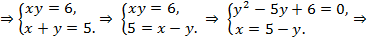
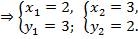
Пример 6.Решить систему уравнений:

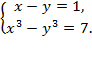
Решение. Преобразуем второе уравнение системы и получим:

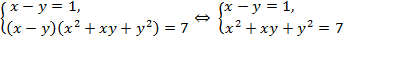
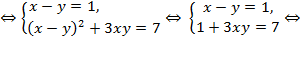
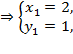или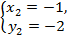

Ответ: {2; 1}, {–1; –2}.

Пример 7. Решить систему уравнений:

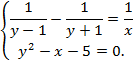
Решение. ОДЗ: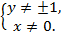

Преобразуем первое уравнение системы:

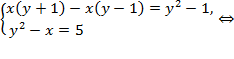
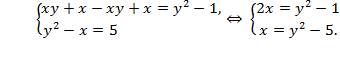
Подставив значение 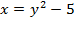в первое уравнение системы, получим

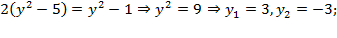тогда

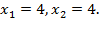
Ответ: {4; 3}, {4; –3}.

Пример 8. Решить систему уравнений:

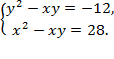
Решение. Из условия имеем 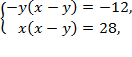причем ни один из сомножителей в левой части уравнений не равен нулю, поскольку правая часть отлична от нуля. Разделив первое уравнение на второе, получим:

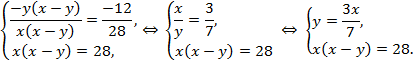
Подставив 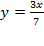из первого уравнения системы во второе, получим: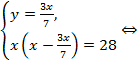

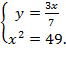
Отсюда возможны два варианта:

1)

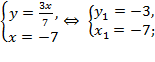
2)

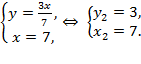
Ответ: х = –7 и у = –3 или х = 7 и у = 3.

Пример 9.Решить систему уравнений:

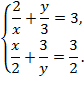
Решение. Допустимые значения переменных: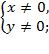

Приводя уравнения системы к общему знаменателю, получаем :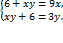

Вычтем из первого уравнения второе:

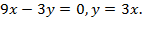
Отсюда получаем 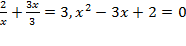при .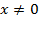

Корни квадратного уравнения: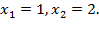

Тогда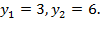

Ответ: 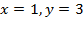или