Тема 4. Системы векторов. N-мерное векторное пространство. Евклидово пространство

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

«Камская государственная инженерно-экономическая академия»

ЛИНЕЙНАЯ АЛГЕБРА

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

для студентов заочной формы обучения

Г. Набережные Челны

Цель и задачи дисциплины, её место в учебном процессе.

Цельпреподавания дисциплины «Линейная алгебра» -формирование системы базовых знаний по данной дисциплине, которая позволит будущим специалистам решать в своей повседневной деятельности актуальные задачи практики, понимать написанные на современном научном уровне результаты других исследований и тем самым совершенствовать свои профессиональные навыки.

Основнымизадачами дисциплиныявляются:

- ознакомление студентов с ролью математики в современной жизни, с характерными чертами математического метода изучения реальных задач;

- обучение студентов теоретическим основам курса;

- привитие практических навыков математического моделирования реальных социально-экономических задач с использованием математического аппарата данного курса;

- развитие у студентов навыков творческого и логического мышления, повышение общего уровня математической культуры.

Данная дисциплина является основой при изучении таких дисциплин, как «Численные методы», «Теория вероятностей и математическая статистика», «Многомерные статистические методы», «Методы оптимизации», «Исследование операций», «Эконометрика», а также других дисциплин, изучающих современные экономико-математические методы. В свою очередь, для изучения данной дисциплины необходимо знание элементарной математики.

В результате изучения данной дисциплины студент должен:

- знать теоретические основы линейной и векторной алгебры, алгебры многочленов, аналитической геометрии;

- уметь использовать полученные знания для решения практических задач.

Изучение дисциплины предусматривает проведение лекционных, практических занятий и самостоятельную работу студентов. В лекциях излагается содержание тем программы с учётом требований, установленных для специалиста в квалификационной характеристике. Практические занятия проводятся с целью закрепления теоретических основ курса, получения практических навыков решения математических задач. Контроль знаний осуществляется с помощью контрольной работы и итогового экзамена.

Содержание и структура дисциплины.

Содержание дисциплины (наименование и номера тем).

Раздел I. ЛИНЕЙНАЯ АЛГЕБРА.

Тема 1. Определители.

Определители 2-ого, 3-его, порядков, порядка n. Свойства определителей. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца. Вычисление определителей.

Литература: [1] –C.142-154; [2] – C.22-26; [3] – C.426-431; [4] – C.263-268.

Тема 2. Матрицы.

Определение матрицы. Виды матриц. Действия над матрицами. Линейная зависимость и независимость строк матрицы. Базисный минор. Ранг матрицы. Обратная матрица, условие существования, основные способы её нахождения. Матричные уравнения, их решение.

Литература: [1] –C.136-142; 159-165;174-182; [2] – C.9-16; 26-29;

[3] – C.416-426; 431-435; [4] – C.259-263; 272-276.

Тема 3. Системы линейных уравнений.

Системы линейных уравнений (СЛУ). Основные понятия и определения. Матричная запись СЛУ. Теорема Кронеккера-Капелли. Формулы Крамера. Решение СЛУ методом обратной матрицы. Решение СЛУ методом Гаусса. Базисные и свободные неизвестные. Общее, базисное и опорное решения СЛУ. Однородные системы линейных уравнений, свойства их решений. Условия существования ненулевых решений однородных СЛУ. Фундаментальная система решений. Структура общего решения СЛУ.

Литература: [1] –C.136-142; 154-159; 165-174; [2] – C.38-53;

[3] – C.436-457; [4] – C.268-276.

Тема 4. Системы векторов. N-мерное векторное пространство. Евклидово пространство.

N – мерный арифметический вектор. Линейные операции над векторами, их свойства. Понятие n-мерного векторного пространства 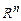. Линейно зависимые и независимые системы векторов, их свойства. Базис и ранг системы векторов, пространства 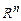. Координаты вектора в 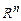. Скалярное произведение. Евклидово пространство. Ортогональный базис. Разложение вектора по ортогональному базису. Процесс ортогонализации Шмидта.

Литература: [1] –C.188-196; 222-231; [2] – C.68-78; [3] – C.406-416.