Последний взлёт и падение

Сосредоточивший в своих руках всю власть Бонапарт назначил Монжа пожизненным сенатором, в Политехнической школе он читает курсы приложения алгебры и анализа к геометрии^[7][8], составляет устав и план работы школы. В августе 1803 года Монж назначен вице-президентом Сената, а в сентябре — сенатором Льежа с поручением организовать там производство пушек. Преданность новой власти и заслуги перед Империей были вознаграждены — он получил высшую степень ордена Почетного легиона, в 1806 году назначен президентом Сената на очередной годичный срок, ещё через год получил титул графа Пелузского и 100 000 франков для покупки имения. Однако вскоре его начало подводить здоровье, у него на время отнялась рука. Монж прекращает преподавание в Политехнической школе, но продолжает научную работу и консультирует предлагаемые технические проекты. Так, в 1805 году император поручает ему изучить возможность проведения канала от реки Урк для снабжения Парижа водой. В 1808 году его привлекли к оценке возможности десанта в Англию на 100 больших аэростатах, каждый из которых должен был поднимать 1000 солдат и снаряжение для них.

События 1812—1814 гг. закончились поражением Франции и ссылкой Бонапарта. Монж оставался приверженцем Империи и в период всех Ста дней по-прежнему был на стороне Бонапарта. После восстановления власти Бурбонов Монж был лишён званий, наград и пенсии, исключён (правда, всего лишь на год) из Политехнической школы. Распоряжением правительства в 1816 году он и Карно были исключены из преобразованного на новый лад Института и замещены Коши и Брегетом. Как один из «цареубийц», Монж мог ждать и более серьёзных репрессий. От всех этих ударов судьбы, довершённых ссылкой его зятя Эшассерио, как бывшего члена Конвента, Монж заболел и вскоре скончался. Его похоронили на кладбище Пер-Лашез. Жена Монжа пережила его на 24 года.

Научная деятельность

Монж - творец новой науки

Переходим к рассмотрению классического творения Монжа: «Geometrie descriptive» («Начертательная геометрия»). Книгой этой Монж свел в стройную научную систему весь разрозненный многообразный материал. Новая его научная система привела к полной возможности выполнять на плоской поверхности листа чертежной бумаги посредством планиметрических построений решение конструктивных задач стереометрии евклидовскими чертежными инструментами: циркулем и линейкой.

Если бы мы пожелали задачу в пространстве трех измерении решать непосредственно в таком пространстве, то мы, прежде всего, встретились бы с непреодолимым препятствием в отношении чертежных инструментов. «Начала» Евклида рассматривают такие построения, считая возможным каким-то непонятным способом строить в пространстве трех измерений плоскость любого положения, поверхность цилиндра и конуса вращения и шаровую поверхность. Однако Евклид нигде не дает указаний, какими же «чертежными» инструментами возможно осуществить эти элементарные построения, к которым он сводит все другие сложные построения. Если же обратиться к его циркулю и линейке, то окажется, что мы лишены возможности сделать даже более элементарные построения, как-то фиксировать в пространстве точку, провести через нее прямую линию или плоскость.

Гаспар Монж свел невозможные фактически «чертежные» построения в пространстве трех измерений к действиям над двумя ортогональными проекциями какого-либо тела, получаемыми на двух, неизменно связанных между собою, взаимно перпендикулярных координатных плоскостях, служащих плоскостями проекций. Неизменная связь достигается неизменной постоянной по положению в пространстве линией пересечения этих плоскостей проекций. Таким образом, в начертательной геометрии Монжа впервые появляется ось проекций, которая до него не была известна. Для того же, чтобы весь чертеж, состоящий из двух проекций, располагался на одном плоском листе бумаги, Монж, посредством вращения плоскостей проекций вокруг их линии пересечения, развертывает эти плоскости, совмещая их в одну плоскость. Однако названия «оси проекции» он не упоминает на протяжении всего своего курса, называя ее всегда линией пересечения плоскостей проекций. При изложении курса перспективы он вводит термин «Iigne de terre», не встречаемый в «Geometric descriptive».

Отметим при этом, что плоский чертеж — не выдумка Монжа, а принудительное естественное условие. Стереометрические задачи в пространстве трех измерений можно решать только умозрительно. Практически же мы вынуждены прибегать к поверхности двух измерений.

Архитекторы древности и средневековья делали это на земле, на песке и на самом строительном материале, на полу, на стенах и т. п.

Монж, анализируя различные практические приемы, применяемые в строительном деле, отделил элементы теории и разработал стройную логическую научную систему построения в проекциях различных основных задач на прямую линию, плоскость и др. Он говорил: «Кто совсем свободно знает прямую и плоскость, тот не встретит затруднений в начертательной геометрии».

На основании разработанной Монжем общей геометрической теории все вопросы прикладного характера находили решение, и даже такие, которые до этого считались неразрешимыми. Оказалось возможным не прибегать к изготовлению моделей, которые до того времени являлись неотъемлемой составной частью строительного проекта. Сам Монж в качестве ученика испытал на себе в Мезьерской школе эту практику «гипсового училища», как иронически называли вспомогательное отделение школы.

М. Шаль, рассматривая прикладную сторону, говорит: «Понятно, что. .. начертательная геометрия должна была бы существовать во все времена. И в самом деле, мастера каменного дела и плотники всегда определяли и набрасывали рисунки на плоскости — формы тех тел о трех измерениях, которые приходилось им строить. Было даже несколько руководств, и хороших..., тем не менее приурочить практические вопросы к необходимому числу отвлеченных и элементарных действий никому не приходило в голову, а в особенности собрать их все в одно руководство с самостоятельным заглавием, с тем, чтобы придать им характер учения, независимо от практических навыков, из ряда которых они достаточно уже вышли. Это задумал и выполнил с редким талантом Монж».

Так оценил новую науку французский математик М. Шаль в своей вступительной речи к курсу высшей геометрии, читанной в Парижском факультете наук 23 декабря 1846 г. Шаль считает, что Монж и Карно «оживили во Франции дух геометрического метода и вдохновили молодых математиков, которые вскоре пошли по этому пути».

Создание «Начертательной геометрии» послужило началом и основой работ, позволивших новой Европе овладеть геометрическими знаниями Древней Греции; работы же по теории поверхностей, помимо своего непосредственного значения, привели к выяснению важногопринципа непрерывности и к раскрытию смысла той обширной неопределенности, которая возникает при интегрировании уравнений с частными производными, произвольными постоянными и тем более с появлением произвольных функций.

Принцип непрерывности в том виде, в каком он сформулирован Монжем, может быть изложен следующим образом. Всякое свойство фигуры, выражающее отношения положения и оправдывающееся в бесчисленном множестве непрерывно связанных между собой случаев, может быть распространено на все фигуры одного и того же рода, хотя бы оно допускало доказательство только при предположении, что построения, осуществимые не иначе как в известных пределах, могут быть произведены на самом деле. Такое свойство имеет место даже в тех случаях, когда вследствие полного исчезновения некоторых необходимых для доказательства промежуточных величин предполагаемые построения не могут быть произведены в действительности.

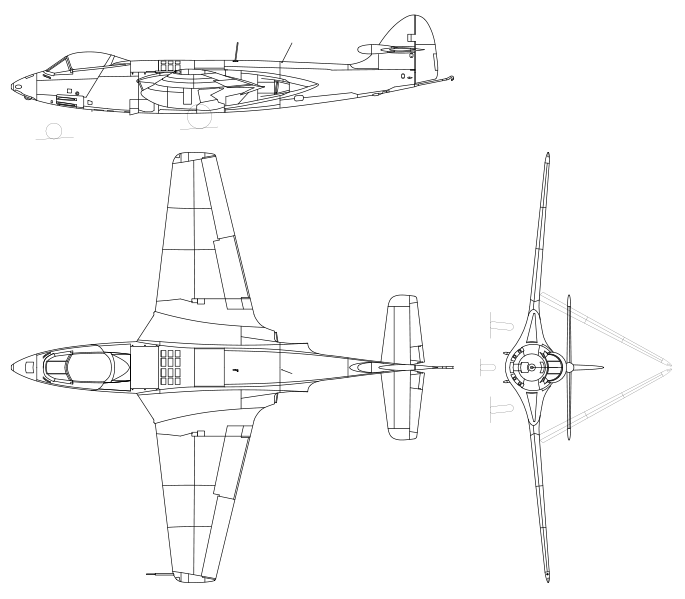
Самолёт Hawker Sea Hawk, изображённый с помощью эпюра Монжа

Из других, менее значительных вкладов Монжа в науку следует назвать теорию полярных плоскостей применительно к поверхностям второго порядка; открытие круговых сечений гиперболоидов и гиперболического параболоида; открытие двоякого способа образования поверхностей этих же тел с помощью прямой линии; создание первого представления о линиях кривизны поверхностей; установление начал теории взаимных поляр, разработанной впоследствии Понселе, доказательство теоремы о том, что геометрическое место вершины трёхгранного угла с прямыми плоскими углами, описанного около поверхности второго порядка, есть шар, и, наконец, теорию построения ортогональных проекций трехмёрных объектов на плоскости, получившую название эпюр Монжа.

Многочисленные мемуары Монжа издавались в трудах парижской и туринской академий, выходили в «Journaux de l’Ecole Polytechnique et de l’Ecole Normale», в «Dictionnaire de Physique», «Методической энциклопедии» Дидро и д’Аламбера, в «Annales de Chimie» и в «Décade Egyptienne», издавались отдельно: «Dictionnaire de Physique» (1793—1822), составленный при сотрудничестве Кассини, «Avis aux ouvriers en fer sur la fabrication de l’acier» (1794), составленный вместе с Бертолле, и др. В ней содержатся библиография трудов Монжа (72 наим.) и перечень публикаций о его жизни и деятельности (73 наим.).

Имя Гаспара Монжа внесено в список 72 величайших учёных Франции, помещённый на первом этаже Эйфелевой башни.