Определения и обозначения, используемые в работе

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение

Высшего образования

БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ АКАДЕМИКА И.Г. ПЕТРОВСКОГО»

(БГУ)

Естественно-научный институт

Физико-математический факультет

Кафедра алгебры и геометрии

Реферат

«Операторные группы»

Выполнила:

магистрантка 1курса 2 группы

направления 01.04.01 «Математика»

Корочкина Г.О.

Научный руководитель:

кандидат физико-математических наук, доцент Сорокина М.М.

Брянск – 2016 г.

Содержание

Введение. 3

Глава 1. Предварительные сведения. 4

1.1. Определения и обозначения, используемые в работе. 4

1.2. Используемые результаты.. 5

Глава 2. Операторные группы.. 6

2.1. Основные понятия, связанные с операторными группами. 6

2.2. Централизаторы и нормализаторы секций конечной группы.. 7

2.3. Основные свойства операторных групп. 9

Заключение. 13

Список литературы.. 14

Введение

Математика играет огромную роль в нашем обществе. Одной из областей математики является теория групп. Большая и длительная работа математиков была необходима для создания этой теории.

Данная теория начала свое развитие благодаря трем составляющим: теории уравнений, теории чисел и геометрии. Создателем теории групп является французский математик Эварист Галуа. Понятие группы возникло в результате формального описания симметрии и эквивалентности геометрических объектов, которое использовал в своей теории Э. Галуа. Данное описание дало начало понятию группы. Почти все структуры общей алгебры - частные случаи групп.

Первыми математиками, которые оценили важность теории групп, стали Артур Кэли и Огюстен Луи Коши. Современное определение понятия «группа» было дано в 1882 году Вальтером фон Дюком. Ощутимый вклад в теорию групп внесли такие математики, как Артин, Э. Нётер, Л. Силов, О.Ю. Шмидт, А.Г. Курош, С.А. Чунихин, С.Н. Черников и многие другие.

В настоящее время теория групп представляет собой хорошо развитую область математики. Каждый год проходят международные конференции, посвященные теории конечных и бесконечных групп. Хорошо развитые научные школы, занимающиеся теорией групп, функционируют в Москве, Санкт-Петербурге, Екатеринбурге, Новосибирске, Омске, Томске, Иркутске, Челябинске, Красноярске и других городах России.

Данная работа посвящена операторным группам, которые занимают важное место в современной теории конечных групп.

Реферат состоит из введения, двух глав, списка используемой литературы и заключения. В главе 1 приводятся некоторые предварительные сведения, используемые в работе. Основное содержание реферата представлено в главе 2. В ней изучаются основные примеры и свойства операторных групп.

Глава 1. Предварительные сведения

Определения и обозначения, используемые в работе

Определение 1.1.1. Непустое множество G с определенной на ней бинарной алгебраической операцией называется группой, если выполняются следующие аксиомы (аксиомы группы):

1) ассоциативность операции на G;

2)

3) .

Определение 1.1.2. Группа называется абелевой, если операция коммутативна на , т.е. .

Определение 1.1.3.Непустое подмножество Н группы G называется подгруппой группы G и обозначается , если является группой относительно той же операции, что и группаG.

Определение 1.1.4. Подгруппа группы называется нормальной подгруппой и обозначается , если выполняется такое равенство .

Определение 1.1.5. Подгруппа группы называется нормальной, если .

Определение 1.1.6. Правым смежным классом группы 𝐺 по подгруппе 𝐻 с представителем называется множество . Аналогично определяется левый смежный класс группы 𝐺 по подгруппе 𝐻 с представителем .

Определение 1.1.7. Произведением подгрупп 𝐻 и 𝐾 группы G называется множество .

Определение 1.1.8. Нормальная подгруппа группы G называется минимальной и обозначается если или .

Определение 1.1.9. Пусть группа, , – группа.

1. Нормализатором подмножества в группе G называется множество всех элементов группы G, перестановочных с H в целом и обозначается , т.е.

2. Централизатором подмножества H в группе G называется множество всех элементов группы G, перестановочных с H поэлементно и обозначается , т.е.

Определение 1.1.10. Отображение группы в группу называется гомоморфным отображением или гомоморфизмом, если .

Определение 1.1.11. 1) Инъективный гомоморфизм в называется мономорфизмом

2) Биективный гомоморфизм на называется автоморфизмом.

3) Гомоморфизм в называется эндоморфизмом.

Обозначение 1.1.1. 1) – множество всех автоморфизмом группы

2) – множество всех эндоморфизмов группы .

Определение 1.1.12. Пусть G – группа, – отображение, заданное по правилу: , где Тогда .

Определение 1.1.13. Центром группы называется множество всех центральных элементов группы и обозначается , т.е.

Определение 1.1.14. Пусть – группа, Подгруппа группы называется А-допустимой, если .

Определение 1.1.15. Подгруппа Н группы называется характеристической и обозначается если .

Определение 1.1.16. 1) Ряд (цепь) группы называется нормальным рядом (цепью), если .

2) Ряд (цепь) группы называется субнормальным рядом (цепью), если .

Определение 1.1.17. Подгруппа Н группы называется субнормальной подгруппой и обозначается , если является членом некоторого субнормального ряда группы G, т.е. если в G существует субнормальная -цепь.

Определение 1.1.18. 1) Нормальный ряд группы G без повторений членов называется главным рядом группы G, если он не допускает дальнейшего уплотнения нормальными подгруппами, т.е. .

2) Субнормальный ряд группы G без повторений членов называется композиционным рядом группы G, если он не допускает дальнейшего уплотнения субнормальными подгруппами, т.е. .

3) Фактор главного (композиционного ряда) называется главным (композиционным) фактором.

Определение 1.1.19. Группа G называется полупрямым произведением своих подгрупп А и В и обозначатся G=А 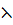В, если выполняются условия:

1) ;

2) ;

3) .

Используемые результаты

Теорема 1.2.1 (Свойства смежных классов).

Пусть группа, . Тогда справедливы следующие утверждения.

1) Любой элемент смежного класса может быть выбран в качестве его представителя, то есть , то ;

2) Любые два смежных класса либо совпадают, либо не пересекаются, то есть если , то ;

3) Мощность правого смежного класса совпадает с мощностью и совпадает с мощностью левого смежного класса , то есть ;

4) .

Лемма 1.2.2. Пусть группа, .Тогда:

1) ;

2) ;

3) ;

4) ;

5) .

Лемма 1.2.3 (Свойства примарных групп). Пусть – примарная группа.

1. Центр неединичной примарной группы отличен от 1, т.е. если то .

2. Если , то ,т.е. каждая собственная подгруппа примарной группы собственно содержится в своем нормализаторе.

3. Если , то и - простое число, т.е. все максимальные подгруппы примарной группы нормальны в и имеют простые индексы.

4. Если и , то .

5. Если , - простое число и .

Лемма 1.2.4. Пусть Тогда:

1) единичный элемент в соответственно;

2) ;

3) где ядро гомоморфизма ;

4) где ;

5) ;

6) .

Теорема 1.2.5. Если – гомоморфизм в , то .

Теорема 1.2.6. Если , то .

Лемма 1.2.7. 1) Если — главный ряд группы , то

2) Если — композиционный ряд группы , то — простая группа,

Теорема 1.2.8. (Жордана–Гёльдера). Любые два композиционных (главных) ряда группы изоморфны.

Теорема 1.2.9.(свойства характеристических подгрупп группы). Пусть – группа. Тогда справедливы следующие утверждения:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;