Методические указания к решению задачи № 1.3

В задаче № 1.3 рассматривается статически неопределимая конструкция, стержневые элементы которой работают на растяжение или сжатие и число неизвестных сил, приложенных к абсолютно жесткому брусу, превышает возможное число уравнений статики. Разность между числом неизвестных усилий и числом возможных уравнений статики определяет степень статической неопределимости системы:

,

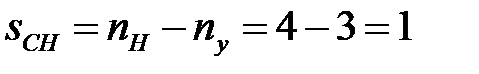где n_H – число неизвестных сил; n_y – число уравнений статического равновесия.

Уравнения, недостающие для определения усилий в стержнях, можно получить, рассматривая возможную деформацию системы. Условие, выражающее зависимость между деформациями отдельных элементов системы (конструкции), называется условием совместности деформаций. Оно получается из геометрических соотно­шений между дефор­мациями элементов конструкции. Используемые при решении задачи расчетные формулы приведены в методических указаниях к решению задач № 1.1 и 1.2 (см. раздел 2.3) .

Статически неопределимые конструкции рассчитывают, рассматривая совместно уравнения статической, геометрической и физической сторон задачи. При этом придерживаются следующего порядка:

1. Статическая сторона задачи. Составляются уравнения равновесия отсеченных элементов конструкции, содержащие неизвестные усилия. Определяется степень статической неопределимости.

2. Геометрическая сторона задачи. Рассматривая систему в деформированном состоянии, устанавливаются чисто геометрические связи между деформациями и перемещениями отдельных элементов конструкции и составляются уравнения совместности деформаций (уравнения совместности перемещений). Для получения этих уравнений используются прямой и обратный методы засечек (см. раздел 2.3).

3. Физическая сторона задачи. На основании закона Гука выражаются перемещения или деформации элементов конструкции через действующие в них неизвестные (пока) усилия.

4. Математическая сторона задачи (синтез). Решая совместно статические, геометрические и физические уравнения, находят неизвестные усилия.

Для определения температурных напряжений и монтажных усилий указанная схема расчета сохраняется. В этих случаях условия статики составляют только для усилий стержней.

Величины изменений длин нагретых или охлажденных элементов определяют алгебраическим суммированием приращений длин от усилий 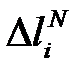и изменения температуры :

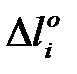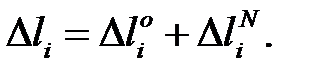
Абсолютное удлинение стержня от продольной силы определяется законом Гука

.

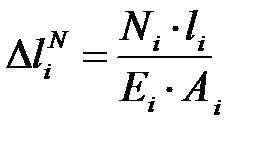Абсолютное удлинение стержня от изменения температуры Δt определяется зависимостью вида:

,

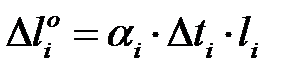где α_i - коэффициент температурного расширения.