Задания для самостоятельной работы. 1. Найдите уравнения координатных плоскостей аффинной системы координат
1. Найдите уравнения координатных плоскостей 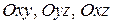 аффинной системы координат
аффинной системы координат 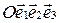 .
.
2. Могут ли числа а, в и с в уравнении плоскости «в отрезках» быть равными нулю одновременно? Почему? Может ли только одно (или два) равняться 0? Почему?
3. Какое из следующих уравнений является уравнением плоскости «в отрезках», а какое – не является и почему? Как привести его к виду «в отрезках»?
а) 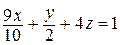 ; ; | в) 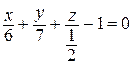 ; ; |
б) 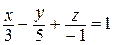 ; ; | г) 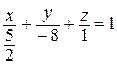 . . |
4. Можно ли пользоваться уравнениями плоскости (20)-(23) в прямоугольной декартовой системе координат и почему?
Общее уравнение плоскости
Теорема 1. Плоскость есть поверхность первого порядка, т.е. задается в аффинной системе координат уравнением первой степени 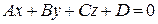 , где
, где 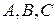 не равны нулю одновременно. Обратно, поверхность в пространстве, заданная в аффинной системе координат уравнением первой степени
не равны нулю одновременно. Обратно, поверхность в пространстве, заданная в аффинной системе координат уравнением первой степени 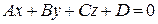 (где
(где 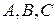 не равны нулю одновременно), есть плоскость.
не равны нулю одновременно), есть плоскость.
□ Пусть плоскость  задана точкой
задана точкой 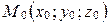 и двумя неколлинеарными векторами
и двумя неколлинеарными векторами 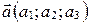 и
и 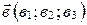 , т.е.
, т.е. 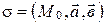 . Найдем ее уравнение.
. Найдем ее уравнение.
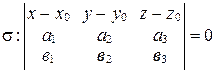 ;
; 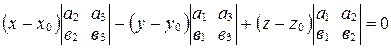 ;
;
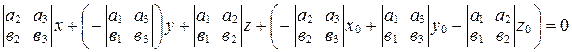 .
.
Положим 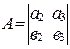 ,
, 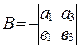 ,
, 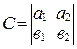 ,
, 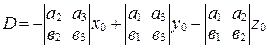 . Тогда
. Тогда 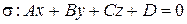 .
.
Так как векторы 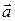 и
и 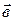 неколлинеарны, то их соответствующие координаты не пропорциональны, следовательно,
неколлинеарны, то их соответствующие координаты не пропорциональны, следовательно, 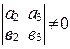 ,
, 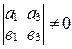 и
и 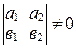 одновременно, т.е.
одновременно, т.е. 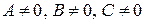 одновременно.
одновременно.
Докажем обратное утверждение. Пусть некоторая поверхность 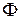 задана уравнением
задана уравнением 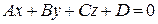 , где
, где 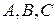 не равны нулю одновременно. Докажем, что
не равны нулю одновременно. Докажем, что 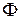 - плоскость.
- плоскость.
Пусть для определенности 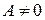 . Найдем уравнение плоскости
. Найдем уравнение плоскости 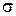 , заданной точкой
, заданной точкой 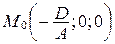 и двумя неколлинеарными векторами
и двумя неколлинеарными векторами 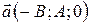 и
и 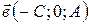 .
.
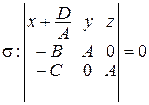 ;
;
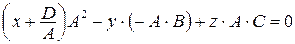 ;
; 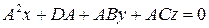 ; разделив обе части полученного уравнения на
; разделив обе части полученного уравнения на 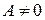 , получим:
, получим:
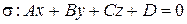 .
.
Итак, уравнение поверхности 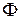 в точности совпадает с уравнением плоскости
в точности совпадает с уравнением плоскости 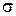 , следовательно,
, следовательно, 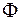 совпадает с
совпадает с 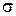 , т.е.
, т.е. 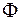 - плоскость.
- плоскость.
Если 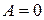 , то
, то 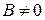 или
или 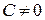 . Аналогичными рассуждениями убеждаемся, что
. Аналогичными рассуждениями убеждаемся, что 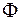 - плоскость. ■
- плоскость. ■
Уравнение 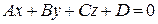 (где
(где 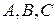 не равны нулю одновременно) называется общим уравнением плоскости. Переменные х, у, z называются текущими координатами произвольной точки плоскости.
не равны нулю одновременно) называется общим уравнением плоскости. Переменные х, у, z называются текущими координатами произвольной точки плоскости.
Задания для самостоятельной работы
1. Можно ли пользоваться общим уравнением плоскости в прямоугольной декартовой системе координат и почему?
2. Выведите в аффинной системе координат уравнение 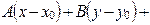
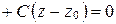 плоскости, проходящей через точку
плоскости, проходящей через точку 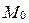 .
.
3. Дано общее уравнение плоскости 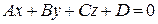 , в котором все коэффициенты при х, у и z и свободный член отличны от нуля. Получите из него уравнение плоскости «в отрезках».
, в котором все коэффициенты при х, у и z и свободный член отличны от нуля. Получите из него уравнение плоскости «в отрезках».
4. Дано параметрическое уравнение плоскости. Получите из него общее уравнение плоскости.
5. Дано общее уравнение плоскости. Получите из него параметрическое уравнение плоскости.
6. Какая поверхность в пространстве задается в аффинной системе координат уравнением: а) 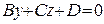 ; б)
; б) 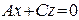 ; в)
; в) 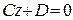 ; г)
; г) 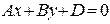 ; д)
; д) 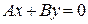 ?
?
Лемма о параллельности вектора и плоскости.
