Тема 2. отношения. функции

Отношения. Основные понятия и определения

Определение 2.1. Упорядоченной парой <x, y> называется совокупность двух элементов x и y, расположенных в определенном порядке.

Две упорядоченные пары <x, y> и <u, v> равны межу собой тогда и только тогда, когда x = u и y = v.

Пример 2.1.

<a, b>, <1, 2>, <x, 4> – упорядоченные пары.

Аналогично можно рассматривать тройки, четверки, n-ки элементов <x₁, x₂, … x_n>.

Определение 2.2. Прямым (или декартовым)произведением двух множеств A и B называется множество упорядоченных пар, таких, что первый элемент каждой пары принадлежит множеству A, а второй – множеству B:

A ´ B = {<a, b>, ç aÎ А и bÏ В}.

В общем случае прямым произведением n множеств А₁, А₂,… А_n называется множество А₁ ´ А₂ ´ …´ А_n, состоящее из упорядоченных наборов элементов <a₁, a₂, …, a_n> длины n, таких, что i- ый a_i принадлежит множеству А_i, a_i Î А_i.

Пример 2.2.

Пусть А = {1, 2}, В = {2, 3}.

Тогда A ´ B = {<1, 2>, <1, 3>,<2, 2>,<2, 3>}.

Пример 2.3.

Пусть А = {x ç0 £ x £ 1} и B = {y ç2 £ y £ 3}

Тогда A ´ B = {< x, y >, ç0 £ x £ 1и2 £ y £ 3}.

Таким образом, множество A ´ B состоит из точек, лежащих внутри и на границе прямоугольника, образованного прямыми x = 0 (ось ординат), x = 1, y = 2и y = 3.

Французский математик и философ Декарт впервые предложил координатное представление точек плоскости. Это исторически первый пример прямого произведения.

Определение 2.3. Бинарным (или двуместным)отношением r называется множество упорядоченных пар.

Если пара <x, y> принадлежит r, то это записывается следующим образом: <x, y> Î r или, что то же самое, xr y.

Пример2.4.

r = {<1, 1>, <1, 2>, <2, 3>}

Аналогично можно определить n-местное отношение как множество упорядоченных n-ок.

Так как бинарное отношение – множество, то способы задания бинарного отношения такие же, как и способы задания множества (см. разд. 1.1). Бинарное отношение может быть задано перечислением упорядоченных пар или указанием общего свойства упорядоченных пар.

Пример 2.5.

1. r = {<1, 2>, <2, 1>, <2, 3>} – отношение задано перечислением упорядоченных пар;

2. r = {<x, y> çx+ y = 7, x, y – действительные числа} – отношение задано указанием свойства x+ y = 7.

Кроме того, бинарное отношение может быть задано матрицей бинарного отношения. Пусть А = {a₁, a₂, …, a_n} – конечное множество. Матрица бинарного отношения C есть квадратная матрица порядка n, элементы которой c_ij определяются следующим образом:

c_ij =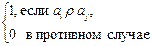

Пример 2.6.

А = {1, 2, 3, 4}. Зададим бинарное отношение r тремя перечисленными способами.

1. r = {<1, 2>, <1, 3>, <1, 4>, <2, 3>, <2, 4>, <3, 4>} – отношение задано перечислением всех упорядоченных пар.

2. r = {< a_i, a_j> ça_i < a_j; a_i, a_j Î А} – отношение задано указанием свойства "меньше" на множестве А .

3. 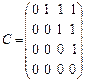– отношение задано матрицей бинарного отношения C.

Пример 2.7.

Рассмотрим некоторые бинарные отношения.

1. Отношения на множестве натуральных чисел.

а) отношение £ выполняется для пар <1, 2>, <5, 5>, но не выполняется для пары <4, 3>;

б) отношение "иметь общий делитель, отличный от единицы" выполняется для пар <3, 6>, <7, 42>, <21, 15>, но не выполняется для пары <3, 28>.

2. Отношения на множестве точек действительной плоскости.

а) отношение "находиться на одинаковом расстоянии от точки (0, 0)" выполняется для точек (3, 4) и (–2, Ö21), но не выполняется для точек (1, 2) и (5, 3);

б) отношение "быть симметричным относительно оси OY" выполняется для всех точек (x, y) и (–x, –y).

3. Отношения на множестве людей.

а) отношение "жить в одном городе";

б) отношение "учиться в одной группе";

в) отношение "быть старше".

Определение 2.4.Областью определения бинарного отношения r называется множество D_r = {x çсуществует y, что xr y}.

Определение 2.5.Областью значений бинарного отношения r называется множество R_r = {y çсуществует x, что xr y}.

Определение 2.6.Областью задания бинарного отношения r называется множество M_r = D_r ÈR_r.

Используя понятие прямого произведения, можно записать:

r Î D_r ´ R_r

Если D_r = R_r = A, то говорят, что бинарное отношение r задано на множестве A.

Пример 2.8.

Пусть r = {<1, 3>, <3, 3>, <4, 2>}.

Тогда D_r = {1, 3, 4}, R_r = {3, 2}, M_r = {1, 2, 3, 4}.