Локальная и интегральная теоремы Муавра-Лапаса
Если количество независимых испытаний достаточно большое применения формулы Бернулли становится трудоемким. Для упрощения вычислений применяют локальную и интегральную теоремы Лапласа, которые дают близкий к формуле Бернулли результат при большом количестве испытаний и не требуют больших вычислений.
ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА
Вероятность того, что в 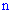 независимых испытаниях с вероятностью появления события
независимых испытаниях с вероятностью появления события 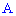 равной
равной 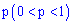 событие
событие 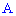 наступит ровно
наступит ровно 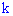 раз (безразлично в какой последовательности) определяется по приближенной формуле
раз (безразлично в какой последовательности) определяется по приближенной формуле
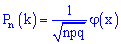
где
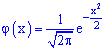 – Функция Гаусса,
– Функция Гаусса,
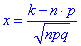 – аргумент функции Гаусса;
– аргумент функции Гаусса;
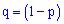 – вероятность противоположного события
– вероятность противоположного события  .
.
Формулу 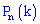 называют локальной формулой Лапласа.
называют локальной формулой Лапласа.
Функция 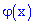 обладает следующими свойствами:
обладает следующими свойствами:
1) она является четной функцией 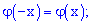 ;
;
2) для значений аргумента больше четырех она сколь угодно мала 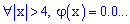
Теорему Лапласа рекомендуется применять при значениях произведения больше девяти
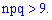
ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА
Вероятность, что в 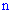 независимых испытаниях событие
независимых испытаниях событие 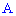 с вероятностью появления
с вероятностью появления 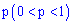 наступит не менее
наступит не менее 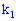 раз и не более
раз и не более 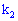 (независимо от последовательности появления) приближенно определяется зависимостью
(независимо от последовательности появления) приближенно определяется зависимостью
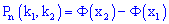
где 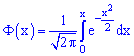 – интегральная функция Лапласа;
– интегральная функция Лапласа;
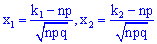 – аргументы интегральной функции распределения;
– аргументы интегральной функции распределения;
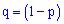 – вероятность невыполнения события
– вероятность невыполнения события 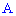 .
.
Функция 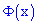 обладает следующими свойствами:
обладает следующими свойствами:
1) она является нечетной функцией
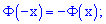
2) для аргументов больше пяти она равна 0,5
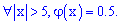
Значение обеих функций 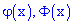 находят из таблиц в которых функции с достаточной точностью протабульовани.
находят из таблиц в которых функции с достаточной точностью протабульовани.
--------------------------------
Рассмотрим задачи на применение каждой из теорем.
Пример 1. Есть 100 лунок по которым случайным образом разбрасывают 30 шариков. Каждый шарик с равной вероятностью может попасть в любую лунку (в одну лунку попадает не более одного шарика). Найти вероятность того, что в выбранную лунку попадет ровно один шарик.
Решение. Проводится 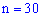 независимых бросков шариков с одинаковой вероятностью попадания при каждом броске
независимых бросков шариков с одинаковой вероятностью попадания при каждом броске
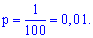
Вероятность попадания в лунку ровно одного шарика определим по локальной формулой Лапласа:
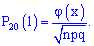
Для этого определяем составляющие
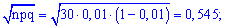
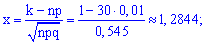
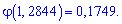
и подставим в зависимость
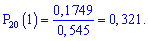
--------------------------------
Пример 2. Проводится 200 независимых опытов с вероятностью успеха в каждом 24%. Какова вероятность успешного проведения 50 опытов?
Решение. По условию 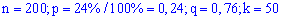
находим составляющие формулы Лапласа
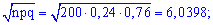
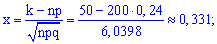
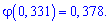
Подставляя в формулу, находим
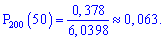
--------------------------------
Пример 3. Вероятность выхода из строя за смену одного станка равна 0,1. Определить вероятность выхода из строя от 2 до 13 станков при наличии 100 станков.
Решение. Записываем входные данные
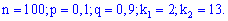
Для подобных примеров применяем интегральную формулу Муавра-Лапласа и находим вероятность
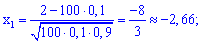
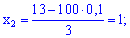
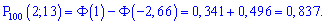
--------------------------------
Решение задач по приведенным теоремам позволяет при большом количестве испытаний находить приближенное значение вероятности. Локальная теорема необходима при определении конкретного количества появления событий, интегральная теорема Муавра-Лапласа - в случаях, когда задан диапазон возможного количества появлений события.
