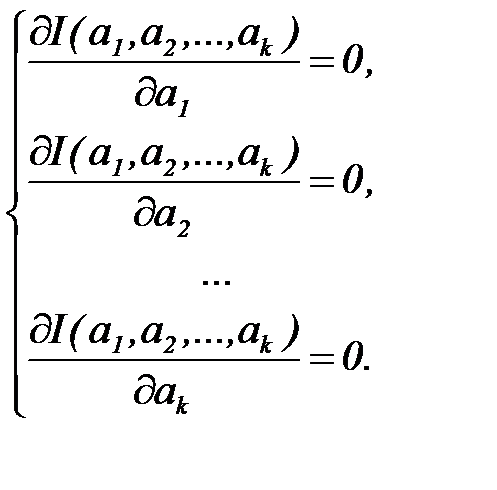Метод наименьших квадратов. Для получения неизвестных оценок параметров распределения генеральной совокупности Х определенное количество выборочных начальных и/или центральных моментов

Метод моментов

Для получения неизвестных оценок параметров 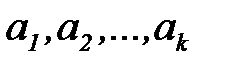распределения генеральной совокупности Х определенное количество выборочных начальных и/или центральных моментов приравниваются к соответствующим теоретическим аналогам, полученным для предполагаемого теоретического закона распределения.

Предположим, что 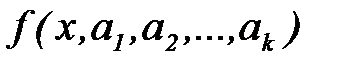- плотность распределения случайной величины Х. Определим с помощью этой плотности k каких-либо моментов случайной величины, например, первые k начальных моментовпо формулам

.

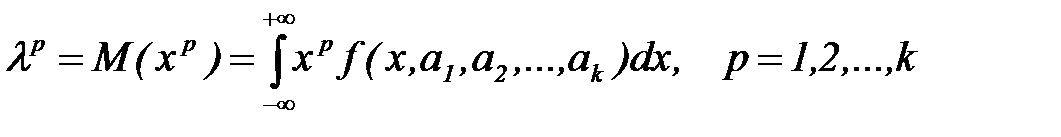По выборке наблюдений случайной величины найдем значения соответствующих выборочных моментов

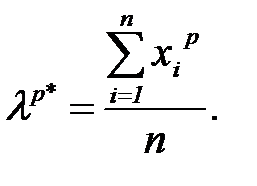
Попарно приравнивая теоретические моменты их выборочным аналогам, получаем систему из kуравнений с k неизвестными, разрешая которую получаем искомые значения.

Согласно методу моментов, параметры 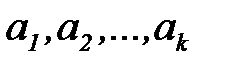выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим статистическим характеристикам. Например, если теоретическая кривая 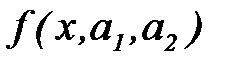зависит только от двух параметров 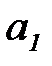и 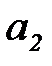, эти параметры выбираются так, чтобы математическое ожидание 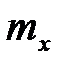и дисперсия 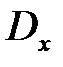теоретического распределения совпадали с соответствующими статистическими характеристикам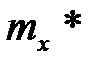и и 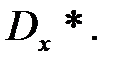Если кривая 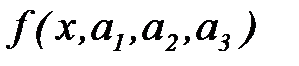зависит от трех параметров, можно подобрать их так, чтобы совпали первые три момента и т.д. При выравнивании статистических рядов может оказаться полезной специально разработанная система кривых Пирсона, каждая из которых зависит в общем случае от четырех параметров. При выравнивании эти параметры выбираются с тем расчетом, чтобы сохранить первые четыре момента статистического распределения (математическое ожидание, дисперсию, третий и четвертый моменты). Следует заметить, что при выравнивании статистических рядов нерационально пользоваться моментами порядка выше четвертого, так как точность вычисления моментов резко падает с увеличением их порядка.

Метод наименьших квадратов

При сглаживании эмпирических зависимостей очень часто исходят из так называемого принципа или метода наименьших квадратов, считая, что наилучшим приближением к эмпирической зависимости в данном классе функций является такое, при котором сумма квадратов отклонений обращается в минимум. При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений, а из соображения, связанных с физикой решаемой задачи, с учетом характера полученной эмпирической кривой и степени точности произведенных наблюдений. Часто принципиальный характер функции, выражающей исследуемую зависимость, известен заранее из теоретических соображении, из опыта же требуется получить лишь некоторые численные параметры, входящие в выражение функции; именно эти параметры подбираются с помощью метода наименьших квадратов.

Задача восстановления некоторой функции 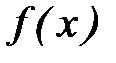методом наименьших квадратов требует, чтобы мера отклонения экспериментальных значений от выбранной функции была минимальной в заданных 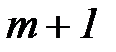точках 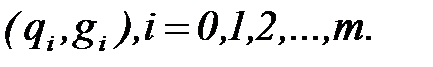В качестве таких пар точек, как правило, выбирают середины интервалов гистограммы и высоты, им соответствующие. Затем строится функция расхождений теоретических и эмпирических значений в точках 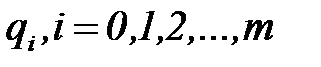, которая подлежит минимизации

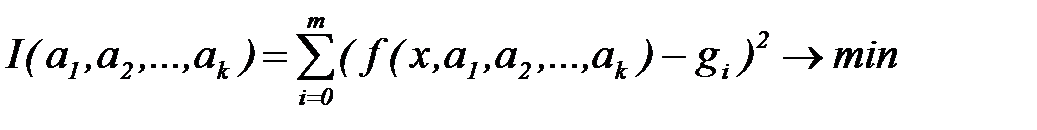
Требуется подобрать коэффициенты 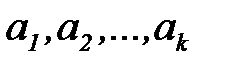так, чтобы величина Iбыла наименьшей. Для решения этой задачи находят частные производные от функции 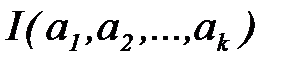по всем переменным 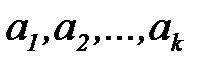, приравнивают их к нулю и решают полученную систему уравнений