Сложение вращений твёрдого тела.

В этом параграфе будут рассмотрены движение тела относительно параллельных, пересекающихся осей.

1. Сложение вращений относительно параллельных осей.

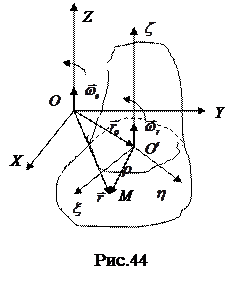Предположим, что твердое тело вращается вокруг некоторой оси, которая в свою очередь вращается вокруг другой, неподвижной оси, ей параллельной. Зная угловую скорость вращения тела вокруг подвижной оси и угловую скорость вращения самой оси вокруг неподвижной оси, определим абсолютное движение тела. Относительным движением в данном случае является вращение твердого тела вокруг оси по отношению к системе координат в свою очередь вращающейся вокруг оси Oz неподвижной (абсолютной) системы координат Oxyz; вектор угловой скорости вращения тела вокруг оси ', направленный вдоль этой оси, обозначим 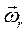и назовем относительной угловой ско­ростью. Вращение самой системы координат 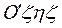по отношению к системе Oxyz будет переносным движением; вектор угловой скорости этого вращения, направленный по оси Oz, обозначим 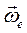и назовем переносной угловой скоростью. Заметим прежде всего, что из условия параллельности векторов 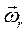и 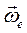все точки тела как в относительном, так и в переносном движении остаются в плоскостях, перпендикулярных к этим векторам, следовательно, абсо­лютное движение тела будет пло­ским. Точка М этой плоской фигуры, имеющая вектор-радиус по отношению к О' и вектор-радиус 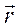по отношению к О, будет двигаться с абсолютной скоростью 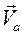, равной

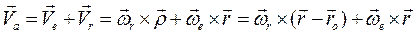
или 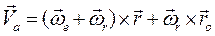(2.41)

С другой стороны, рассматриваемое плоское движение можно представить как мгновенное вращение около оси, проходящей через мгновенный центр и перпендикулярной к плоскости движения. Чтобы найти положение этой оси, обозначим вектор-радиус мгно­венного центра Р через 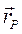и напишем условие, что абсолютная скорость точки плоской фигуры Р равна нулю. Полагая в равенстве (2.41) 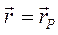и 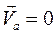получим

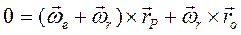(2.42)

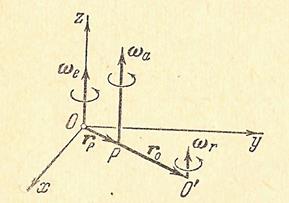Рис.45.

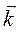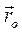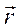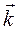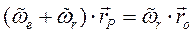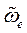Умножим обе части этого равенства векторно на единичный вектор оси Oz; тогда, раскрывая двойное векторное произведение и так как вектора и перепендикулярны единичному вектору , получим: , где и 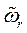согласно принятым обозначениям представляют алге­браические величины угловых скоростей (знак плюс, если вращение положительно для наблюдателя, смотрящего с оси Oz или знак минус в противоположном случае). Итак, при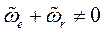

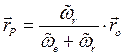(2.43)

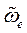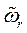Из последнего равенства видно, что при любых зависимостях между и мгновенный центр Р находится на линии 00' .Чтобы найти угловую скорость вращения вокруг мгновенного центра, вычтем (2.42) из (2.41); получим:

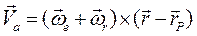
Это — формула вращательной скорости вокруг точки Р, с абсолютной угловой скоростью, равной

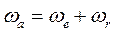Итак, рассматриваемое абсолютное движение твердого тела эквивалентно вращению вокруг мгновенной оси, проходящей через мгновенный центр Р, с абсолютной угловой скоростью, равной геометрической сумме переносной и относительной угло­вых скоростей. Отметим возможные случаи расположе­ния мгновенной оси.

1. Направление вращений одинаково, т. е. 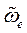и 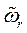имеют один и тот

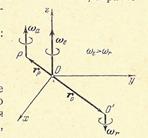Рис.46.

же знак, например положительный. В этом случае из уравнений (2.43) видно, что точка лежит между центрами О и 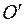на расстояниях, обратно пропорциональных величинам угловых скоростей (рис 46). Абсолютная угловая скорость вращения вокруг оси, проходящей через точку Р, по (63) равна сумме угловых скоростей.

2. Направление вращений различно, т. е. 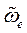и 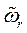имеют раз­личные знаки, например 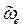> 0, a 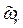< 0, причем положим для определенности, что 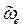> 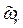. В этом случае из формулы (62) сле­дует: 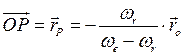.Точка Р, следовательно, лежит за точкой О.

В качестве приложения рассмотрим вопрос об определении угловых скоростей в эпициклическом зацеплении зубчатых колес (рис.47).Обычно эпициклическим или планетарным механизмом называют сцепление двух или нескольких колес, из которых одно вращается около неподвижной оси, другие — около осей, закрепленных на подвижной рукоятке, причем зацепление может быть как внешним, так и внутренним. Колеса, соединенные с вращаю­щейся рукояткой, называют сателлитами.

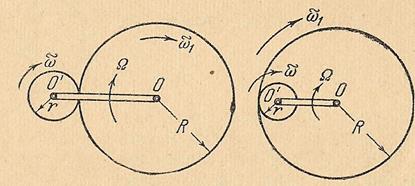Рис. 47.

Выведем общее соотношение между угловыми скоростями колес и рукоятки по отношению к основанию механизма в случаях внешнего и внутреннего зацепления. На рисунке все угловые скорости показаны в направлении по часовой стрелке; знак в дальнейшем покажет истинное направление вращений. Угловая скорость рукоятки обозначена через 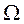.Придадим механизму в целом вращение с угловой скоростью (- 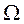), равной по величине угловой скорости рукоятки, но противо­положной ей по направлению. Тогда по теореме о сложении угловых скоростей основание механизма станет подвижным звеном, имеющим угловую скорость (- 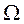), а рукоятка, наоборот, станет неподвижной и будет играть роль основания механизма. Механизм с перемещаю­щимися осями превратится при этом в систему зубчатых колес с неподвижными осями, но угловые скорости колес будут уже равны соответственно 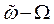и 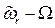. Тогда, пользуясь известным соотношением между угловыми ско­ростями и радиусами, найдем:

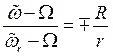здесь знак "-“ для внешнего зацепления и “+“ для внутреннего.

3. Направления вращений различны, но угловые скорости их равны по величине ( 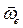=- 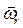).Этот случай представляет некоторую особенность, так как векторы 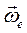и 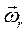образуют пару векторов. В этом случае имеет место мгновенно-поступательное движение тела.

Объединяя все три случая, приходим к следующему результату: при сложении вращений вокруг параллельных осей уг­ловые скорости складываются так же, как параллельные силы в статике. При проведении этой аналогии переносная и относительная угло­вые скорости рассматриваются как слагаемые силы, а абсолютная угловая скорость соответствует равнодействующей силе.

2. Теорема о сложении вращений вокруг пересекающихся осей.

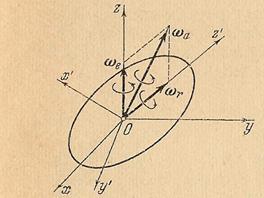Рис.48.

Пусть относительное вращение тела с относительной угловой скоростью 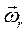происходит вокруг оси Oz' , а переносным движением является вращение системы Ox'y'z' с переносной угловой скоростью 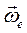вокруг неподвижной оси Oz, пересе­кающейся с осью Oz' в точке О. Абсо­лютным движением будет движение тела по отношению к системе координат Oxyz. Рассматриваемое абсолютное дви­жение тела является вращением вокруг неподвижного центра О. Всякое вращение тела вокруг не­подвижного центра можно представить как вращение вокруг некоторой мгно­венной оси. Определим направление мгно­венной оси и найдем вектор абсолютной угловой скорости враще­ния тела. Для этого возьмем какую-нибудь точку М тела с вектор-радиусом 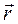и напишем по теореме о сложении скоростей: в данном случае

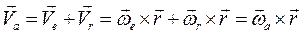
откуда следует, что 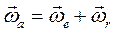т.е. абсолютная угловая скорость при вращении тела относительно пересекающихся осей равна геометрической сумме относительной и переносной угловых скоростей. В качестве иллюстрации рассмотрим случай регулярной прецессии твёрдого тела, когда

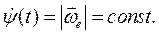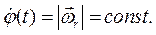, и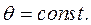

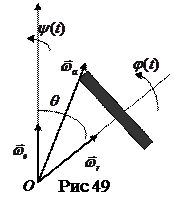при этом 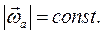Тогда угловое ускорение тела будет равно (по формуле 2.25)

,

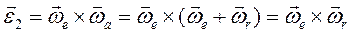и 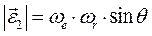. При решении этой задачи методом сложения вращений надо рассмотреть отдельно два вращения тела относительно двух неподвижных осей. Первое вращение – это « стоп переносное движение - =0» и рассматривается задача о вращении тела относительно подвижной оси по закону , тогда:

.

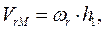
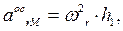
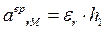В нашем случае последнее слагаемое равно нулю, - кратчайшее расстояние от точки до оси относительного вращения.

Второе вращение – это « стоп относительное движение - 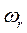=0» и рассматривается задача о вращении тела относительно неподвижной оси по закону 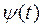. Будем иметь:

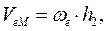
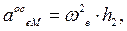
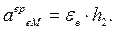
И в этом случае последнее слагаемое равно нулю, 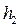- кратчайшее расстояние от точки до оси переносного вращения. Третья составляющая ускорения – ускорение Кориолиса, равное

.

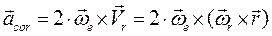Величина этого ускорения равна 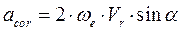. Чтобы получить величину абсолютного ускорения, необходимо выбрать оси координат и спроектировать все ускорения на выбранные оси. Получив 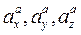, получим .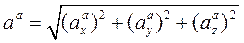