Практична робота №6 Тема: Методи мінімізації функції.

МетаОзнайомитися з методами мінімізації (максимізації) функції декількох змінних.

Теоретичні відомості

Необхідні умови точки локального мінімуму:

, .

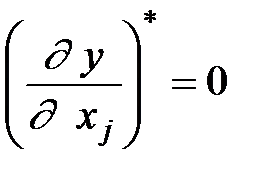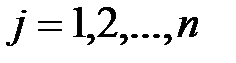У матричному вигляді необхідні умови точки локального мінімуму запишуться в наступному вигляді:

,

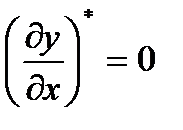де 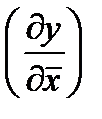= 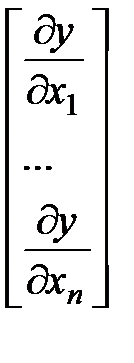- градієнт функції.

Таким чином, в точці локального мінімуму градієнт функції дорівнює нулю.

Точка, для якої виконується рівність 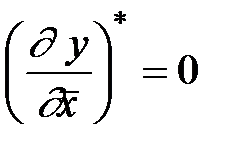називається стаціонарною точкою функції .

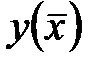Геометрично ця умова означає, що гіперплощина, дотична до функції в точці оптимуму, паралельна гіперплощині визначення цієї функції. Так, для функції однієї змінної це – дотична лінія, паралельна осі х; для функції два змінних – плоскість, паралельна плоскості х1 і х2 .

На рис. 1 приведені різні приклади стаціонарних точок для функції однієї змінної. Стаціонарна точка не обов'язково має бути екстремальною. Прикладом такої крапки може служити точка перегину функції.

Рис. 1. Приклади стаціонарних точок функції однієї змінної

На мал. 2 приведена функція двох змінних

.

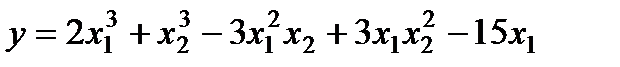Функція зображена у вигляді еквіпотенціальних кривих на координатній плоскості Як видно з малюнка, функція має чотири стаціонарні точки, в кожній з яких її приватні похідні дорівнюють нулю, тобто виконується необхідна умова локального екстремуму. При цьому одна стаціонарна точка, розташована в першому квадранті, відповідає точці локального мінімуму функції. Інша, симетрична першою і розташована в третьому квадранті, відповідає точці локального максимуму функції. Дві стаціонарні точки, що залишилися, розташованими в другому і четвертому квадрантах і симетричні між собою.

1,5

-1,5

у = - 3

у = 9

у = 6

у = 3

у = 0

х1

у = 3

--3

у = - 18

у = - 12

у = - 6

у = 6

у = 0

у = - 3

у = - 6

у = - 9

у = 12

у = 18

у = - 6

-3

-2

-1

Рис. 2. Еквіпотенціальні криві і стаціонарні точки функції двох змінних

Рівність нулю градієнта функції – це необхідна, але недостатня умова для існування локального екстремуму.

Визначимо достатні умови для точки локального мінімуму.

Екстремальна точка завжди є стаціонарною.

Розкладемо функцію в околиці стаціонарної точки в ряд Тейлора, обмежуючись квадратичними членами розкладання:

,

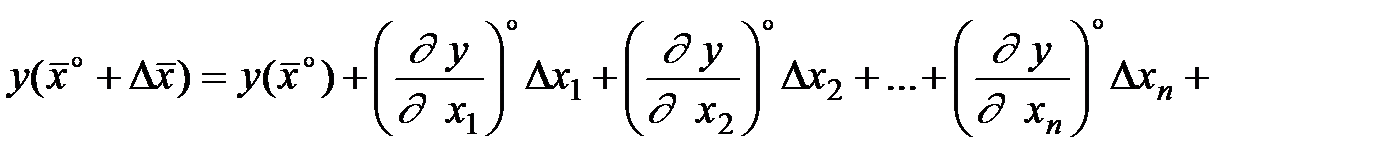
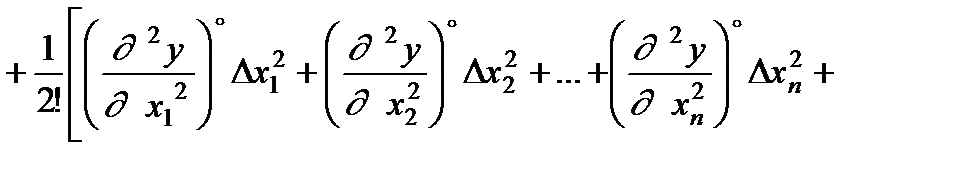
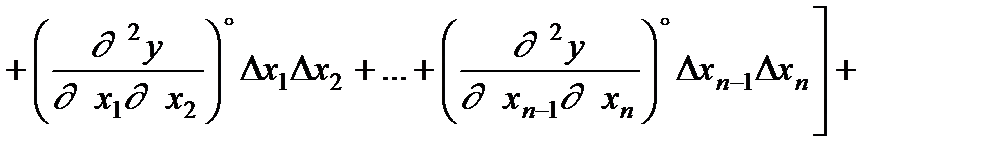
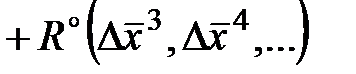де R - частина ряду розкладання, яка залежить від приросту вектора змінних третього і більшого порядку; індекс « 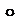» при похідних є ознака їх обчислення в стаціонарній крапці .

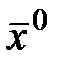Дане співвідношення можна записати в наступному вигляді:

.

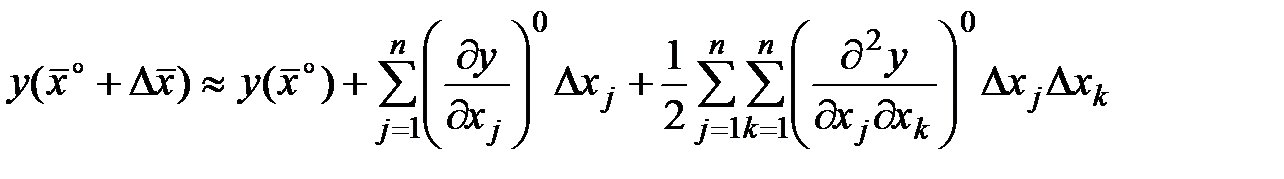Перепишемо вираз в матричному вигляді:

,

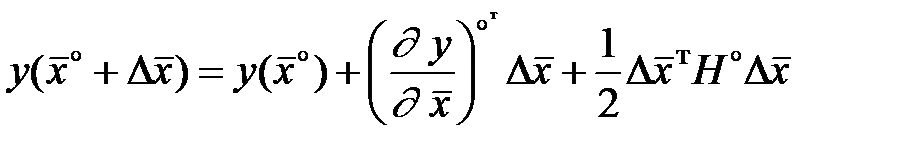де Н- матриця Гесса (симетрична матриця порядку 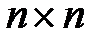елементами якої є другі похідні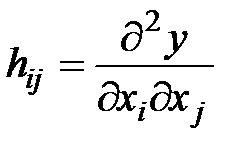

;
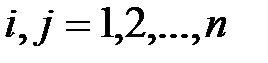
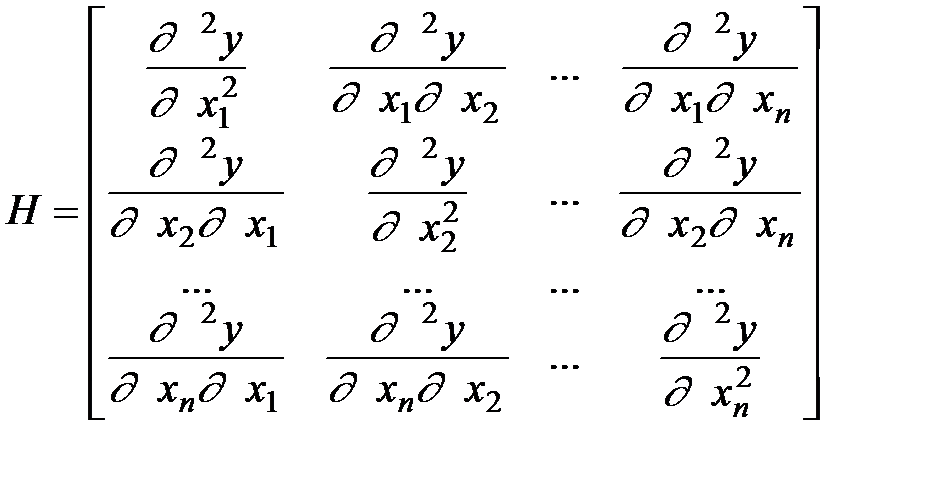