Элементы теории вероятностей
Основные характеристики и экспериментальный анализ случайных величин
Цель работы: изучение основных понятий теории вероятностей, ознакомление с основными характеристиками случайных величин и возможными способами их экспериментального определения
ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ
Элементы теории вероятностей
Интегральная функция распределения F(x) случайной величины Х показывает вероятность того, что случайная величина не превышает некоторого заданного или текущего значения x, т.е. F(x) = Р{Х £ х}. Следовательно, вероятность того, что значение случайной величины Х заключено между х1 и х2, равна разности значений функции распределения, вычисленных в этих двух точках:
P{x1 < X £ x2}= F(x2) – F(x1). (1.2)
Аналогично
P{X > x} = 1 – F(x). (1.3)
Интегральная функция распределения случайной величины Х обладает следующими свойствами:
1) lim F(x) = F(- ¥) = 0;
2) lim F(x) = F(¥) = 1;
3) F(x) ³ 0;
4) F(x2) ³ F(x1), если x2 > x1.
| F(х) |
| x |
| Рис. 1.1 |
Если функция F(x) дифференцируема для всех значений случайной величины Х, то закон распределения вероятностей и может быть выражен в аналитической форме также с помощью дифференциальной функции распределения вероятностей:
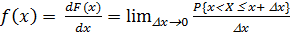 (Dx > 0). (1.4)
(Dx > 0). (1.4)
Таким образом, значение функции 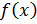 приближенно равно отношению вероятности попадания случайной величины в интервал
приближенно равно отношению вероятности попадания случайной величины в интервал 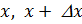 к длине
к длине 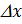 этого интервала, когда
этого интервала, когда 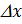 – бесконечно малая величина. Поэтому функцию
– бесконечно малая величина. Поэтому функцию 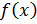 называют также функцией плотности распределения вероятностей (или короче – функцией плотности вероятности).
называют также функцией плотности распределения вероятностей (или короче – функцией плотности вероятности).
Отметим основные свойства функции 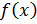 :
:
1) f(x)³ 0;
2) 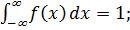
3) 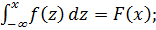
4) 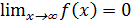 (z – переменная интегрированная).
(z – переменная интегрированная).
С помощью дифференциальной функции распределения вычисляется вероятность нахождения случайной величины в любой области из множества ее возможных значений. В частности,
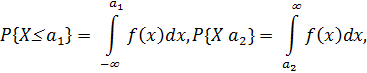
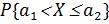 =
= 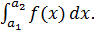 (1.5)
(1.5)
Для непрерывной случайной величины вероятность можно определить как относительную долю площади под кривой плотности распределения вероятностей 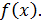 Так, например, вероятность того, что случайная величина Х примет значение, меньшее а1, равна относительной доле площади под кривой
Так, например, вероятность того, что случайная величина Х примет значение, меньшее а1, равна относительной доле площади под кривой 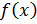 слева от точки а1 (рис. 1.2, а); вероятность того, что эта величина Х примет значение, большее а2, равна относительной доле площади под кривой
слева от точки а1 (рис. 1.2, а); вероятность того, что эта величина Х примет значение, большее а2, равна относительной доле площади под кривой 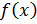 справа от точки а2 (рис. 1.2, б); вероятность того, что она примет значение, заключенное между а1 и а2, равна относительной доле площади под кривой
справа от точки а2 (рис. 1.2, б); вероятность того, что она примет значение, заключенное между а1 и а2, равна относительной доле площади под кривой 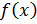 между точками а1 и а2 (рис. 1.2, в).
между точками а1 и а2 (рис. 1.2, в).
Как интегральная, так и дифференциальная функции распределения являются исчерпывающими вероятностными характеристиками случайной величины. Однако некоторые свойства случайных величин могут быть описаны более просто с помощью определенных числовых параметров. Наибольшую роль среди них на практике играют два параметра, характеризующие центр рассеяния (центр распределения) случайной величины и степень ее рассеяния вокруг этого центра. Наиболее
| f(x))x) |
| x |
| f(x))x) |
| x |
| f(x))x) |
| x |
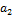 |
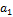 |

Рис. 1.2
а) б) в)
распространенной характеристикой центра распределения является математическое ожидание mx случайной величины Х (часто называемое также генеральным средним значением):
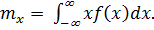 (1.6)
(1.6)
Степень рассеяния случайной величины Х относительно mx может быть охарактеризована с помощью генеральной дисперсии 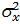 :
:
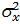 =
= 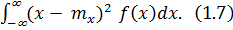
Если 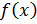 все в большей степени концентрируется вблизи mx, то значения
все в большей степени концентрируется вблизи mx, то значения 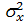 уменьшаются. Если же имеются весьма удаленные от mx значения случайной величины Х и для них
уменьшаются. Если же имеются весьма удаленные от mx значения случайной величины Х и для них 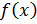 не слишком мала, то дисперсия
не слишком мала, то дисперсия 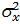 увеличивается. Квадратный корень из дисперсии
увеличивается. Квадратный корень из дисперсии 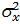 называется средним квадратическим отклонением sx.
называется средним квадратическим отклонением sx.
Зачастую для описания практической ситуации оказывается необходимым использования одновременно нескольких (в простейшем случае – двух) случайных величин. Для задания вероятностных свойств двух случайных величин X, Y используются двумерные (совместные) функции распределения вероятностей: интегральная F(x, y) и дифференциальная f(x, y). Функция F(x, y), характеризуется вероятностью того, что первая случайная величина принимает некоторое значение, меньшее или равное x, а вторая – значение меньшее или равное y, называется интегральной функцией совместного распределения двух случайных величин:
F(x,y) = P{X £ x; Y£ y}. (1.8)
Как и для одной непрерывной случайной величины, если функция F(x,y) достаточно гладкая, то ее можно продифференцировать, в результате чего получится двумерная дифференциальная функция распределения вероятностей (двумерная плотность вероятностей):
f(x, y)= 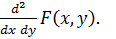 (1.9)
(1.9)
Функция f(x, y) обладает следующими свойствами:
1) f(x, y)³ 0;
2) 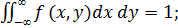
3) 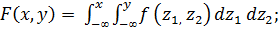
4) 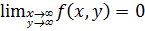 (z1 и z2 – переменные интегрированная).
(z1 и z2 – переменные интегрированная).
Вероятность того, что случайные величины X, Y одновременно попадут в некоторую произвольную область W, составляет
P{(X,Y)Î W} = 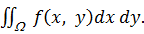 (1.10)
(1.10)
В частности,
P{a1 < X £ a2; b1 < Y £ b2} = 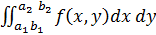 .(1.11)
.(1.11)
По известной двумерной плотности f(x, y) легко найти частные (одномерные) функции распределения f(x), f(y) каждой случайной величины:
f(x) = 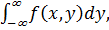 f(y) =
f(y) = 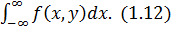
Две случайные величины X и Y называются независимыми, если
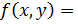 f(x) f(y). (1.13)
f(x) f(y). (1.13)
Как и в одномерном случае, основные свойства двумерной совокупности величин X и Y могут быть охарактеризованы с помощью ряда цифровых параметров. При этом в качестве наиболее употребительных параметров, описывающих поведение каждой из случайных величин в отдельности, как и выше, используются математическое ожидание и дисперсия соответствующей случайной величины mx, my, 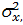
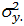 Кроме подобного рода параметров для двумерной совокупности могут быть построены параметры, характеризующие степень взаимозаменяемости переменных X и Y. Простейшими из них являются ковариация двух случайных величин (называемая также корреляционным моментом).
Кроме подобного рода параметров для двумерной совокупности могут быть построены параметры, характеризующие степень взаимозаменяемости переменных X и Y. Простейшими из них являются ковариация двух случайных величин (называемая также корреляционным моментом).
cov(X, Y) = 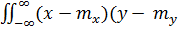 ) f(x,y) dx dy, (1.14)
) f(x,y) dx dy, (1.14)
а также нормированный показатель связи – коэффициент корреляции
rxy = 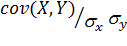 . (1.15)
. (1.15)
По своему физическому смыслу коэффициент корреляции является далеко не исчерпывающей характеристикой статистической связи, характеризующая лишь степень линейной зависимости между X и Y. Коэффициент корреляции меняется в пределах -1 £ rxy £ 1. Если rxy = 1, то случайные величины полностью положительно коррелированы, т.е. y = a0 + a1 x, где a0, a1 – постоянные, причем a1 > 0. Если же rxy = -1, то случайные величины полностью отрицательно коррелированы, т.е. y = a0 - a1. Если rxy = 0, то говорят, что случайные величины X и Y не коррелированы: a1 = 0. В том случае, когда X и Y – независимые случайные величины, для них rxy = 0; следовательно, они и не коррелированы. Обратное утверждение в общем случае не верно: X и Y могут быть связаны даже функционально и все же иметь нулевой коэффициент корреляции (при этом, конечно, функциональная связь должна быть нелинейной).
Все описанные выше функции и связанные с ними параметры являются теоретическими, характеризующими определенные свойства изучаемого объекта. На практике почти всегда эти характеристики независимы и возникает задача экспериментального (эмпирического) определения тех или иных характеристик случайных величин на основе наблюдений.
