Теоретические сведения
СОДЕРЖАНИЕ
1. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ 5
1.1. Теоретические сведения. 5
1.2. Примеры выполнения заданий. 8
2. РЕШЕНИЕ ЗАДАЧ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ.. 15
2.1. Теоретические сведения. 14
2.2. Задачи, описывающие движение. 14
2.3. Задачи, описывающие работу. 22
2.4. Задачи, описывающие смешивание веществ. 26
2.5. Задачи на проценты.. 29
2.6. Задачи на состав числа. 33
2.7. Разные задачи. 39
2.8. Задачи для самостоятельного решения. 45
3. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ЗНАК АБСОЛЮТНОЙ ВЕЛИЧИНЫ 49
3.1. Теоретические сведения и примеры.. 49
4. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ 59
4.1. Показательные уравнения. 59
4.2. Логарифмические уравнения. 64
5. ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА И
УРАВНЕНИЯ.. 73
5.1. Теоретические сведения и примеры.. 73
5.2. Задачи для самостоятельного решения. 81
6. НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ 83
6.1. Теоретические сведения и примеры.. 83
6.2. Задачи для самостоятельного решения. 89
7. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ 90
7.1. Иррациональные уравнения. 90
7.2. Иррациональные неравенства. 101
7.3. Задачи для самостоятельного решения. 112
8. ПОСТРОЕНИЕ ОБЛАСТИ РЕШЕНИЯ СИСТЕМЫ НЕРАВЕНСТВ НА ПЛОСКОСТИ В ДЕКАРТОВЫХ КООРДИНАТАХ.. 102
8.1. Теоретические сведения и примеры.. 102
8.2. Задачи для самостоятельного решения. 118
9. ПОСЛЕДОВАТЕЛЬНОСТИ И ПРОГРЕССИИ.. 120
9.1. Теоретические сведения и примеры.. 120
9.2. Задачи для самостоятельного решения. 126
10. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ.. 128
10.1. Теоретические сведения. 128
10.2. Примеры решения задач. 134
11. РЕШЕНИЕ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.. 142
11.1. Теоретические сведения и примеры.. 142
11.2. Задания для самостоятельного решения. 150
12. ВАРИАНТЫ ПИСЬМЕННОГО ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО МАТЕМАТИКЕ 152
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Теоретические сведения
Алгебраическим выражением называется выражение, в котором числа и буквы соединены действиями сложения, вычитания, умножения, деления, возведения в степень или извлечения арифметического корня. Равенство, обе части которого принимают одинаковые числовые значения при любых допустимых значениях входящих в него букв, называется тождеством. При выполнении тождественных преобразований алгебраических выражений нужно знать порядок выполнения действий, правила действий с дробями и степенными выражениями, формулы сокращенного умножения.
Порядок выполнения действий:
1) действия с одночленами;
2) действия в скобках;
3) умножение или деление (в порядке появления);
4) сложение или вычитание (в порядке появления).
Обыкновенная дробь – число вида 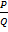 где p целое число,
где p целое число, 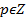 ;
;
q – натуральное число, 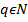 .
.
Две дроби равны:  =
= 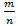 если
если 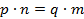
Основное свойство дробей: 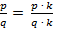 где
где 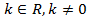
Действия с дробями:
1) сложение: 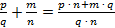 ;
;
2) вычитание: 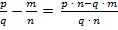 ;
;
3) умножение: 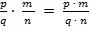 ;
;
4) деление: 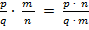
Целое число можно представить в виде дроби со знаменателем, равным единице: 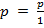
Положительная дробь  называется правильной, если
называется правильной, если 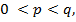 и неправильной, если
и неправильной, если 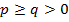 .
.
Если  неправильная дробь, то ее можно представить в виде
неправильная дробь, то ее можно представить в виде 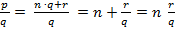 смешанная дробь,
смешанная дробь, 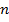 – целая часть,
– целая часть,  – дробная часть.
– дробная часть.
Дробь  , где
, где 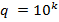 , называется десятичной. Десятичная дробь записывается в виде выражения, в котором целая и дробная части отделены запятой, например,
, называется десятичной. Десятичная дробь записывается в виде выражения, в котором целая и дробная части отделены запятой, например, 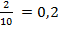 ;
; 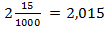 .
.
Основные свойства степени с действительным показателем:
1) 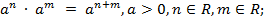
2) 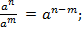
3) 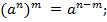
4) 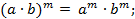
5) 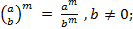
6) 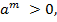 если a
если a 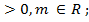
7) 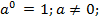
8) 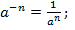
9) 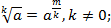
10) если 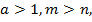 то
то 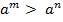
11) если 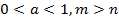 то
то 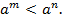
Формулы сокращенного умножения:
1) разность квадратов 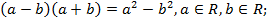
2) квадрат суммы двух чисел 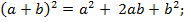
3) квадрат разности двух чисел 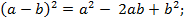
4) куб суммы двух чисел 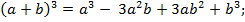
5) куб разности двух чисел 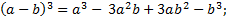
6) сумма кубов двух чисел 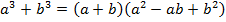 ;
;
7) разность кубов двух чисел 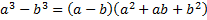 .
.
При доказательстве тождеств полезно также помнить правило разложения на множители квадратного трехчлена. Пусть 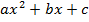 – квадратный трехчлен,
– квадратный трехчлен, 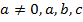 – действительные числа.
– действительные числа.
Если 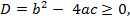 то квадратный трехчлен имеет действительные корни:
то квадратный трехчлен имеет действительные корни:
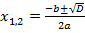 тогда
тогда 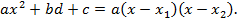
Если 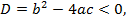 то квадратный трехчлен не имеет действительных корней, т. е. выражение
то квадратный трехчлен не имеет действительных корней, т. е. выражение 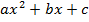 либо строго больше нуля, либо строго меньше нуля. Знак квадратного трехчлена в этих случаях совпадает со знаком множителя a, т. е.
либо строго больше нуля, либо строго меньше нуля. Знак квадратного трехчлена в этих случаях совпадает со знаком множителя a, т. е. 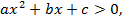 если
если 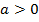 и
и 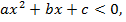 если
если 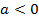 .
.
Примеры, в которых требуются преобразования алгебраических выражений, могут встретиться в самых разных разделах: при нахождении области определения функции, решении неравенств, уравнений или систем уравнений. Кроме того, в экзаменационных вариантах имеются задания, непосредственно связанные с преобразованиями. В вариантах ЕГЭ такие примеры чаще всего встречаются в части А. Ниже приведены образцы решения подобных задач.
