Подготовка к экзамену. Практика
Подготовка экзамену. Теория.
1.Что такое числовая матрица? Какие правила действия с матрицами вы знаете? Какие матрицы можно перемножать? У каких матриц существует обратная матрица? Как вычисляются определители второго и третьего порядков?
2. Какие системы уравнений называют линейными? Сколько решений может иметь система линейных уравнений? Какие бывают системы линейных уравнений? Сколько правил решения таких систем вы знаете?
3. Что такое свободный вектор и какие правила действия с векторами вы знаете? Какие векторы называют коллинеарными векторами? Как определяются координаты вектора и для чего нужны координаты векторов? Что такое проекция вектора на направление и зачем она нужна? Какие произведения векторов вы знаете? Дайте определение каждого произведения и правило его вычисления в координатах.
4. Какие кривые второго порядка вызнаете? Сформулируйте правило по которому определяется каждая кривая второго порядка. Как по заданному каноническому уравнению кривой определить: полуоси, фокусы, эксцентриситет, директрисы, асимптоты, если они для данной кривой существуют.
5. Чтобы написать уравнение прямой на плоскости, нужно задать….. Как связаны между собой уравнения параллельных (перпендикулярных) прямых на плоскости? Какие уравнения плоскостей в пространстве вы знаете? Что нужно задать, чтобы написать уравнение конкретной прямой в пространстве? Как связаны между собой : уравнения параллельных плоскостей(прямых)? уравнения перпендикулярных плоскостей (прямых)? Как зная уравнения линий найти точку их пересечения?
6. Опишите основные элементы поведения графика функции. Как определяется производная? Каков её геометрический смысл? Физический смысл? Для чего нужна таблица производных? Какие правила дифференцирования вы знаете? Как определить стационарные точки функции? Для чего нужна первая производная при исследовании функции? Сформулируйте соответствующее правило. Для чего нужна вторая производная при исследовании функции? Сформулируйте соответствующее правило. Что такое кривизна функции в точке? С помощью чего исследуется поведение функции при удалении точек её графика в бесконечность. Для чего нужно правило Лопиталя?
Подготовка к экзамену. Практика.
1.Решить системы линейных алгебраических уравнений матричным методом и методом Крамера, Гаусса.
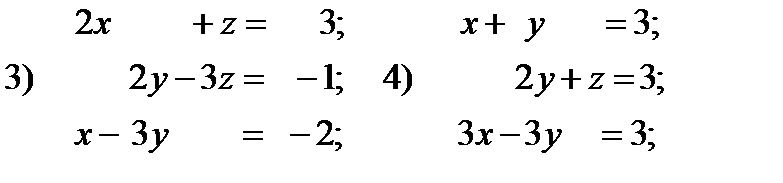
2.Написать уравнение прямой линии проходящей через точку 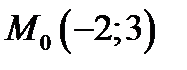 и перпендикулярно прямой линии:
и перпендикулярно прямой линии:
1) 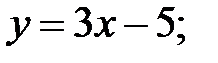 2)
2) 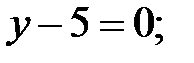 3)
3) 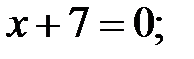 4)
4) 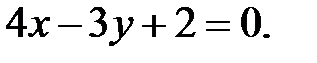
3. Найти острый угол между прямыми линиями:
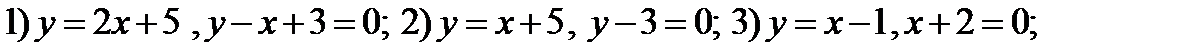
4. Доказать, что диагонали четырёхугольника с вершинами 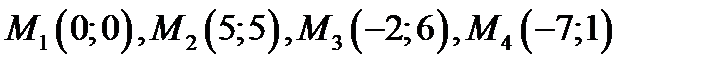 взаимно перпендикулярны.
взаимно перпендикулярны.
5. Дан эллипс 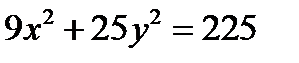 . Найти его
. Найти его
1) полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
Дать эскиз.
6. Дано уравнение гиперболы 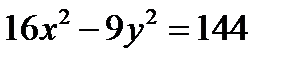 . Найти её
. Найти её
1) полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис; 5) уравнение асимптот.
7. Среди указанных пар векторов выбрать коллинеарные векторы
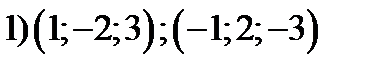 ;
; 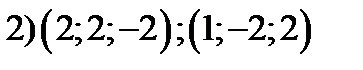 ;
; 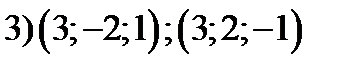
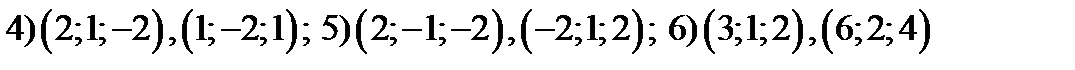
8. Вычислить: Единичный вектор в направлении вектора 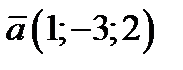
1) Вектор длины 3 в направлении вектора 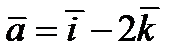
9. Используя калькулятор, вычислить расстояние от точки 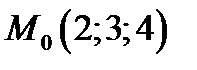 до
до
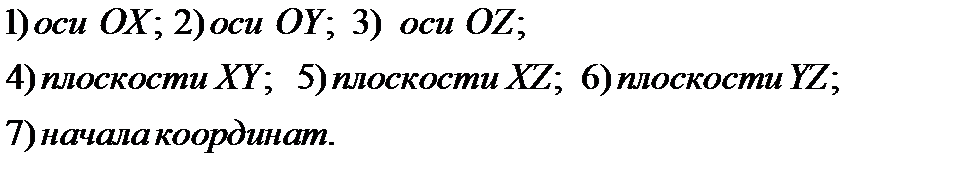
10. Концы отрезка 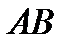 заданы координатами
заданы координатами 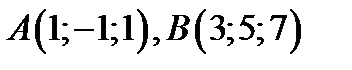 . На отрезке
. На отрезке 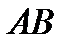
взята точка 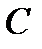 так, что отрезок
так, что отрезок 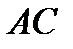 короче отрезка
короче отрезка 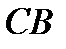 в два раза. Найти
в два раза. Найти
координаты точки  .
.
11. Среди векторов 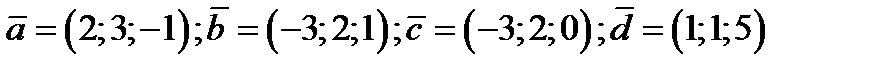 определить взаимно перпендикулярные векторы.
определить взаимно перпендикулярные векторы.
12. Используя скалярное произведение, вычислить:
1) проекцию вектора 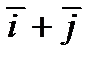 на вектор
на вектор 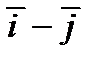 ;
;
13. Пусть задан вектор силы 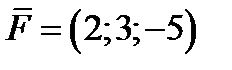 . Определить величину усилия от действия силы
. Определить величину усилия от действия силы 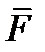 в заданных направлениях : 1)
в заданных направлениях : 1) 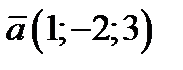 ; 2)
; 2) 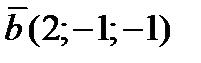 ; 3)
; 3) 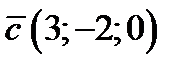
14. Найти вектор перпендикулярный двум векторам 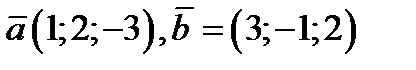 ;
;
15. Найти все векторы перпендикулярные векторам 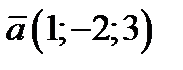 ,
, 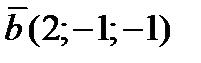 .
.
16. Вычислить 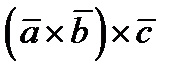 , где
, где 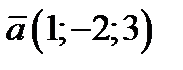 ,
, 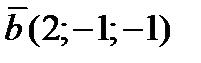 ,
, 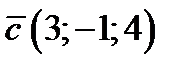
17. Вычислить площадь 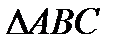 , где:
, где: 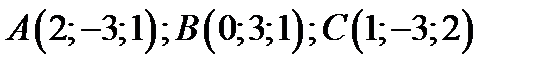
18. Для векторов 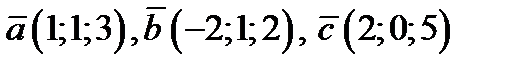 вычислить смешанное произведение
вычислить смешанное произведение
19. Лежат ли точки 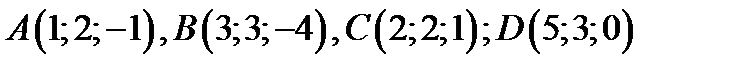 в одной и той же плоскости ?
в одной и той же плоскости ?
20. Вычислить объём пирамиды, если известны координаты её вершин
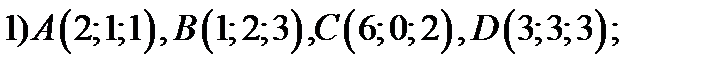
21. Написать уравнения плоскостей, удовлетворяющих условиям:
1) плоскость проходит через точку 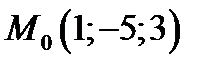 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору
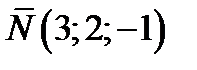 ;
;
2) плоскость проходит через точку 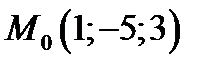 параллельно плоскости
параллельно плоскости 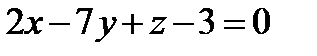 ;
;
3) плоскость проходит через точку 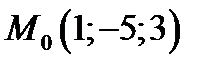 параллельно векторам
параллельно векторам
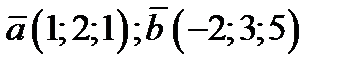 ;
;
4) плоскость проходит через точки 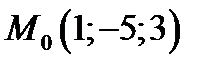 ,
, 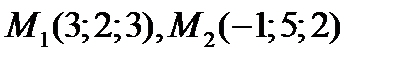 ;
;
22. Составить параметрические уравнения прямой, являющейся пересечением двух
плоскостей: 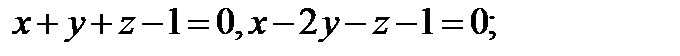
23. Составить параметрические уравнения прямой линии, проходящей через точку
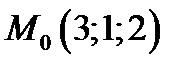 и
и
1) параллельно вектору 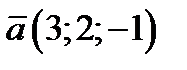 , 2) параллельно прямой линии
, 2) параллельно прямой линии
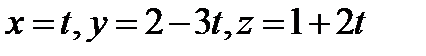 , 3) параллельно оси ОУ, 4) перпендикулярно плоскости
, 3) параллельно оси ОУ, 4) перпендикулярно плоскости 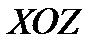 , 5) перпендикулярно плоскости
, 5) перпендикулярно плоскости 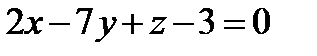 ,6)
,6)
точку 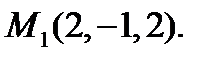
24. Вычислить значения функций, левые и правые предельные значения функций в точке 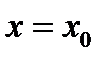
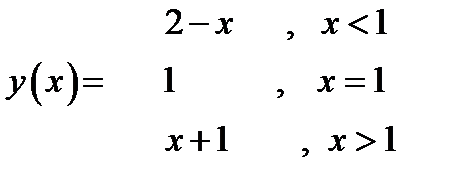 ,
, 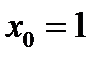
25. При каком значении параметра 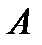 данные функции
данные функции 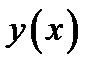 непрерывны
непрерывны
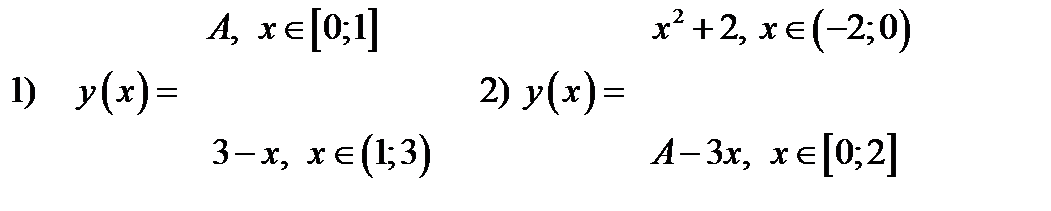
26. Исследовать данные функции на непрерывность и дать эскизы графиков
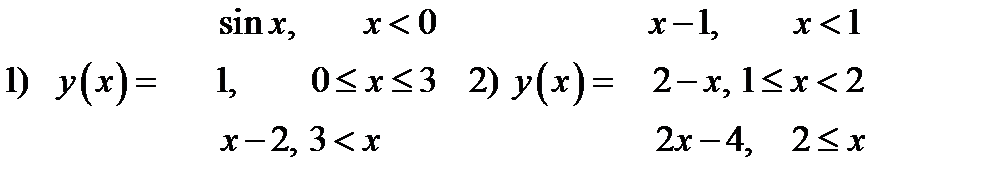
27. Используя правило Лопиталя или замечательные пределы найти предельные значения выражений
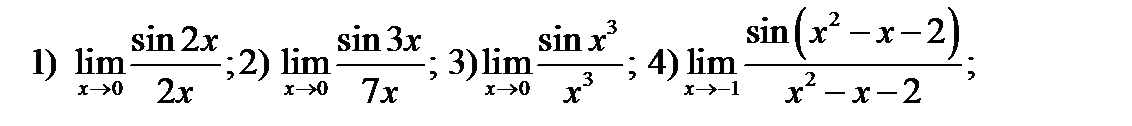
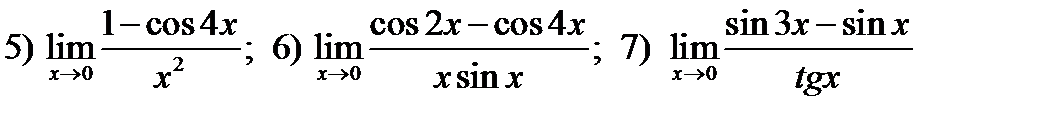 ;
;
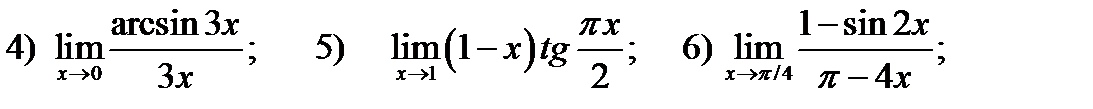
28. Написать уравнение касательной и нормальной прямой к функции 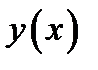 в точке
в точке 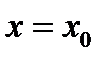 :
: 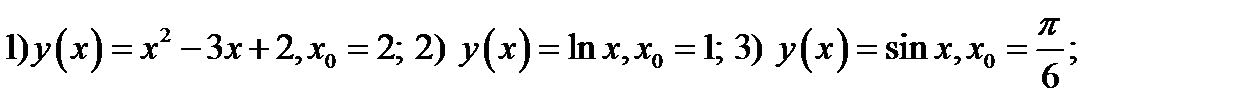
29. Найти угол между касательными, проведенными в точках 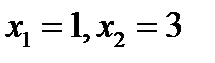 к графику функции
к графику функции 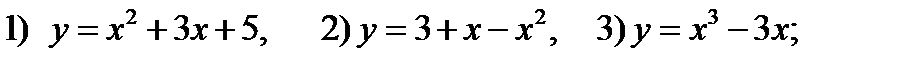
30. Вычислить производные функций
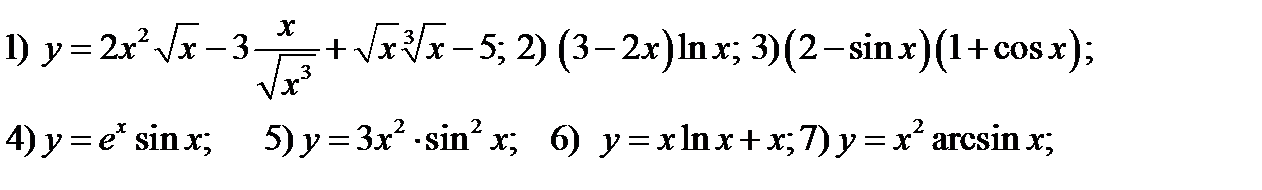
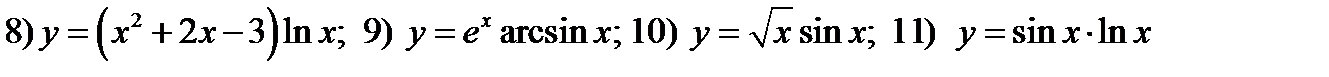
31. Вычислить производные функций
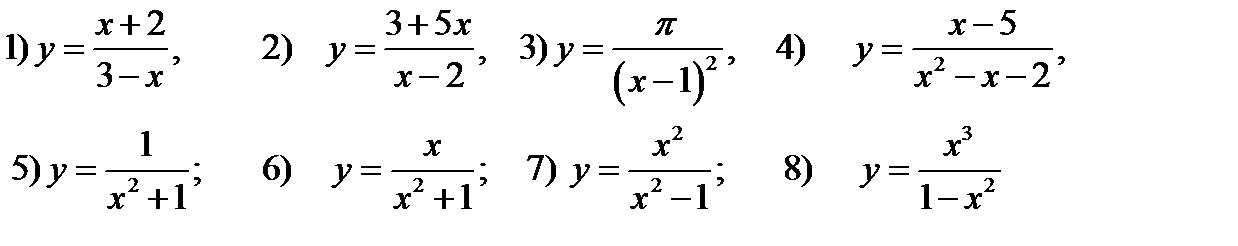
32. Найти вторые производные заданных функций
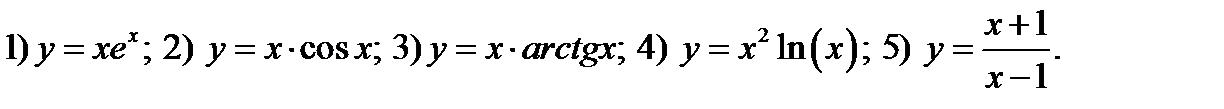
33. Применив цепное правило вычислить производные функций
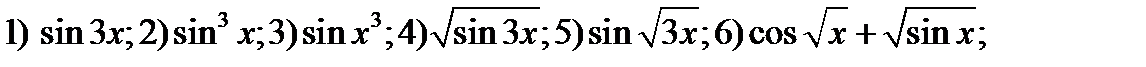
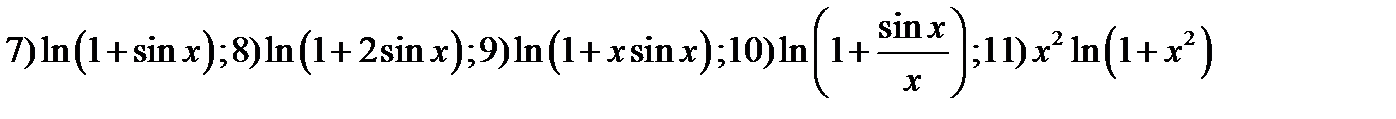 ;
;
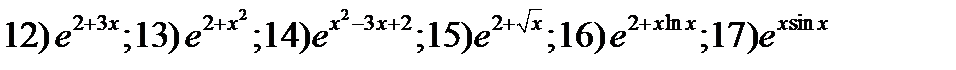 ;
;
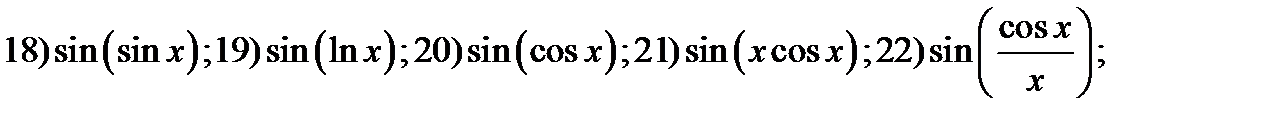
23) 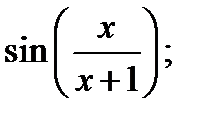
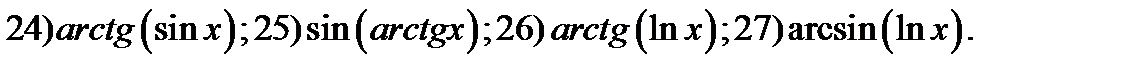
34. Применяя правило неявного дифференцирования, вычислить
производные от функций заданных неявно (уравнениями)
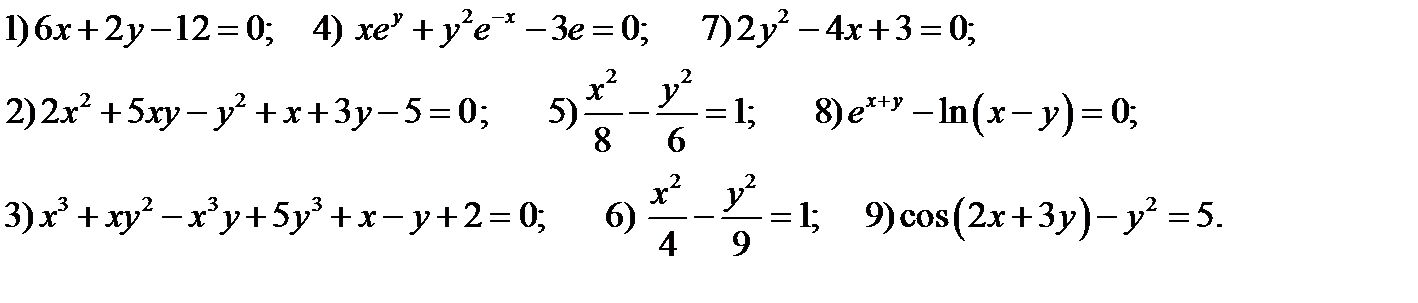
35. Вычислить и записать в параметрическом виде первую и вторую производные
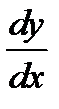 и
и 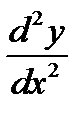 от функций
от функций 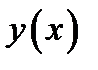 заданных в параметрическом виде
заданных в параметрическом виде 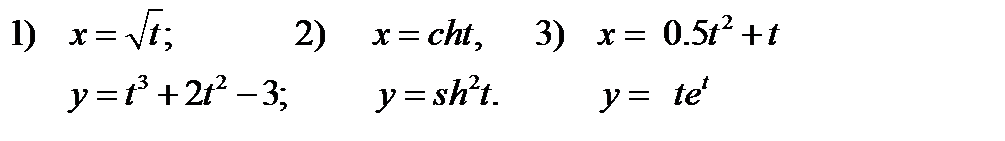 4)
4) 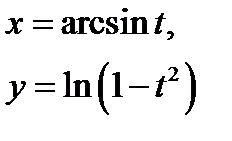
36. Написать уравнение касательной и нормали к кривым заданным = параметрическими уравнениями 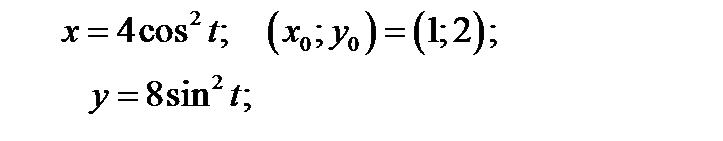
37. Написать формулу Лагранжа (о среднем в дифференцировании) для функций
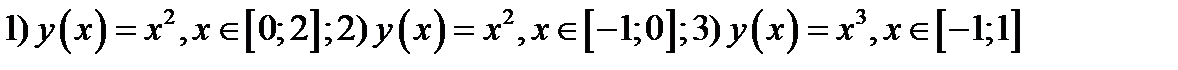
38. Используя правило Лопиталя, вычислить указанные пределы 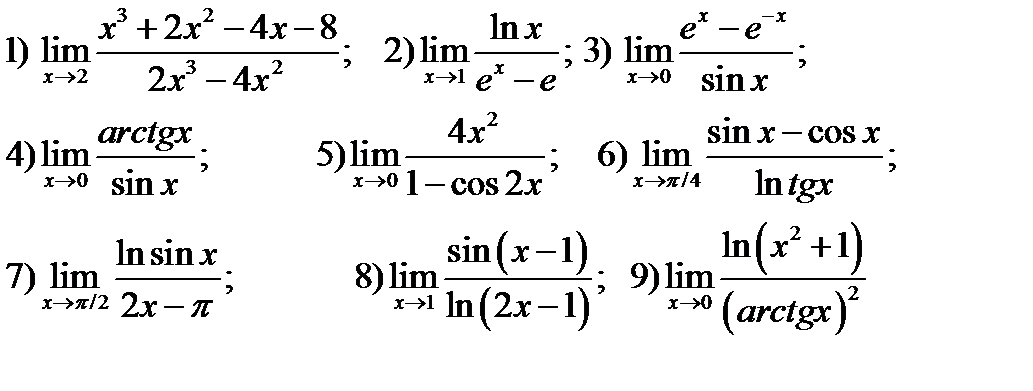
39. Написать уравнения горизонтальных и вертикальных асимптот и дать эскиз
графика функции
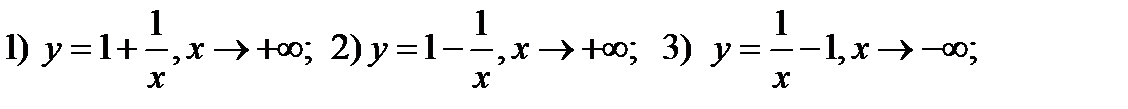
40. Изобразить на графике любую пару дифференцируемых функций 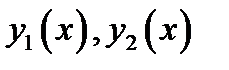 ,для которых
,для которых 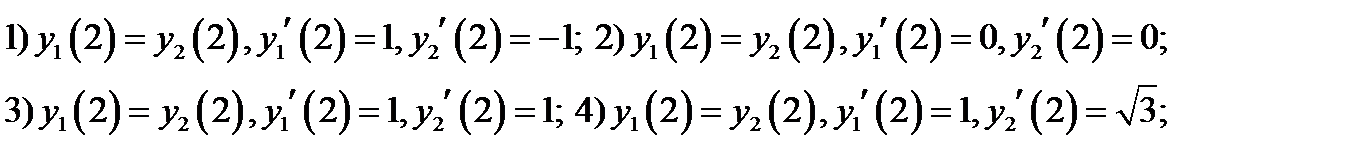
Cколько таких пар функций существует в каждой конкретной точке?
41. Определить интервалы возрастания и убывания функций 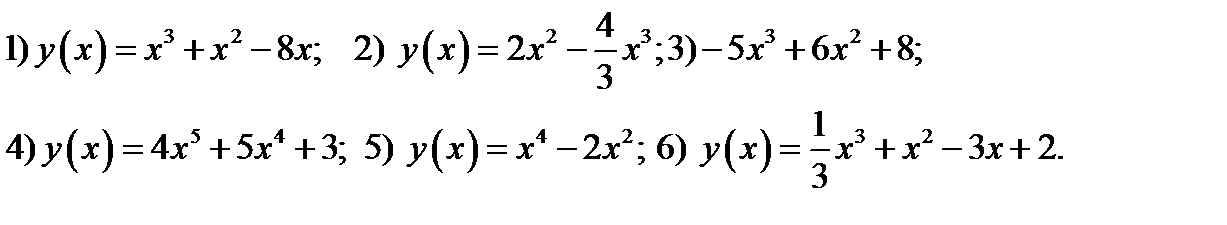
42. Определить интервалы возрастания и убывания функций
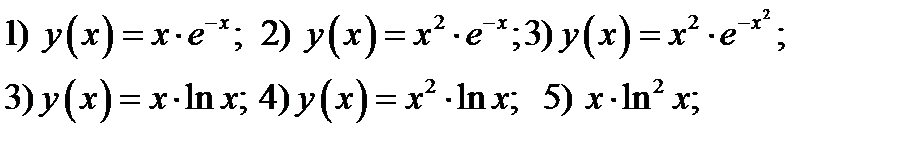
43. Определить локальные экстремумы функций
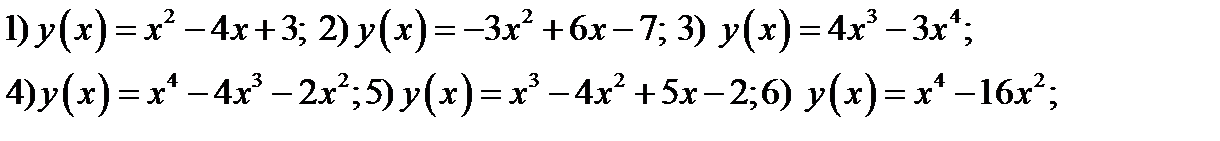
44. Доказать, что функция 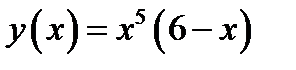 имеет локальный максимум в
имеет локальный максимум в
точке 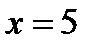 и не имеет экстремума в точке
и не имеет экстремума в точке 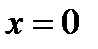 .
.
45. Найти точки перегиба графиков и интервалы выпуклости данных функций
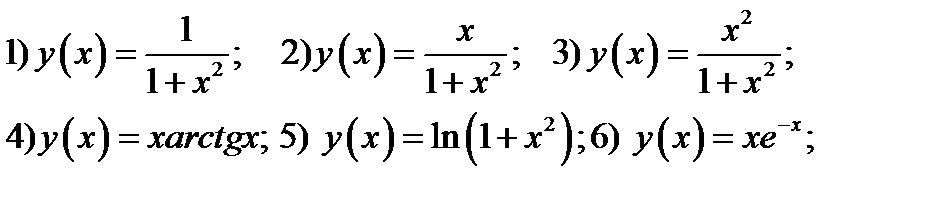
46. Доказать, что для графика функции 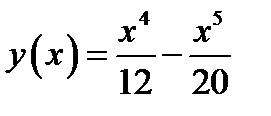 точка
точка 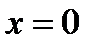 не является точкой перегиба, а точка
не является точкой перегиба, а точка 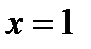 есть точка перегиба.
есть точка перегиба.
47. Число 8 разбить на два слагаемых так, чтобы их произведение было
наибольшим.
48.Найти на оси 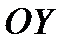 точку, для которой сумма квадратов расстояний от точек
точку, для которой сумма квадратов расстояний от точек
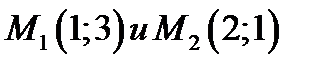 была бы наименьшей.
была бы наименьшей.
49.Среди прямоугольников, имеющих периметр 8м, найти прямоугольник
с наибольшей площадью.
283. Среди прямоугольных треугольников, имеющих одинаковую гипотенузу
 =10м, найти треугольник наибольшей площади.
=10м, найти треугольник наибольшей площади.
284.Прочность балки прямоугольного сечения прямо пропорциональна ширине
балки и квадрату её высоты. Определить параметры балки наибольшей
прочности, которую можно вырезать из бревна, диаметр которого 0.5м.
50. Пусть требуется построить цилиндрический бак объёмом 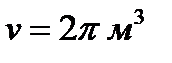 . Какими должны быть размеры бака, чтобы на его изготовление ушло как можно меньше листовой стали. Для расчётов принять
. Какими должны быть размеры бака, чтобы на его изготовление ушло как можно меньше листовой стали. Для расчётов принять 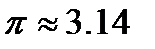 .
.
51. Из стального листа площадью 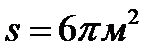 требуется изготовить цилиндр
требуется изготовить цилиндр
наибольшего объёма. Определить радиус и высоту такого цилиндра.
Для расчётов принять 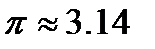 .
.
52. Среди всех прямых круговых конусов, у которых образующая равна 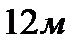 ,
,
найти радиус основания конуса наибольшего объёма.
Вариант пробный.
1) Вычислить определитель 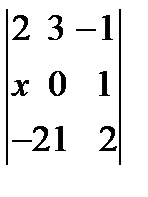 при
при 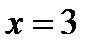 .
.
2) Решить систему линейных алгебраических уравнений
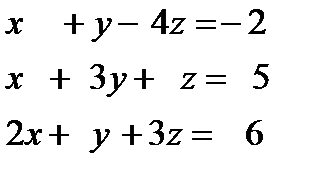
3)Лежат ли точки 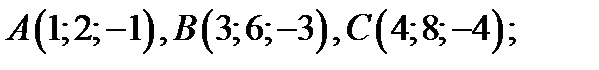 на одной и той
на одной и той
же прямой ?
4)Написать уравнение прямой , которая проходит через точку
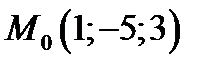 ,параллельно плоскости
,параллельно плоскости 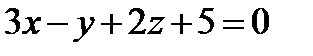 .
.
5)Н айти точку, в которой касательная к графику функции 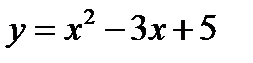
Наклонена к оси ОХ под углом 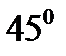 .
.
6) Вычислить производные функций
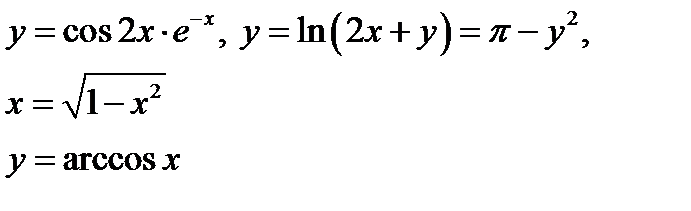
7)Дана гипербола 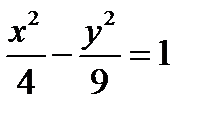 . Найти её
. Найти её
1)полуоси; 2) фокусы; 3) эксцентриситет; 4) асимптоты
8)Определить интервалы возрастания и убывания функции, точки локальных экстремумов
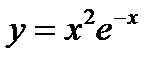 .
.
9)Найти точки перегиба графиков и интервалы выпуклости данных функций
1) 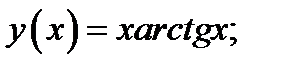
10) Используя правило Лопиталя , вычислить предельное значение 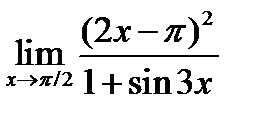 ;
;
