Поиск минимального остовного дерева
Пусть G = (V, Е) — связный взвешенный граф. Необходимо построить МОД в графе G, последовательно выбирая ребра наименьшего возможного веса до образования остовного дерева. МОД в памяти компьютера хранится в виде множества Т ребер.
Пример 9. В табл. 4.3 дано расстояние (в милях) между пятью деревнями А, В, С, D и Е. Найдите минимальное остовное дерево.
Таблица 4.3
| А | В | С | D | Е | |
| А | — | ||||
| В | — | ||||
| С | — | ||||
| D | — | ||||
| Е | — |
Решение. Ребра выбираются следующим образом: первое — ребро DE веса 2; второе — АС веса 3; третье — СЕ веса 7. На этой стадии строящееся дерево выглядит так, как на рис. 4.18.
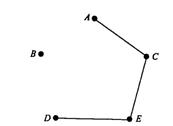Рис. 4.18. Вид дерева после трех шагов
Следующие по весу ребра - AD, AE и CD, каждое из которых имеет вес 9. Однако какое бы из них мы ни добавили, получится цикл. Поэтому перечисленные ребра следует исключить из числа доступных для строительства. Далее идут ребра ВС и BD веса 11. Можно присоединить любое из них, получив при этом два разных МОД: {АС, ВС, СЕ., DE} или {AC, BD, CE, DE} веса 23 каждое.
Зачастую нам хотелось бы иметь деревья, представляющие информацию с учетом естественной иерархической структуры, такие, как, например, генеалогическое древо (рис. 4.19.). На нем показаны некоторые члены семьи Бернулли, каждый из которых был известным швейцарским математиком.
Генеалогическое древо можно изобразить и более сжато. Схема, приведенная на рис. 4.20., представляет собой пример дерева с корнем. Корень, в некотором смысле, можно назвать величайшей вершиной (например, родоначальник математиков Бернулли). Вершины дерева, лежащие непосредственно под данной, называются сыновья. С другой стороны, вершина, стоящая непосредственно перед сыном, называется ее отцом.
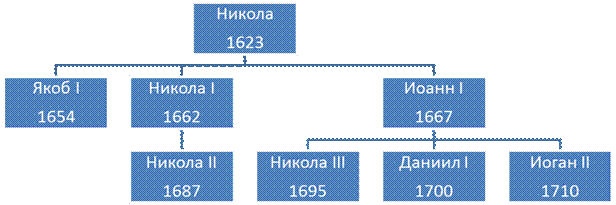
Рис. 4.19. Династия Бернулли
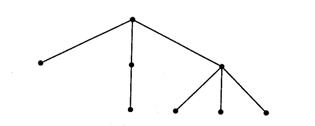
Рисунок 4.20. Схема генеалогического древа Бернулли
Дерево с корнем можно определить рекуррентным образом. Отдельная вершина является деревом с корнем (она же служит и корнем такого дерева). Если Т1 Т2, ..., Тk— несвязанные друг с другом деревья с корнями v1 ,v2,…, vk, то граф, получающийся присоединением новой вершины v к каждой из вершин v1 ,v2,…, vk отдельным ребром, является деревом Т с корнем v. Вершины v1 ,v2,…, vk графа Т — это сыновья корня v. Мы изображаем такое дерево с корнем, расположенным наверху, и сыновьями, стоящими ниже, непосредственно под корнем (см. рис. 23). Каждую вершину дерева с корнем можно рассматривать как корень другого дерева, которое «растет» из него. Мы будем называть его поддеревом дерева T.
Как мы уже говорили, вершина на самом верху дерева - его корень, а вот те, которые находятся в самом низу дерева (и не имеют сыновей) принято называть листьями. Остальные вершины, отличные от корня и листьев, называют внутренними.
Область применения деревьев с корнем обширна. Это, например, и информатика, и биология, и менеджмент. Для приложения к информатике наиболее важны так называемые двоичные или бинарные деревья с корнем. Двоичное дерево отличает от остальных то, что каждая его вершина имеет не более двух сыновей. В двоичном дереве скорнем вниз от каждой вершины идет не более двух ребер (См. Рис. 4.21).
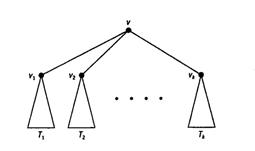Рис. 4.21.
Таким образом, можно сказать, что каждой вершине двоичного дерева с корнем соответствует не более, чем два поддерева, которые принято называть левым и правым поддеревьями этой вершины. Если оказалось, что у какой-то вершины дерева отсутствует потомок слева, то ее левое поддерево называют нулевым деревом (т.е. нулевое дерево — это дерево без единой вершины). Аналогично, если у вершины отсутствует правый потомок, то ее правое поддерево будет нулевым.
Пример 10.Пусть Т — двоичное дерево с корнем, изображенное на рис. 4.22.
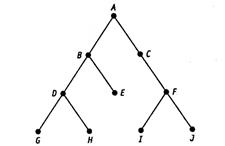
Рис. 4.22. Двоичное дерево с корнем T
Определите:
(а) корень Г;
(б) корень левого поддерева вершины В;
(в) листья Т;
(г) сыновей вершины С.
Нарисуйте двоичное дерево с корнем Т', полученное из Т перестановкой левых и правых поддеревьев у каждой вершины.
Решение.(а) А; (б) D; (в) G, H, E, I и J; (г) F.
Двоичное дерево с корнем Т' начерчено на рис. 4.23.
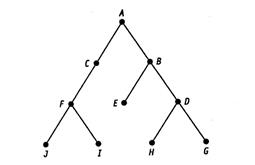
Рис. 4.23. Двоичное дерево с корнем Т’
Контрольные вопросы
1. Как зародилась теория графов? Кто является ее основоположником?
2. В каких областях человеческой деятельности используется теория графов?
3. Что называется графом?
4. В чем суть задачи о Кенигсбергских мостах?
5. Дать определение неориентированного, ориентированного и смешанного графа.
6. Дать определения вершин и ребер графа. Какие ребра называются кратными?
7. Что включает в себя понятие инцидентности вершин?
8. Какие вершины называются изолированными и висячими? Что такое петля?
9. Дать определение степени вершины.
10. Дать определение пути (маршрута) в графе.
11. В чем различие понятий простого графа, мультиграфа, псевдографа, нуль-графа, биграфа?
12. Определить понятия полного и двудольного графа.
13. Чему равны степени вершин полного графа?
14. Какой граф называется эйлеровым?
15. Что такое эйлеров цикл?
16. Какой граф называется гамильтоновым?
17. Что называется цепью (простой цепью)?
18. Что называется циклом (простым циклом)?
19. Что такое контур графа?
20. Дать определение матрицы смежности графа. Как составляется матрица смежности? Что она характеризует?
21. Определить понятия части графа, подграфа, суграфа?
22. Что такое ацикличный граф?
23. Что такое цепь, путь, дерево, лес?
24. Перечислите свойства деревьев.
25. Какой граф называется неориентированным деревом?
26. Что называется корневым деревом? Остовным деревом?
27. Что такое связный граф?
28. Что характеризует число связности графа?
29. Что такое вес ребра?
30. Дать определение глубины вершины, глубины дерева?
31. В чем суть алгоритма ближайшего соседа?
32. Как осуществляется поиск минимального остовного дерева?