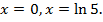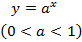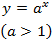Показательные уравнения
Функция вида 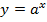 , где а – положительное число, не равное единице, называется показательной. Свойства показательной функции:
, где а – положительное число, не равное единице, называется показательной. Свойства показательной функции:
1)область определения – множество всех действительных чисел, 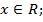
2) область значений – множество всех положительных чисел, 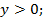
3) если 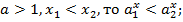
4) если 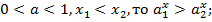
5) 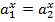 тогда и только тогда, когда
тогда и только тогда, когда 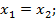
6) 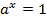 , если
, если 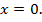
График показательной функции приведен на рис. 4.1.
|
|
|
|
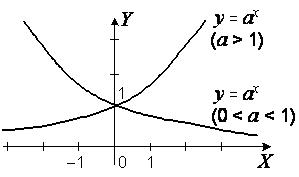
Рис. 4.1. График показательной функции.
Уравнения, содержащие переменную в показателе степени, называются показательными.
Уравнения вида 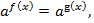 где
где 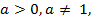
равносильны уравнению 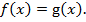 Если
Если 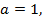 то решением являются все значения х, принадлежащие одновременно областям определения функций f (x) и g (x). Аналогично в случае а = 0,
то решением являются все значения х, принадлежащие одновременно областям определения функций f (x) и g (x). Аналогично в случае а = 0, 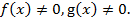
Пример 1. Решить уравнение: 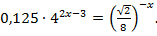
Решение. 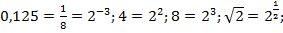 поэтому уравнение можно записать в виде:
поэтому уравнение можно записать в виде:
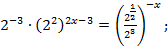
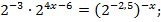
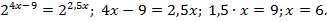
Ответ: x = 6.
Уравнения вида 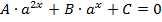 можно, заменив
можно, заменив 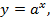 свести к квадратному (или линейному при А = 0) уравнению:
свести к квадратному (или линейному при А = 0) уравнению: 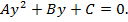
Пример 2. Решить уравнение : 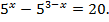
Решение. 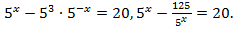
Обозначим 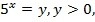 тогда
тогда
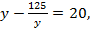
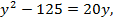
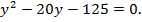
По теореме Виета 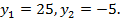
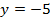 не удовлетворяет условию
не удовлетворяет условию 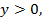 поэтому у = 25.
поэтому у = 25.
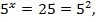 откуда х = 2.
откуда х = 2.
Ответ: х = 2.
Пример 3. Решить уравнение: 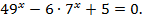
Решение. 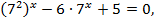
Обозначим 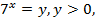 тогда
тогда 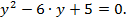
По теореме Виета 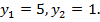
Если 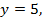 то
то 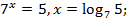
если 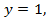 то
то 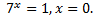
Ответ: 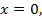 или
или 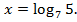
Уравнения вида 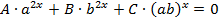 делением на b2х приводят к виду:
делением на b2х приводят к виду:
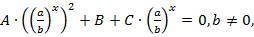 а затем заменой
а затем заменой 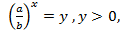 сводят к квадратному уравнению
сводят к квадратному уравнению 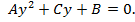
Пример 4. Решить уравнение :
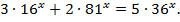
Решение . 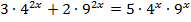
Разделим почленно уравнение на 92х:
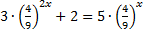
Обозначим 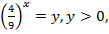 тогда
тогда
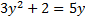 ,
, 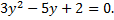
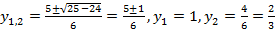
Если y = 1, то 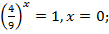 если
если 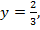
то 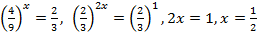
Ответ: 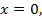 или
или 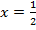
Пример 5. Решить уравнение:
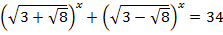
Решение. Поскольку 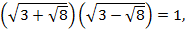 то
то 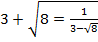 . Следовательно, если обозначить
. Следовательно, если обозначить 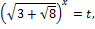 то исходное уравнение примет вид
то исходное уравнение примет вид 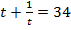 .
.
Уравнение 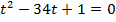 имеет два корня
имеет два корня
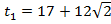 и
и 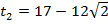 .
.
При 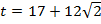 , получим уравнение,
, получим уравнение,
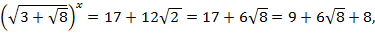
или 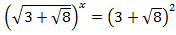 , откуда
, откуда 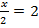 , х = 4.
, х = 4.
Если 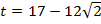 ,то получим уравнение,
,то получим уравнение,
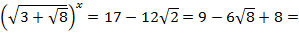
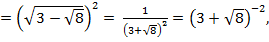
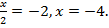
Ответ: х = 4, х = –4.
Пример 6. Решите уравнение:
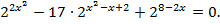
Решение. Примеры аналогичного типа предлагаются в вариантах ЕГЭ в разделе С. Поэтому решение должно быть достаточно подробным с указанием всех переходных моментов. Перепишем уравнение в виде
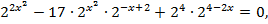 преобразуем
преобразуем 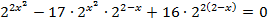 и введем замену
и введем замену 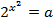 и
и 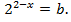 Теперь уравнение примет вид
Теперь уравнение примет вид 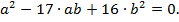
Такие уравнения называются однородными и всегда имеют нулевые решения 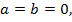 причём если
причём если 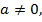 то и
то и 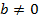 .
.
В силу замены, которую мы произвели, 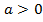 и
и 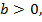 поэтому можно почленно разделить уравнение либо на а2, либо на b2. Разделим на b2 и получим:
поэтому можно почленно разделить уравнение либо на а2, либо на b2. Разделим на b2 и получим: 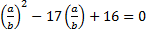 .
.
Пусть 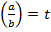 , тогда
, тогда 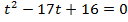 ,
, 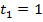 ,
, 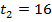 .
.
Если 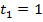 , то
, то 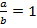 ,
, 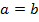 и
и 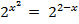 ,
,
откуда 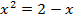 ,
, 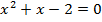 ,
, 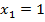 ,
, 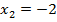 .
.
Если 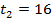 ,то
,то 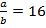 ,
, 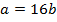 и
и 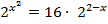
или 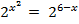 , откуда
, откуда 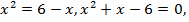
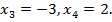
Ответ: 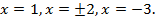
Замечание. В вариантах ЕГЭ иногда требуют пояснить переход от равенства 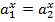 к равенству
к равенству 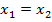 непрерывностью и монотонностью показательной функции.
непрерывностью и монотонностью показательной функции.
Пример 7. Решить уравнение:
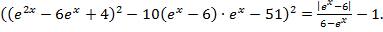
Решение. Выражение в правой части 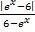 может принимать значения либо 1, либо (–1). Левая часть уравнения представляет собой квадрат некоторого действительного числа, поэтому не может принимать отрицательных значений. Следовательно, и правая часть уравнения неотрицательна.
может принимать значения либо 1, либо (–1). Левая часть уравнения представляет собой квадрат некоторого действительного числа, поэтому не может принимать отрицательных значений. Следовательно, и правая часть уравнения неотрицательна.
В силу этих рассуждений 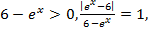 откуда
откуда 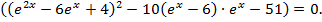 Обозначим
Обозначим 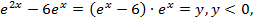 тогда
тогда 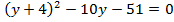 или
или 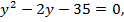
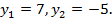
Значение 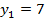 не удовлетворяет условию
не удовлетворяет условию 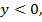 поэтому
поэтому 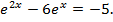
Заменив 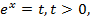 получим квадратное уравнение
получим квадратное уравнение 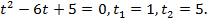
Если 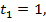 то
то 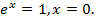
Если 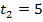 , то
, то 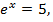
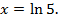
Ответ: