Доказательство свойства 1
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ
«Линейная алгебра»
для направления 080100 «Экономика»
Рязань 2012
Тема 2. Элементы матричной алгебры (20 часов, 10 лекций)
Лекция 1
Матрицы, виды матриц.
Операции над матрицами, их свойства.
Матрицы, виды матриц
Понятие матрицы появилось в связи с изучением СЛАУ впервые в середине 19 века в работах ирландского ученого У. Гамильтона и английских ученых А. Кэли и Дж. Сильвестра. Основы теории матриц созданы немецкими учеными К. Вейерштрассом и Т. Фробениусом. Название «матрица» происходит от латинского слова matrix (матрица), означающего «источник», «начало».
Определение 1.1. Матрица – это прямоугольная таблица, состоящая из 
строк и 
столбцов, элементами которой являются числа, функции или иные величины, над которыми можно производить алгебраические операции.
Обозначения:
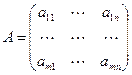или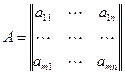 
,
где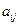 
– элементы матрицы;
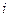– номер строки, 
;
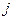– номер столбца, 
;
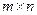– размер матрицы.
Если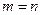 
, то матрица называется квадратной, тогда 
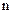– это порядок матрицы.
Пример 1.а)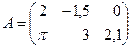 
размера 
.
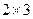б)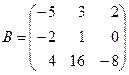 
– квадратная матрица 3-го порядка.
в)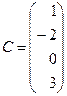 
– размера 
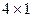(матрица-столбец).
г)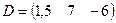 
– размера 
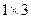(матрица-строка).
Определение 1.2. Главной диагональю квадратной матрицы называется воображаемая линия, соединяющая верхний левый угол с нижним правым. Элементы, стоящие на главной диагонали, называются диагональными. Воображаемая линия, соединяющая верхний правый и нижний левый углы, называется побочной диагональю.
Определение 1.3. Квадратная матрица, диагональные элементы которой равны 1, а остальные равны 0, называется единичной.
Например, единичная матрица третьего порядка имеет вид:
.
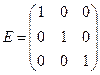Определение 1.4. Квадратная матрица, элементы которой, стоящие под главной диагональю, равны нулю, называется верхне-треугольной.
Операции над матрицами, их свойства
Операция сложения (вычитания).
Эти операции можно выполнять только над матрицами одного размера.
, 
,
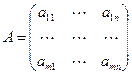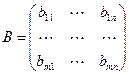тогда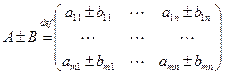 
.
Пример 1.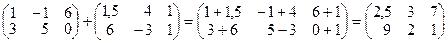 
.
Операция умножения матрицы на число.
Умножение матрицы 
размера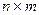 
на число 
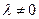– операция, в результате которой получается матрица 
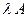, элементы которой равны элементам матрицы 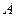, умноженным на число 
.
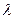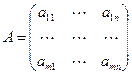, тогда 
.
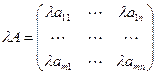Пример 2.Пусть в 1-й магазин в первый раз завезли 10 холодильников, 12 телевизоров и 8 стиральных машин, а во второй магазин – 5 холодильников, 20 телевизоров и 14 стиральных машин. Тогда общий завоз товаров в 1-й раз можно описать матрицей
.
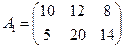Если во 2-й завоз поступление товаров в магазины описывается матрицей
,
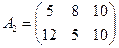то можно найти суммарный завоз товаров в магазины:
.
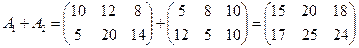Если завоз товаров в магазины, описываемый матрицей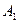 
, произведен троекратно, то результирующий завоз будет равен
.
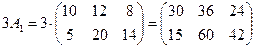Свойства операций
1. 
.
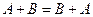2. 
.
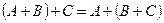3. 
.
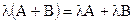4. 
.
5. 
.
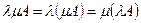Доказательство свойства 1
Пусть 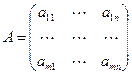, , 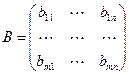тогда
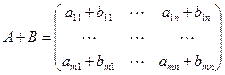и
.
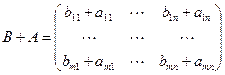Так как элементы этих матриц – числа, а сложение чисел обладает свойством коммутативности, то
, 
, .
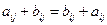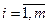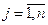Следовательно, 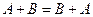.