Фундаментальная система решений

В предыдущем разделе было показано, что факт совместности или несовместности системы (6.6.1) можно установить, сравнив ранги ее основной и расширенной матриц. Рассмотрим теперь случай, когда система (12.5) совместна и найдем все ее решения.

При построении общего решения системы (12.5) воспользуемся следующими вспомогательными утверждениями.

Лемма 12.3 Любая линейная комбинация частных решений однородной системы (12.5) также является ее частным решением.

Лемма 12.4 Сумма некоторого частного решения однородной системы (12.5) и некоторого частного решения неоднородной системы является частным решением неоднородной системы (12.5).

Лемма 12.5 Разность двух некоторых частных решений неоднородной системы (12.5) является частным решением однородной системы (12.5).

Замечания 1°. Из лемм 12.3–12.5 следует, что

общее решение неоднородной системы уравнений есть общее решение однородной плюс некоторое частное решение неоднородной,и поэтому прежде всего необходимо найти общее решение однородной системы линейных уравнений.

2°. Однородная система линейных уравнений всегда совместна, поскольку у нее есть, по крайней мере, одно частное, называемое тривиальным, решение, для которого все неизвестные имеют нулевое значение.

3°. Поскольку частные решения системы линейных уравнений представимы в виде столбцов, то, используя операции сравнения, сложения и умножения на число для столбцов, а также лемму 12.3, можно ввести понятие линейной зависимости решений однородной системы линейных уравнений.

Теорема 12.10Однородная система (12.5) имеет 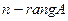линейно независимых частных решений.

Определение. Фундаментальной системой решений для системы линейных уравнений (12.5) называется совокупность любых 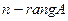частных, линейно независимых решений однородной системы (12.5), где 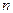– число неизвестных в системе (12.5), а 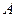– ее основная матрица.

Теорема 12.11Каждое частное решение однородной системы (12.5) может быть представлено в виде линейной комбинации частных решений, образующих фундаментальную систему решений.

Следствие 1. Общее решение неоднородной системы (12.5) может быть дано формулой

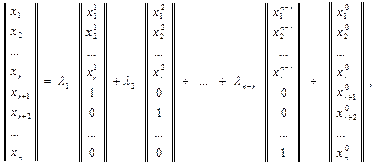
где

является некоторым частным решением неоднородной системы (12.5), а числа 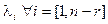– произвольные константы.

Следствие 2. Для того чтобы однородная система (12.5) с 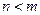имела ненулевое решение, необходимо и достаточно, чтобы ранг ее основной матрицы удовлетворял условию .

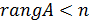В случае, когда основная матрица однородной системы (12.5) квадратная, условие существования нетривиального решения равносильно равенству .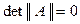

Теорема 12.12 (Фредгольма)Для того чтобы система (12.5) была совместной, необходимо и достаточно, чтобы каждое решение 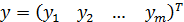сопряженной системы

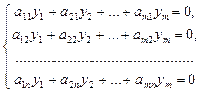
или в матричном виде

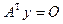
удовлетворяло условию

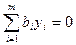
или в матричном виде

.

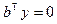Доказательство необходимости.

Пусть система уравнений (12.5) совместна, то есть для каждого ее решения 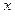справедливо равенство 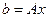. Найдем произведение 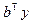в предположении, что

.

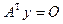Имеем

.

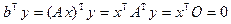Доказательство достаточности.

Пусть 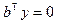для любого решения системы линейных уравнений 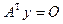. Тогда общие решения систем линейных уравнений 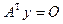и

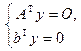
совпадают, и для этих систем максимальное число линейно независимых решений одинаково. Поэтому, согласно теоремам 12.10 и 12.11,

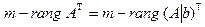или ,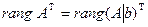

но поскольку ранг матрицы не меняется при ее транспонировании, то имеет место равенство 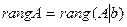, означающее в силу теоремы 12.9 (Кронекера-Капелли) совместность системы линейных уравнений .

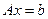Теорема доказана.