Задание для студентов
ПРАКТИЧЕСКАЯ РАБОТА № 6.
Тема: «Решение дифференциальных уравнений различных видов».
Теоретические сведения.
Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными.
1. Выражают производную функции через дифференциалы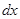 
и 
.
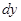2. Члены с одинаковыми дифференциалами переносят в одну сторону равенства и выносят дифференциал за скобку.
3. Разделяют переменные.
4. Интегрируют обе части равенства и находят общее решение.
5. Если заданы начальные условия, то находят частное решение.
Алгоритм решения дифференциального уравнения первого порядка.
1. Определить вид дифференциального уравнения первого порядка:
А)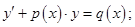 
Б) 
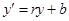, где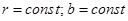 
.
2. В зависимости от вида уравнения выбрать алгоритм:
А.1. Используя подстановку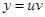 
, находят 
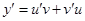и подставляют эти выражения в уравнение: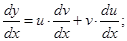 
Данное уравнение примет вид: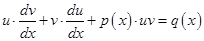 
.
А.2. Сгруппировать члены уравнения так, чтобы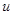 
вынести за скобку: 
. Из скобки, приравняв её к нулю, найти функцию 
.
А.3. Подставляют найденную функцию 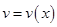в оставшееся выражение 
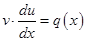и находят функцию 
.
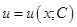А.4. Записывают общее решение, подставив выражения для найденных функци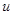й и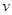 
в равенство : 
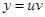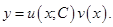
А.5. Если требуется найти частное решение, то определяют С из начальных условий и подставляют в общее решение.
Б.1. Определить значения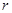 
и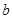 
, и записать общее решение в виде: 
.
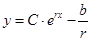Алгоритм решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами представим в виде таблицы.
| Дифференциальное уравнение |  | ||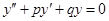
| Характеристическое уравнение |  | ||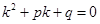
| Дискриминант |  |  |  |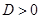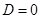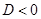
| Корни характеристического уравнения |  |  |  |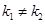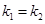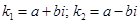
| Множества решений |  |  |  |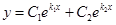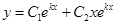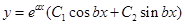
Задание для студентов.
Выбор параметров т и п.
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры зачетной книжки (студенческого билета) (А – предпоследняя цифра, В – последняя цифра) и выбрать из таблицы 1 параметр m, а из таблицы 2 выбрать параметр n. Эти выбранные два числа m и n нужно подставить в условия всех задач контрольной работы.
Таблица 1 (выбор параметра m)
| А | ||||||||||
| т |
Таблица 2 (выбор параметраn)
| В | ||||||||||
| п |
1. Найти общее решение уравнений:
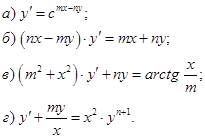
2. Составить уравнение: Скорость роста банковского вклада пропорциональна с коэффициентом, равным m, величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составила n миллионов рублей.
3. Решить задачу Коши:
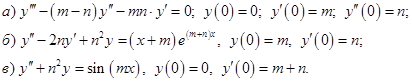
4. Найти общие решения дифференциальных уравнений:
а)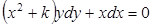 
;
б)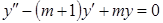 
;
в)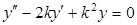 
.
Примеры решения задач:
Пусть m=6,n=7
1. Найти общее решение уравнений:
а)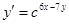 
; 
; 
; 
; 
; 
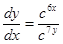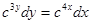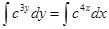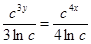
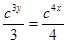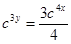- общий интеграл уравнения.
б)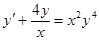 
Это уравнение Бернулли.
Положим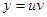 
. Подставляя в исходное уравнение , 
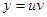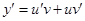, сгруппируем члены, содержащие 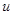в первой степени.
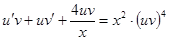
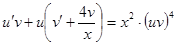
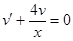
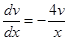
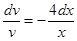
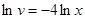
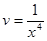
Для отыскания 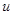имеем уравнение 
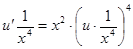. Разделяем переменные и интегрируем: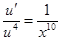 
; 
; 
; 
, 
.
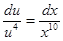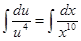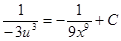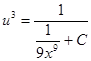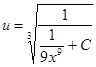Следовательно,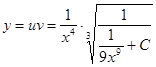 
2.Скорость роста банковского вклада пропорциональна с коэффициентом, равным m, величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составила n миллионов рублей.
Решение: m =4 и n=3
Скорость роста банковского вклада пропорциональна с коэффициентом, равным 4, величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составила 3 миллионов рублей.
По своему смыслу производная это скорость. Пусть банковский вклад – функция y(t).
Тогда согласно условию задачи получим дифференциальное уравнение:
,
,
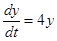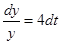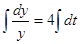
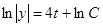
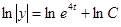
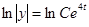
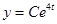
Значение величины С найдем из условий: y(0)=3.
, 
.
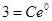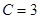Итак, закон изменения величины вклада со временем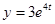 
.
3.Решить задачу Коши:
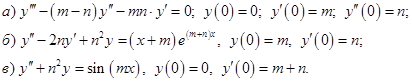
а)
;
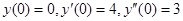
Решение:
Характеристическое уравнение имеет вид:
,
,
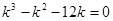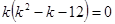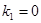или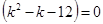 
, 
.
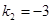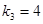Значит, общее решение уравнения имеет вид:
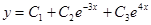
Частное решение уравнения найдем из условий:
.
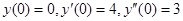Получаем систему:
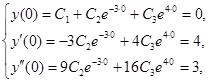
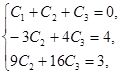
Решив систему, получим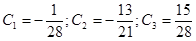 
.
Итак, частное решение уравнения: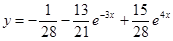 
.
б)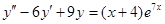 
, 
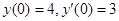
Решение:
Характеристическое уравнение имеет вид:
.
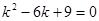Решение данного уравнения: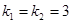 
.
Значит общее решение однородного уравнения: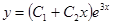
.
Общее решение неоднородного уравнения будем искать в виде:
.
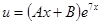Итак,
,
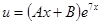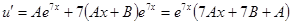
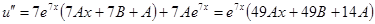
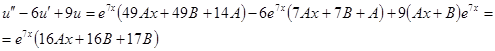
Таким образом, имеем систему: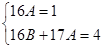 
, т.е. 
.
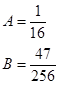в)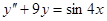 
, 
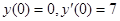
Решение:
Характеристическое уравнение имеет вид:
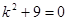. Решение характеристического уравнения: 
.
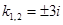Тогда общее решение однородного уравнения: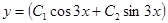 
.
Общее решение неоднородного уравнения будем искать в виде:
.
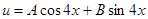Итак,
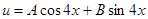
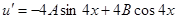
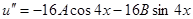
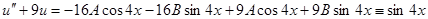
Таким образом, имеем систему: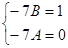 
, т.е. 
.
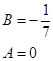Следовательно, общее решение данного уравнения имеет вид
.
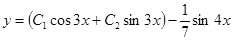Найдем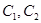 
, используя начальные условия .
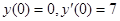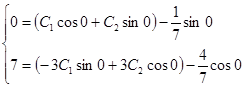или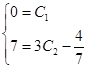 
.
Отсюда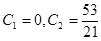 
, т.е.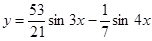 
4.Решить систему линейных уравнений с начальными условиями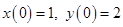 
:
.
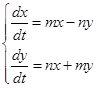Решение: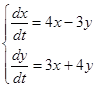 
Продифференцируем по t первое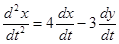 
; исключая из полученного уравнения 
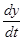и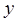 
, имеем 
, 
,
,
.
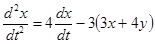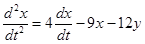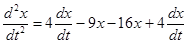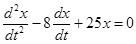Характеристическое уравнение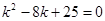 
имеет корни: 
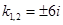. Следовательно, общее решение для х запишется в виде: 
.
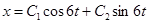Общее решение для у находим из первого уравнения:
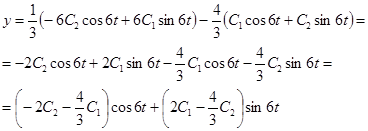
Итак, ,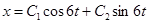 
.
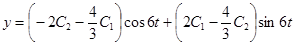Воспользуемся начальными условиями для нахождения произвольных постоянных: .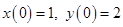
, 
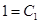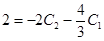
Отсюда: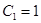 
, 
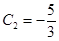. Таким образом, искомое решение имеет вид: 
, 
.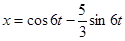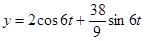