Решение систем линейных уравнений матричным методом
Определение матрицы, действия над матрицами.
Прямоугольная таблица, составленная из элементов (в частном случае чисел) и имеющая m строк и n столбцов, называется матрицей типа mxn.
Элементы матрицы А обозначаются 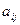 , где i – номер строки, а j – номер столбца, в пересечении которых находится элемент.
, где i – номер строки, а j – номер столбца, в пересечении которых находится элемент.
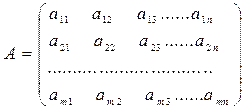
Если в матрице 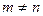 , то матрица называется прямоугольной.
, то матрица называется прямоугольной.
Если m=n, матрица называется квадратной. Для квадратной матрицы общее число строк или столбцов называют порядком матрицы.
Например, 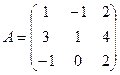 - квадратная матрица третьего порядка.
- квадратная матрица третьего порядка.
Матрица, имеющая только один столбец, то есть n=1, называется матрицей – столбцом (или вектором – столбцом).
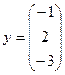 - трехмерный вектор – столбец.
- трехмерный вектор – столбец.
Для квадратных матриц вводятся понятия главной и побочной диагоналей.
Главная диагональ – это диагональ, проходящая чрез верхний левый и правый нижний углы матрицы. Побочная диагональ проходит через верхний правый и нижний левый углы матрицы.
Квадратная матрица, все элементы главной диагонали которой равны единице, а остальные равны нулю, называется единичной (Е).
Например, 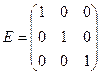 - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Две матрицы А и B называются равными, если они одинакового типа mxn и имеют равные соответствующие элементы, то есть 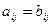 . Действия над матрицами одного типа рассматриваем на примере матриц А и B.
. Действия над матрицами одного типа рассматриваем на примере матриц А и B.
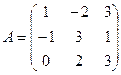 и
и 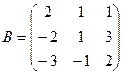
Сумма двух матриц А и B одинакового типа: C = A + B и 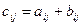 .
.
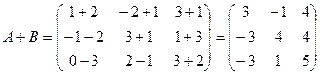
Разность матриц одинакового типа: D = A – B и 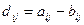
Произведение матрицы А на число k: L = Ak и 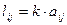
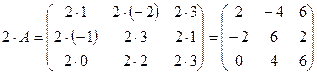
Произведение двух матриц AxB, типы которых mxn и pxq (n=p): C=AxB (матрица С имеет тип mxq) 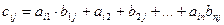 ,
,
То есть, 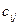 равно сумме произведений элементов i – той строки матрицы А на соответствующие элементы j –го столбца матрицы B.
равно сумме произведений элементов i – той строки матрицы А на соответствующие элементы j –го столбца матрицы B.
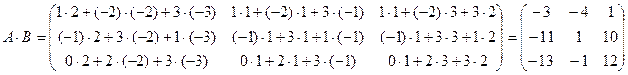
Следует отметить, что в общем случае 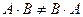 , поэтому нельзя менять местами множители.
, поэтому нельзя менять местами множители.
Определитель матрицы.
Понятие определителя связано с понятием квадратной матрицы. Определитель квадратной матрицы – это число, поставленное в соответствие данной матрице.
Обозначения определителя:
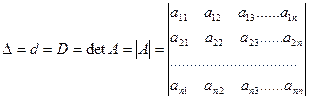
Рассмотрим правила вычисления определителей:
- Второго порядка
Определитель второго порядка равен разности произведений элементов главной и побочной диагоналей.
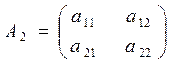 ,
, 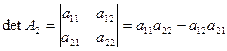
Например: 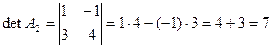 .
.
- Третьего порядка
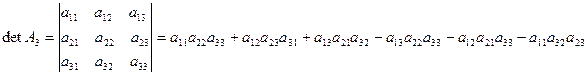
Например:
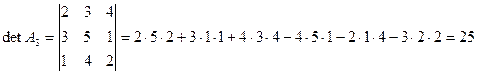
Рассмотрим такие понятия, как минор и алгебраическое дополнение элемента квадратной матрицы.
Минором элемента 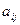 определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного вычеркиванием i-той строки и j-того столбца. Обозначается
определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного вычеркиванием i-той строки и j-того столбца. Обозначается 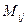 .
.
Алгебраическим дополнением элемента 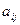 называется число
называется число 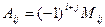 .
.
Например, найдем минор и алгебраическое дополнение элемента 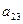 матрицы:
матрицы: 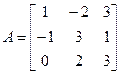
Решение:
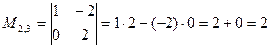
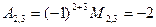
Справедлива теорема: определитель равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
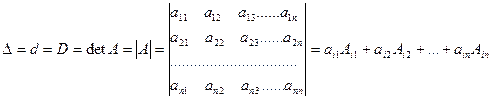
Эту формулу называют разложением определителя по элементам i-той строки.
