Отчет по лабораторной работе
ИЗУЧЕНИЕ ФИЗИЧЕСКОГО МАЯТНИКА.
Выполнили студенты группы Ф-11:
Олифенко Виталий и Болсун Леонид
ИЗУЧЕНИЕ ФИЗИЧЕСКОГО МАЯТНИКА
ЦЕЛЬ РАБОТЫ: исследование законов колебательного движения физического маятника и определение ускорения свободного падения методом Бесселя.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: установка FPM-04, линейка.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Физическим маятником (ФМ) называется твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси. Точка О пересечения этой оси (рис. 1) с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса.
Согласно основному уравнению динамики вращательного движения, в отсутствии сил сопротивления, уравнение движения ФМ имеет вид:
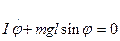 (1)
(1)
где I - момент инерции маятника относительно оси качания,
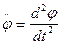 - угловое ускорение маятника,
- угловое ускорение маятника,
m - масса маятника,
l - расстояние от точки подвеса до центра масс маятника.
Ограничиваясь случаем малых углов ( 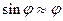 ) из (1) имеем
) из (1) имеем
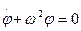 (2)
(2)
где введено обозначение 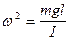
Нетрудно убедится, что решением записанного дифференциального уравнения (2) является функция
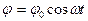
т.е. угол j отклонения ФМ от вертикали изменяется по гармоническому закону. Следовательно период колебаний ФМ равен
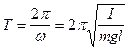 (3)
(3)
Как известно, период математического маятника
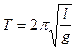 (4)
(4)
Сравнивая (3) и (4) находим, что ФМ колеблется с тем же периодом, что и математический, имеющий длину
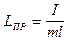 (5)
(5)
Длина математического маятника 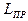 , имеющего тот же период колебаний, что и данный ФМ, называется приведённой длиной физического маятника.
, имеющего тот же период колебаний, что и данный ФМ, называется приведённой длиной физического маятника.
Момент инерции тонкого стержня относительно оси, проходящей через центр масс С перпендикулярно плоскости рисунка, равен 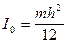 . По теореме Штейнера находим, что момент инерции стержня относительно оси качаний
. По теореме Штейнера находим, что момент инерции стержня относительно оси качаний
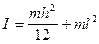 (6)
(6)
Подставим (6) в (4) и (5), приходим к соотношению
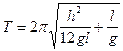 (7)
(7)
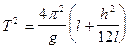 (8)
(8)
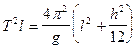 (9)
(9)
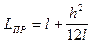 (10)
(10)
удобном для анализа и экспериментальной проверки. В частности, из анализа на экстремум функции (7) следует, что при
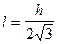 (11)
(11)
период Т физического маятника является минимальным.
ВЫПОЛНЕНИЕ РАБОТЫ
Упражнение № 1. Проверка формулы периода колебаний и определение приведённой длины физического маятника.
1. Таблица 1. Измерение времени 10 полных колебаний физического маятника, вычисление периода его колебаний.
| № опыта | среднее | |||||||
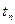 , с , с | 11,719 | 11,693 | 11,710 | 11,995 | 11,676 | 11,697 | 11,751 | 11,749 |
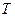 , с , с | 1,1719 | 1,1693 | 1,1710 | 1,1995 | 1,1676 | 1,1697 | 1,1751 | 1,1749 |
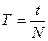 ,
, 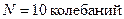
2. Длина физического маятника 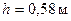 ,
,
Расстояние от центра тяжести до точки подвеса 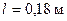 .
.
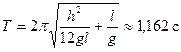 .
.
3. 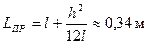 .
.
4. Таблица 2. Измерение времени 10 полных колебаний математического маятника, вычисление периода его колебаний.
| № опыта | среднее | |||||||
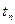 , с , с | 11,571 | 11,584 | 11,684 | 11,582 | 11,611 | 11,658 | 11,71 | 11,629 |
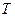 , с , с | 1,1571 | 1,1584 | 1,1684 | 1,1582 | 1,1611 | 1,1658 | 1,171 | 1,1629 |
5. Вывод: Из проведенных опытов очевидно, что формула 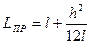 справедлива:
справедлива: 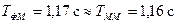 .
.
Упражнение № 2. Исследование формулы периода колебаний физического маятника.
1. Опорную призму устанавливаем на расстоянии 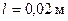 от центра масс стержня.
от центра масс стержня.
2. Таблица 3. Измерение времени 10 полных колебаний физического маятника, вычисление периода его колебаний.
| № опыта | среднее | |||||||
 , с , с | 32,28 | 32,24 | 32,40 | 32,34 | 32,29 | 32,36 | 32,29 | 32,31 |
 , с , с | 3,228 | 3,224 | 3,240 | 3,234 | 3,229 | 3,236 | 3,229 | 3,231 |
3. Таблица 4. Период колебаний физического маятника для различных значений 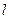 .
.
| № опыта | 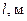 | 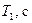 | 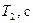 | 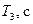 | 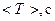 |
| 0,02 | 3,23 | 3,22 | 3,24 | 3,23 | |
| 0,03 | 1,88 | 1,87 | 1,86 | 1,87 | |
| 0,04 | 1,67 | 1,67 | 1,68 | 1,673 | |
| 0,05 | 1,52 | 1,54 | 1,53 | 1,53 | |
| 0,06 | 1,43 | 1,43 | 1,43 | 1,43 | |
| 0,07 | 1,36 | 1,37 | 1,37 | 1,363 | |
| 0,08 | 1,31 | 1,31 | 1,32 | 1,313 | |
| 0,09 | 1,27 | 1,28 | 1,27 | 1,273 | |
| 0,1 | 1,23 | 1,25 | 1,24 | 1,24 | |
| 0,11 | 1,22 | 1,21 | 1,21 | 1,213 | |
| 0,12 | 1,19 | 1,2 | 1,2 | 1,196 | |
| 0,13 | 1,18 | 1,18 | 1,19 | 1,183 | |
| 0,14 | 1,18 | 1,18 | 1,18 | 1,18 | |
| 0,15 | 1,17 | 1,17 | 1,18 | 1,173 | |
| 0,16 | 1,17 | 1,17 | 1,17 | 1,17 | |
| 0,17 | 1,17 | 1,17 | 1,16 | 1,166 | |
| 0,18 | 1,17 | 1,18 | 1,18 | 1,176 | |
| 0,19 | 1,18 | 1,18 | 1,18 | 1,18 |
4. График зависимости периода 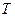 колебаний ФМ от длины
колебаний ФМ от длины 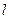 .
.
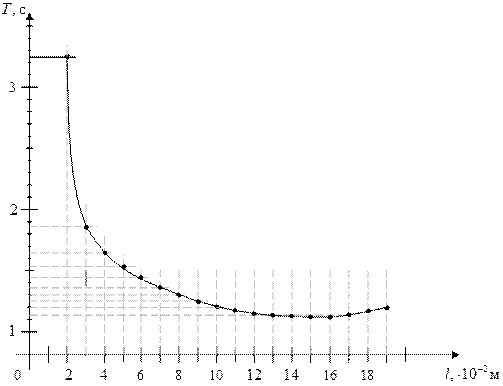
Из графика видно, что минимальное значение периода колебаний ФМ при 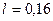 м.
м.
5. Сравним экспериментальное значение 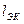 для минимального периода колебаний с теоретическим значением
для минимального периода колебаний с теоретическим значением 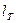
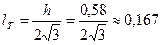 м.
м.
6. Таблица 5. зависимость 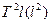
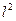 | 0,0004 | 0.0016 | 0,0036 | 0,0064 | 0,01 | 0,0144 | 0,0196 | 0,0256 |
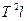 | 0,114 | 0,119 | 0,127 | 0,136 | 0,153 | 0,171 | 0,192 | 0,213 |
7. График зависимости 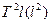
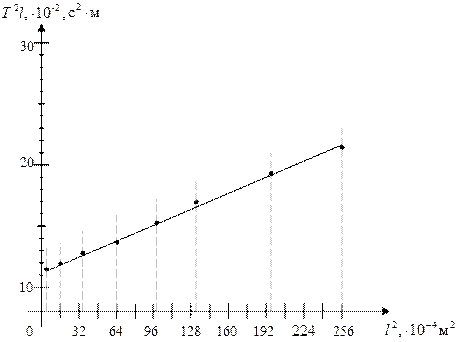 |
Вывод: Из графика видно, что зависимость 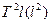 действительно является линейной.
действительно является линейной.
