Пересечение поверхностей вращения. Способ вспомогательных концентрических сфер. Теорема Монжа
Пересечение проецирующих тел вращения
Рассмотрим пересечение двух цилиндров (рис. 9.7), ось вращения одного из которых перпендикулярна горизонтальной плоскости проекций, а другого - профильной.
Поверхности цилиндров относятся к поверхностям второго порядка. Следовательно, линия их пересечения будет пространственной кривой четвертого порядка.
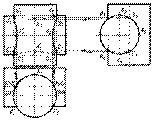
Рис. 9.7.
Вертикальный цилиндр проецируется на виде сверху в окружность. Так как линия пересечения принадлежит одновременно двум цилиндрам, то дуга F1'D1'B1'A1B1D1F1 является горизонтальной проекцией линии пересечения. Горизонтальный цилиндр проецируется в окружность на виде слева. Следовательно, дуга А3В3D3F3F3С3А3' является профильной проекцией линии пересечения.
На рис. 9.7 построены проекции характерных точек, которые находятся на пересечении линий связи, проведенных от вида сверху и от вида слева. Для более точного проведения фронтальной проекции линии пересечения следует построить также проекции промежуточных точек.
Метод вспомогательных секущих плоскостей.
Вспомогательные секущие плоскости чаще всего выбирают проецирующими и параллельными одной из плоскостей проекций - плоскостями уровня.
Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:
1. Если образующие (окружности) расположены в общих плоскостях уровня;
2. Если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;
3. Линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.
| Пример1:Рассмотрим построение линии пересечения треугольной призмы с конусом (рис.8.31) . Пусть ось вращения конуса перпендикулярна плоскости П1, а грани призмы перпендикулярны плоскости П2. В этом случае призму можно рассматривать, как три плоскости α, β, γ, проходящие через ее грани, а задача сводится к нахождению линий пересечения этих плоскостей с конусом. При этом в соответствии с характерными сечениями конуса известно, что плоскость α пересекает конус по окружности параллельной П1, β- по гиперболе параллельной П3, а γ- по эллипсу. На плоскость П2 линии пересечения от всех плоскостей проецируются в прямые, совпадающие со следами плоскостей α, β, и γ. Для построения проекций этих линий на плоскости П1 и П3 отметим характерные точки на уже имеющейся фронтальной проекции линий пересечения: | |
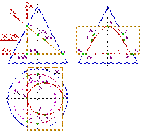
| Рисунок 8.31. Пересечение конуса и призмы |
Точки 12 и 62 – пересечения плоскости γ с очерком проекции конуса на плоскость П2 (главным меридианом), эти точки определяют положение большой оси эллипса, кроме того точка 12 –проекция точки вершины гиперболы и одновременно принадлежит конусу (лежит на очерке фронтальной проекции конуса) и ребру призмы (линии пересечения плоскостей α и β), а точка 62- проекция точки, одновременно принадлежащей конусу и ребру призмы (линии пересечения плоскостей α и γ); точки 2, 3, 7и8 – характерны тем, что их профильные проекции лежат на очерке проекции конуса; 42, 52- точки, лежащие на середине отрезка 1262(большой оси эллипса) и определяют положение малой оси эллипса; 9,10 – точки одновременно принадлежащие конусу и ребру призмы (образованному пересечением плоскостей α и β).
Рассмотрим последовательность нахождения проекций точек 4и5.Через фронтальные проекции этих точек проведем вспомогательную секущую плоскость φ.Эта плоскость пересекает конус по параллели p, а грань призмы по прямой линии m, параллельной ребру. На горизонтальной плоскости проекций пересечение p 1и m 1 определяют положение точек 41 и 51. Для точного построения кривых линий пересечения поверхностей обозначенных точек не достаточно. После нахождения проекций всех точек их необходимо соединить с учетом видимости.
| С тетрадки: |
Пересечение прямой с поверхностью вращения
В случае поверхности вращения секущих плоскостей выбираем таким образом, чтобы в сечении получалось пространственная фигура, окружность для конуса это может быть треугольник когда секущая плоскость проходит через вершину, для цилиндра параллелограмм когда секущая плоскость проходит параллельно оси цилиндра, поэтому секущая плоскость вспомогательной не всегда спроецирована но и общего положения. Боковая поверхность прямого кругового цилиндра является горизонтальной проецирующей, поэтому проецирующей точек пересечения можем определить на горизонтальной проекции.
