Показательные и логарифмические неравенства
Решите неравенства:
1. 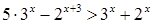 ;
;
2. 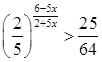 ;
;
3. 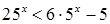 ;
;
4. 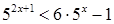 ;
;
5. 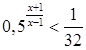 ;
;
6. 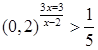 ;
;
7. 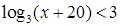 ;
;
8. 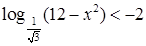 ;
;
9. 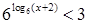 ;
;
10. 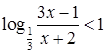 ;
;
11. 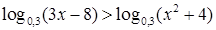 ;
;
12. 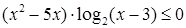 .
.
Примерные контрольные задания по разделам.
Раздел 1. РАЗВИТИЕ ПОНЯТИЕ О ЧИСЛЕ.
1. Укажите одно рациональное и одно иррациональное число:
а. принадлежащее промежутку 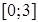 ;
;
б. не принадлежащее промежутку 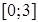 .
.
2. Сравните числа:
а. 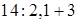 и
и 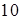 ;
;
б. 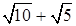 и
и 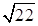 .
.
3. Приведите (если это возможно) пример прямоугольника, у которого:
а. и периметр, и площадь выражаются иррациональными числами;
б. периметр – иррациональное число, а площадь – рациональное число;
в. периметр – рациональное число, а площадь – иррациональное число;
г. и периметр, и площадь выражаются рациональными числами.
4. Решите уравнения на множестве действительных чисел:
а. 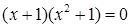 ;
;
б. 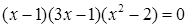 .
.
5. Решите уравнения на множестве комплексных чисел:
а. 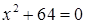 ;
;
б. 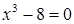 .
.
6. Выяснить, замкнуты ли относительно операций сложения, вычитания, умножения и деления множества:
а. целых чисел, кратных трем;
б. 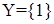 .
.
7. Вычислите:
а. 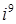
б. 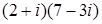
Раздел 2. ФУНКЦИИ, ИХ СВОЙСТВА И ГРАФИКИ.
Задание № 1
Функция 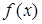 задана графически. Исследуйте функцию. Укажите:
задана графически. Исследуйте функцию. Укажите:
а. область определения;
б. множество значений;
в. промежутки монотонности (промежутки возрастания и убывания);
г. нули функции;
д. промежутки знакопостоянства;
е. является ли эта функция четной, нечетной или общего вида;
ж. точки экстремума, экстремумы функции;
з. наибольшее и наименьшее значения функции;
и. значения 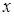 , при которых значение функции равно 1;
, при которых значение функции равно 1;
к. чему равны 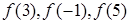 (по графику);
(по графику);
л. при каких значениях 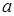 , уравнение
, уравнение 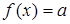 :
:
- не имеет корней;
- имеет один корень;
- имеет два корня.
Задание № 2
1. Постройте график функции, найдите множество значений, промежутки возрастания, убывания, точки экстремума.
а. 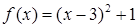 ;
;
б. 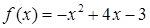 ;
;
в. 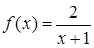 ;
;
г. 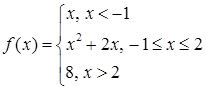
2. Найдите область определения функции:
а. 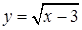 ;
;
б. 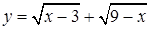 ;
;
в. 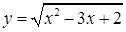 ;
;
г. 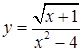 .
.
3. Исследуйте функцию на четность/нечетность.
а. 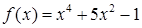 ;
;
б. 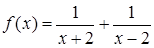 ;
;
в. 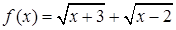 .
.
Раздел 3. КОРНИ, СТЕПЕНИ, ЛОГАРИФМЫ.
Задание № 1
1. Значение 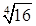 равно:
равно:
| а. 4 | б. 2 | в. 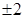 | г. 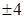 |
2. Область значений функции  :
:
а. 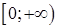 | б. 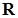 | в. 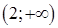 | г. 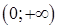 |
3. Убывающей является функция:
а. 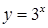 | б. 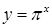 | в. 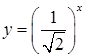 | г. 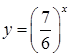 |
4. Решением уравнения 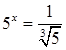 является число:
является число:
а. 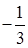 | б. 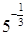 | в.  | г. 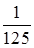 |
5. Значение 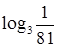 равно:
равно:
а. 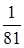 | б. 4 | в. 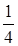 | г. 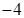 |
6. Найдите область определения функции 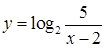 :
:
а. 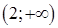 | б. 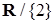 | в. 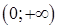 | г. 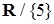 |
7. Множеством решений неравенства 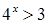 является промежуток:
является промежуток:
а. 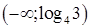 | б. 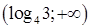 | в. 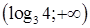 | г. 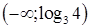 |
8. Положительным является число:
а. 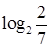 | б. 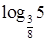 | в. 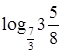 | г. 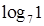 |
9. Решением уравнения 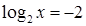 является:
является:
а. 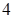 | б. 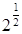 | в. 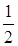 | г. 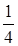 |
10. Справедливо ли, что
а. 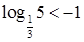 | б. 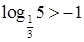 | в. 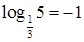 | г. нельзя сравнить |
Задание № 2
1. Постройте эскиз графика функции:
а. 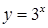 ;
;
б. 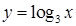 .
.
2. Сравните числа:
а. 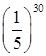 и
и 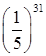 ;
;
б. 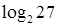 и
и 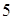 .
.
3. Решите уравнения:
а. 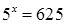 ;
;
б. 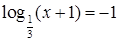 ;
;
в. 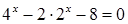 ;
;
г. 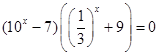 .
.
д. 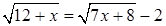
4. Вычислите:
а. 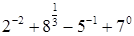 ;
;
б. 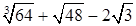 ;
;
в. 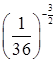 ;
;
г. 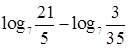 .
.
5. Решите неравенства:
а. 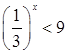 ;
;
б. 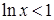 .
.
