Контрольные задания по курсу «Основы Дискретной Математики»

Вариант № 1

1. Позиционные системы счисления. Примеры.

2. Машина Тьюринга. Принципы функционирования.

3. Перевести из десятичной системы счисления в двоичную 132.

4. В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт и коробку конфет?

5. Запись чисел со знаком в заданном формате.

6. Способы задания булевой функции.

7. Перевести из двоичной системы счисления в четверичную 1001.

8. Изобразить на координатной плоскости множество, координаты (x,y) точек которого удовлетворяют условию: .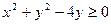

9. Определить, является ли функция монотонной?

f(x,y)=(x

10. Определить, является ли функция линейной?

f(x,y,z)=xyz

11. Является ли функция самодвойственной?

f(x,y,z)=(xy)

12. Полна ли система функций?

{x+y, x 1}

13. Построить полином Жегалкина для функции:

f(x,y)=(x+y)

14. Построить СДНФ для функции

f(x,y,z)=(x

15. Построить СКНФ для функции

f(x,y,z)=(x

16. Построить множество всех подмножеств P(M), если

M={a, {a,2},2}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(1,1),(2,2),(3,3),(4,4),(1,3), (3,1),(2,4),(4,2)}

Вариант № 2

1. Двоичная система счисления. Операции в этой системе.

2. Посредством машины Тьюринга реализовать алгоритм вычитания.

3. Перевести из десятичной системы счисления в двоичную 127.

4. В спортивном лагере 65 % ребят умеют играть в футбол, 70 % - в волейбол и 75 % - в баскетбол. Каково наименьшее число ребят, умеющих играть и в футбол, и в волейбол, и в баскетбол?

5. Запись чисел с плавающей точкой.

6. Основные операции алгебры логики.

7. Перевести из двоичной системы счисления в восьмеричную 101010.

8. А – множество делителей числа 12; В – множество корней уравнения ; С – множество нечетных чисел x таких, что .

9. Определить, является ли функция монотонной?

f(x,y)=(xy )

10. Определить, является ли функция линейной?

f(x,y)=(xy )

11. Является ли функция самодвойственной?

f(x,y)=(xy )

12. Полна ли система функций?

{x+y, x }

13. Построить полином Жегалкина для функции:

f(x,y)=(xy )

14. Построить СДНФ для функции

f(x,y)=(xy )

15. Построить СКНФ для функции

f(x,y)=(xy )

16. Построить множество всех подмножеств P(M), если

M={b, {a,2},a}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(1,1),(2,3),(3,3),(4,3),(1,3),(3,1),(2,4),(4,2)}

Вариант № 3

1. Четверичная система счисления, операции в этой системе.

2. Построить машину Тьюринга, реализующую алгоритм .

3. Перевести из десятичной системы счисления в двоичную 119.

4. Каждый из учеников класса в зимние каникулы ровно два раза был в театре, при этом спектакли А, В и С видели соответственно 25, 12 и 23 ученика. Сколько учеников в классе? Сколько из них видели спектакли А и В, А и С, В и С?

5. Основные элементы графа. Способы задания графа (матрица инциденций)

6. Размещения, перестановка, сочетания.

7. Перевести из двоичной системы счисления в восьмеричную 11111111.

8. А – множество четных чисел x, ; В – множество делителей числа 21; С – множество простых чисел, меньших 12.

9. Определить, является ли функция монотонной?

f(x,y,z)=xyz

10. Определить, является ли функция линейной?

f(x,y)=(x y)

11. Является ли функция самодвойственной?

f(x,y)=(x y)

12. Полна ли система функций?

{xy, x 1}

13. Построить полином Жегалкина для функции:

f(x,y)=(x y)

14. Построить СДНФ для функции

f(x,y,z)=xyz

15. Построить СКНФ для функции

f(x,y,z)=xyz

16. Построить множество всех подмножеств P(M), если

M={a, {a,2},b}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(2,1),(2,3),(3,3),(4,3),(1,3), (3,1),(2,4),(1,2),(1,1)}

Вариант № 4

1. Шестеричная система счисления, операции в этой системе.

2. Построить машину Тьюринга, реализующую алгоритм

3. Перевести из десятичной системы счисления в двоичную 115.

4. В течение недели в кинотеатре демонстрировались фильмы А, В и С. Из 40 школьников, каждый из которых просмотрел либо все три фильма, либо один из трех, фильм А видели 13, фильм В – 16, фильм С – 19. Найти, сколько учеников просмотрели все три фильма.

5. Взвешенные графы, построение кратчайшего пути.

6. Задача Иосифа Флавия.

7. Перевести из двоичной системы счисления в восьмеричную 10101010.

8. Найти и зобразить эти множества на координатной прямой, если .

9. Определить, является ли функция монотонной?

f(x,y,z)=(xy

10. Определить, является ли функция линейной?

f(x,y)=(x y)

11. Является ли функция самодвойственной?

f(x,y)=(x y)

12. Полна ли система функций?

{x|y, x 1}

13. Построить полином Жегалкина для функции:

f(x,y)=(x y)

14. Построить СДНФ для функции

f(x,y,z)=(xy

15. Построить СКНФ для функции

f(x,y,z)=(xy

16. Построить множество всех подмножеств P(M), если

M={a, {1,2},2}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1)}

Вариант № 5

1. Восьмеричная система счисления, операции в этой системе.

2. Карта Карно.

3. Перевести из десятичной системы счисления в двоичную 117.

4. В отряде из 40 ребят 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого. Сколько ребят умеют плавать и играть в шахматы.

5. Число независимых циклов (Теорема Эйлера).

6. Задача о Ханойской башне.

7. Перевести из двоичной системы счисления в восьмеричную 10001110.

8. Найти и зобразить эти множества на координатной прямой, если .

9. Определить, является ли функция монотонной?

f(x,y)=(x y)(y )

10. Определить, является ли функция линейной?

f(x,y)=(xy

11. Является ли функция самодвойственной?

f(x,y)=(xy

12. Полна ли система функций?

{xy, x|1}

13. Построить полином Жегалкина для функции:

f(x,y)=(xy

14. Построить СДНФ для функции

f(x,y)=(x y)(y )

15. Построить СКНФ для функции

f(x,y)=(x y)(y )

16. Построить множество всех подмножеств P(M), если

M={2, {a,2},1}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(1,1),(2,2),(3,3),(4,4),(1,3),(3,1),(2,4),(4,2)}

Вариант № 6

1. Шестеричная система счисления, операции в этой системе.

2. Реализовать алгоритм Эвклида на машине Тьюринга.

3. Перевести из двоичной системы счисления в четверичную 1101110.

4. На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги А, В и С. Результаты опроса оказались таковы: книгу А читало 25 учащихся, книгу В – 22, книгу С – также 22. Книгу А или В читали 33 ученика, А или С – 32, В или С – 31; все три книги прочли 10 учащихся. Сколько учеников прочли только по одной книге? Сколько учеников прочли только по одной книге? Сколько учащихся не читали ни одной из этих трех книг?

5. Определение дерева. Число различных деревьев. Разборка дерева.

6. Методы решения рекуррентных соотношений.

7. Перевести из двоичной системы счисления в восьмеричную 1100.

8. Найти и зобразить эти множества на координатной прямой, если .

9. Определить, является ли функция монотонной?

f(x,y)=(x

10. Определить, является ли функция линейной?

f(x,y)=(xy

11. Является ли функция самодвойственной?

f(x,y)=(xy

12. Полна ли система функций?

{x , x 1}

13. Построить полином Жегалкина для функции:

f(x,y)=(xy

14. Построить СДНФ для функции

f(x,y)=(x

15. Построить СКНФ для функции

f(x,y)=(x

16. Построить множество всех подмножеств P(M), если

M={a, {a,b},2}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1)}

Вариант № 7

1. Переход из p – ичной системы счисления в q- ичную.

2. Реализовать алгоритм сложения на машине Тьюринга.

3. Перевести из двоичной системы счисления в четверичную 1111.

4. Среди абитуриентов, выдержавших приемные экзамены в вуз, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трем предметам – 4. Сколько абитуриентов получили хотя бы одну пятерку? Сколько среди них получивших только одну пятерку?

5. Определение дерева. Число различных деревьев. Разборка дерева.

6. Способы задания булевой функции.

7. Перевести из двоичной системы счисления в шестеричную 11000011.

8. В спортивном лагере 65 % ребят умеют играть в футбол, 70 % - в волейбол и 75 % - в баскетбол. Каково наименьшее число ребят, умеющих играть и в футбол, и в волейбол, и в баскетбол?

9. Определить, является ли функция монотонной?

f(x,y)=(x y)

10. Определить, является ли функция линейной?

f(x,y,z)=(xy

11. Является ли функция самодвойственной?

f(x,y,z)=(xy

12. Полна ли система функций?

{xy, x 1}

13. Построить полином Жегалкина для функции:

f(x,y,z)=(xy

14. Построить СДНФ для функции

f(x,y)=(x y)

15. Построить СКНФ для функции

f(x,y)=(x y)

16. Построить множество всех подмножеств P(M), если

M={a, {a,b},b}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1),(2,2)}

Вариант № 8

1. Диады, тетрады.

2. Построить машину Тьюринга, реализующую алгоритм .

3. Перевести из двоичной системы счисления в четверичную 100111.

4. Изобразить на координатной плоскости множество, координаты (x,y) точек которого удовлетворяют условию: .

5. Задача о раскраске графов.

6. Числа Фиббоначи

7. Перевести из двоичной системы счисления в шестеричную 111001101.

8. Множества А и В – подмножества основного множества R. Найти и изобразить эти множества на координатной прямой .

9. Определить, является ли функция монотонной?

f(x,y,z)=(xy

10. Определить, является ли функция линейной?

f(x,y,z)=(xy

11. Является ли функция самодвойственной?

f(x,y,z)=(xy

12. Полна ли система функций?

{x , x 1}

13. Построить полином Жегалкина для функции:

f(x,y,z)=(xy

14. Построить СДНФ для функции

f(x,y,z)=(xy

15. Построить СКНФ для функции

f(x,y,z)=(xy

16. Построить множество всех подмножеств P(M), если

M={a, {a,2},1}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(2,1),(2,3),(3,3),(4,3),(1,3),(2,4),(1,4),(1,1),(2,2)}

Вариант № 9

1. Запись положительных натуральных чисел в заданном формате

2. Построить машину Тьюринга для вычисления функции

Sign x = .

3. Перевести из двоичной системы счисления в четверичную 1100110.

4. Изобразить на координатной плоскости множество, координаты (x,y) точек которого удовлетворяют условию: .

5. Построение минимального потока в сети.

6. Код Грэя.

7. Перевести из двоичной системы счисления в шестеричную 1001100110.

8. Множества А и В – подмножества основного множества R. Найти и изобразить эти множества на координатной прямой .

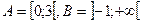9. Определить, является ли функция монотонной?

f(x,y,z)=(xy

10. Определить, является ли функция линейной?

f(x,y)=(x y)(y )

11. Является ли функция самодвойственной?

f(x,y)=(x y)(y )

12. Полна ли система функций?

{xy, x|y}

13. Построить полином Жегалкина для функции:

f(x,y)=(x y)(y )

14. Построить СДНФ для функции

f(x,y,z)=(xy

15. Построить СКНФ для функции

f(x,y,z)=(xy

16. Построить множество всех подмножеств P(M), если

M={1, {a,2},2}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(2,1),(2,3),(3,3),(4,3),(1,3),(3,2),(2,4),(1,4),(1,1)}

Вариант № 10

1. Планарные графы. Теорема.

2. О некоторых принципах кодирования информации.

3. Перевести из двоичной системы счисления в шестеричную 10010011.

4. Множества А и В – подмножества основного множества R. Найти и изобразить эти множества на координатной прямой .

5. Построение максимального потока в сети.

6. Числа подмножеств n – элементного множества.

7. Перевести из двоичной системы счисления в шестеричную 1001.

8. Множества А и В – подмножества основного множества R. Найти и изобразить эти множества на координатной прямой .

9. Определить, является ли функция монотонной?

f(x,y)=(xy

10. Определить, является ли функция линейной?

f(x,y,z)=xyz

11. Является ли функция самодвойственной?

f(x,y,z)=xyz

12. Полна ли система функций?

{xy, x x}

13. Построить полином Жегалкина для функции:

f(x,y,z)=xyz

14. Построить СДНФ для функции

f(x,y)=(xy

15. Построить СКНФ для функции

f(x,y)=(xy

16. Построить множество всех подмножеств P(M), если

M={a, {1,2},2}

17. Дать анкету для бинарного отношения, заданного ориентированным графом G=(V,A), V={1,2,3,4}

A={(1,2),(2,1),(1,3),(3,1),(2,3),(3,2),(2,4),(4,2)}

Список используемой литературы

1. Яблонский С. В. Введение в дискретную математику: Учебн. пособие для вузов./ Под ред. В. А. Садовничего. – 3-е изд., стер. – М.:Высш.шк..; 2001. – 384с.

2. Капитонова Ю. В. Лекции по дискретной математике / Авторы: Ю. В. Капитонова, С. Л. Кривой, А. А. Летичевский, Г. М. Луцкий / - СПб.: БХИ – Петербург, 2004. – 624с.: ил.

3. Дискретная математика для программистов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.: ил.

4. Донской В. И. Дискретная математика. – Симферополь: Издательство «СОНАТ», 2000. – 360 с. Илл. 45, библ. 17 назв.