Проверка аналитическим способом
Российский государственный университет
нефти и газа
им. И.М.Губкина
Кафедра нефтегазовой и подземной гидромеханики
Курсовая работа на тему
«Гидравлический расчет сложного трубопровода»
по курсу «Гидравлика»
К защите:
научный руководитель,
доцент
(подпись, дата)
студент группыРГ-08-6
(подпись, дата)
Защита:
Председатель комиссии
(подпись, дата)
Член комиссии
(подпись, дата)
Оценка
Москва,2010
Оглавление
Оглавление
§1 Оглавление. 2
§2 Задание на курсовую работу. 3
§3 Теоретическая часть. 4
§4 Расчетная часть. 8
§4.1 Задание №1. 8
§4.1 Задание №2. 12
§5 Выводы.. 15
§6 Проверка аналитическим способом. 16
§6.1 Задание №1. 16
§6.2 Задание №2. 18
§7 Заключение. 20
§8 Список литературы.. 21
Задание на курсовую работу
Кустовая насосная станция подает воду вязкостью v иплотностью ρ по коллектору длинной 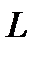 и диаметром
и диаметром 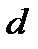 к трем скважинам. Длины и диаметры разводящих линий заданы. Расстояния от КНС до скважин заданы. Расстояние от КНС до первого разветвления
к трем скважинам. Длины и диаметры разводящих линий заданы. Расстояния от КНС до скважин заданы. Расстояние от КНС до первого разветвления 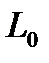 .
.
Задание №1
Определить расходы к скважинам и общий расход воды через KНС, если давления на КНС и устьях скважин заданы.
Задание №2
1) Определить, каким должно быть давление на КНС, чтобы расход увеличился в 1,2 раза;
2) Определить каким в этом случае будет расход к каждой скважине при условии, что давление на устьях осталось прежним.
Схема установки
| L1, d1 |
| КНС |
| L, d |
L 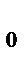 |
| L3, d3 |
| L2, d2 |
Исходные данные
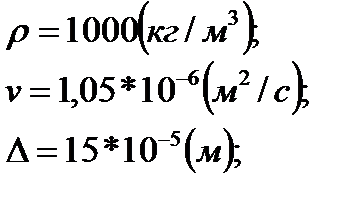
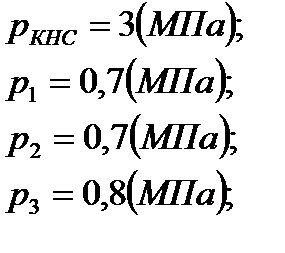
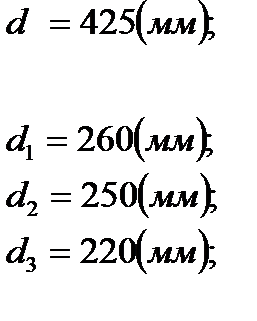
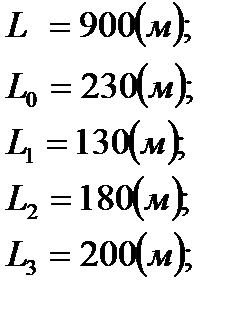
Теоретическая часть
Трубопроводы нашли широкое распространение во многих областях современной жизни, в том числе и в нефтегазовой отрасли. Поэтому диаметр, длина, шероховатость и другие параметры варьируются в широких пределах. Вследствие этого, существуют различные классификации трубопроводов. Учитывая специфику данной работы, рассмотрим деление на простые и сложные трубопроводы.
Простыминазывают трубопроводы одинакового по длине диаметра и состоящие из одной линии.
Сложными называют трубопроводы, в случае, если они имеют переменный по длине диаметр или имеют ветвления. Места трубопровода, где соединяется несколько ветвей, называют узлами.
При гидравлических расчетах сложного трубопровода может ставиться задача определения необходимого напора для обеспечения заданного расхода, либо определение расхода при заданных размерах и известных напорах. Исходными при этих расчетах являются уравнение Бернулли и уравнение сохранения расхода (или неразрывности).
Запишем уравнение Бернулли для некоторого участка трубопровода, расположенного между сечениями 1 и 2:
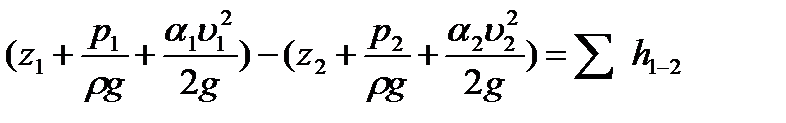 (1)
(1)
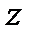 - геометрический напор;
- геометрический напор; 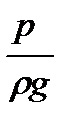 - пьезометрический напор;
- пьезометрический напор; 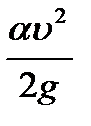 - скоростной напор;
- скоростной напор; 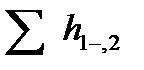 - потери напора на преодоление гидравлических сопротивлений.
- потери напора на преодоление гидравлических сопротивлений.
Причем:
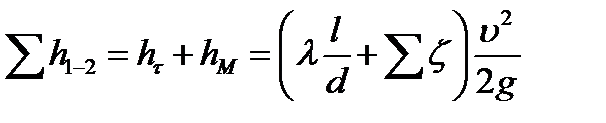 (2)
(2)
где 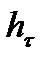 –потери напора по длине,
–потери напора по длине, 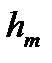 – местные потери напора на гидравлические сопротивления,
– местные потери напора на гидравлические сопротивления, 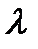 – коэффициент гидравлического сопротивления,
– коэффициент гидравлического сопротивления, 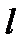 – длина трубопровода,
– длина трубопровода, 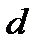 – диаметр трубопровода,
– диаметр трубопровода, 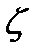 – коэффициент местного сопротивления,
– коэффициент местного сопротивления, 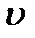 – скорость флюида,
– скорость флюида, 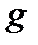 – ускорение свободного падения.
– ускорение свободного падения.
При решении данной курсовой работы, мы считаем, что:
1. Трубопровод лежит в одной горизонтальной плоскости:
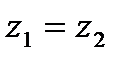 (3)
(3)
2. Местные потери напора пренебрежимо малы, по сравнению с потерями напора по длине. Тогда уравнение (2) примает вид:
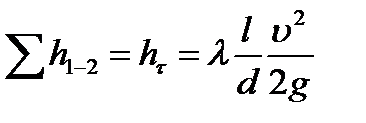 (4)
(4)
Уравнение (4) называется уравнением Дарси-Вейсбаха.
Также в данной курсовой работе участки, для которых записываются уравнения Бернулли, на всём протяжении имеют постоянный диаметр, поэтому 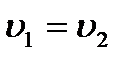 и
и 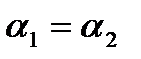 . Тогда уравнение (1) примает вид:
. Тогда уравнение (1) примает вид:
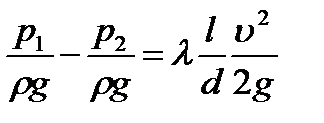 (5)
(5)
Средняя скорость жидкости, текущей по трубе определяется по формуле 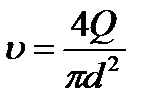 , подставляя это выражение в уравнение (4), получим:
, подставляя это выражение в уравнение (4), получим:
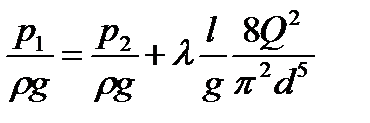 (6)
(6)
Коэффициент гидравлического сопротивления λ зависит от режима течения. В зависимости от значения Re, коэффициент гидравлического сопротивления определяется по различным формулам:
1. Ламинарный режим, Re<2320
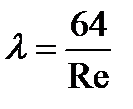 (7)
(7)
2. Турбулентный режим.
· Зона гидравлически гладких труб, 3000 ≤ Re ≤ 10d/∆.
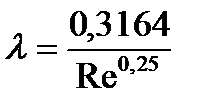 формула Блазиуса; (8)
формула Блазиуса; (8)
· Зона смешанного трения, 10d/∆ ≤ Re ≤ 500d/∆. (9)
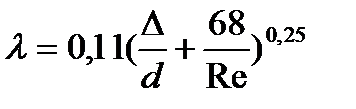 формула Альтшуля; (10)
формула Альтшуля; (10)
· Квадратичная зона, Re ≥ 500d/∆.
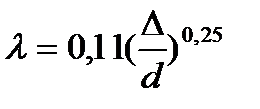 формула Шифринсона. (11)
формула Шифринсона. (11)
Сложные трубопроводы делятся на следующие группы:
· параллельные соединения, когда к основной магистрали подключены параллельно ей еще одна или несколько труб;
· последовательные соединения, в которых жидкость проходит по магистрали, состоящей из труб различного диаметра.
Параллельное соединение труб (рис.1). Магистральный трубопровод разветвляется на несколько параллельных линий труб различных длин и диаметров, сходящихся затем в точке магистрали. Если расход жидкости в магистрали 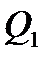 , а параллельных линиях
, а параллельных линиях 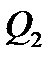 ,
, 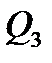 ,
, 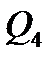 , то:
, то:
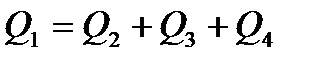 (12)
(12)
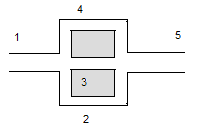 Рис.1
Рис.1
Составляя уравнение Бернулли для каждой из параллельных ветвей, получим, что потери напора равны между собой:
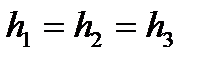 (13)
(13)
Последовательное соединение труб (рис.2). Магистральный трубопровод состоит из труб различной длины и диаметра. Если обозначить общий расход жидкости через 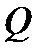 , то очевидно, что:
, то очевидно, что:
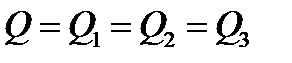 (14)
(14)
При этом потери напора определяются по формуле:
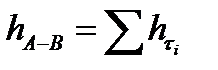 (15)
(15)
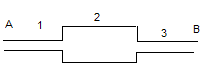 Рис.2
Рис.2
Независимо от того, какая задача нам поставлена при гидравлическом расчете сложного трубопровода, ее удобно решать графоаналитическим методом. Для этого строят гидравлические характеристики всех труб Н = f (Q), входящих в рассматриваемую схему. Характеристики параллельно соединенных труб суммируют согласно уравнениям (12) и (13). Для этого необходимо на графике сложить абсциссы (расходы) каждой из кривых при одинаковых ординатах (напорах). В результате такого суммирования получим характеристику разветвленного участка, которую можно рассматривать как заменяющую параллельно соединенные трубы одной им эквивалентной. Характеристики последовательно соединенных труб суммируют согласно уравнениям (14) и (15). Для этого необходимо на графике сложить напоры каждой из кривых при одинаковых расходах. В результате получим характеристику участка, которую можно рассматривать как заменяющую последовательно соединенные трубы одной им эквивалентной.
Расчетная часть
Задание №1
1) Введем новые буквенные обозначения на схеме установки и обозначим расходы жидкости на каждом участке трубопровода:
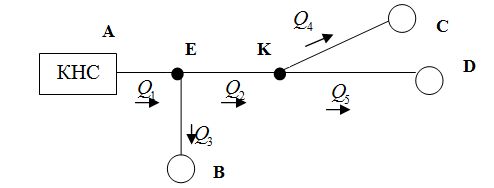
2) Задаем в программе Microsoft Excel расход жидкости для каждого участка трубопровода. Далее вычисляем для каждого значения расхода скорость жидкости и число Re. В зависимости от полученного значения числа Re, вычисляем коэффициент гидравлического сопротивления по одной из формул (7) – (11). В данной курсовой работе коэффициент гидравлического сопротивления λ рассчитывается по формуле Альтшуля и по формуле Шифринсона. После вычисления λ определяем потери напора по длине для каждого участка согласно формуле Дарси – Вейсбаха.
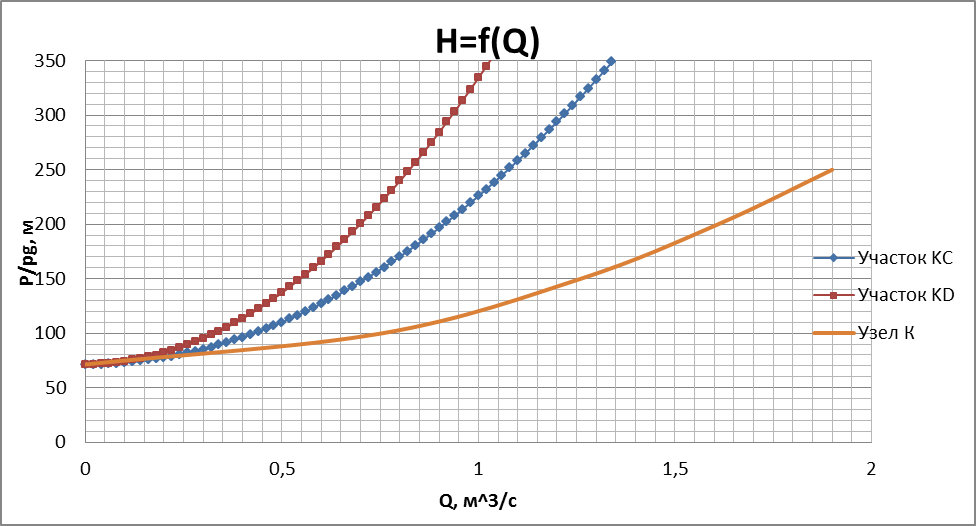
3) Так как нам известны давления на скважинах 1(С) и 2(D), можно построить график зависимости H=f(Q) для участков KC и KD по уравнениям:
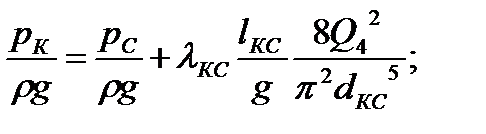
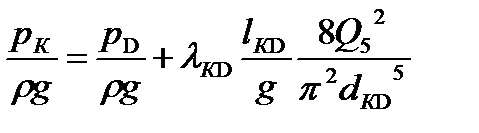
Так как участки KC и KD параллельны, то их общая характеристика строится в соответствии с уравнениями (12) и (13) (рис. 3).
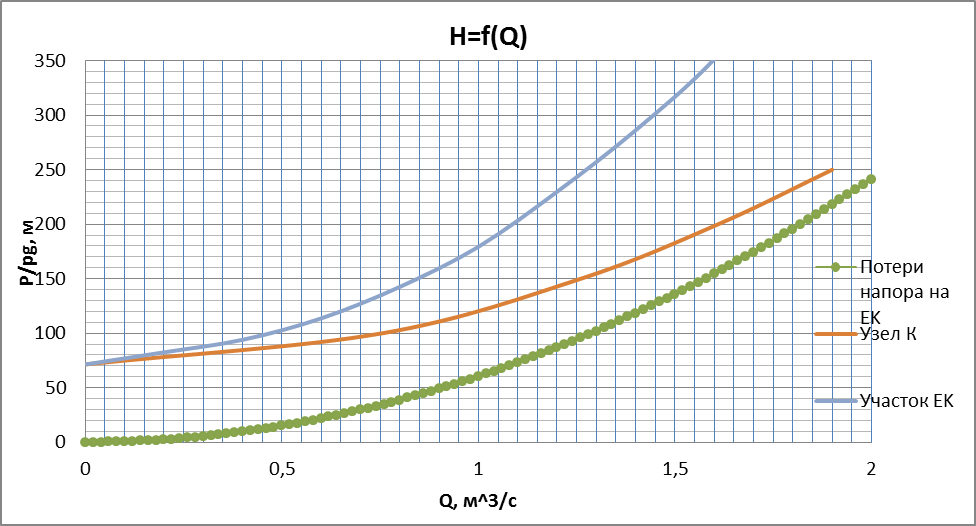
4) Рассмотрим участок EK. Построим график потерь напора для этого участка по уравнению:
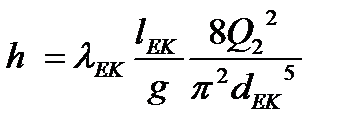
Для получения зависимости потерь напора от расхода на участке EK сложим кривую, отражающую потери напора по длине для участка EK и общую кривую из пункта 3) в соответствии с уравнениями (14) и (15) (рис. 4).
5) Построим график зависимости H=f(Q) для участка EB по уравнению:
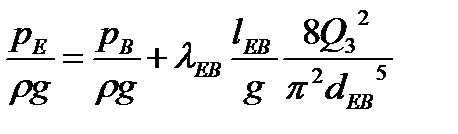
Сложим полученную кривую с кривой, полученной в пункте 4) в соответствии с уравнениями (12) и (13) (рис. 5).
6) Построим график зависимости H=f(Q) для участка AE (рис. 5) по уравнению:
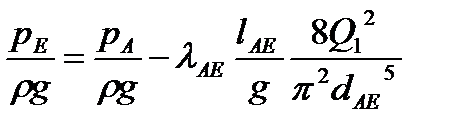
7) Точка пересечения кривых полученных в пункте 5) и 6) даст нам общий расход воды через КНС. Остальные расходы определяются по формулам (12) – (15).
| Рис. 3 |
| Рис. 4 |
| Рис. 5 |
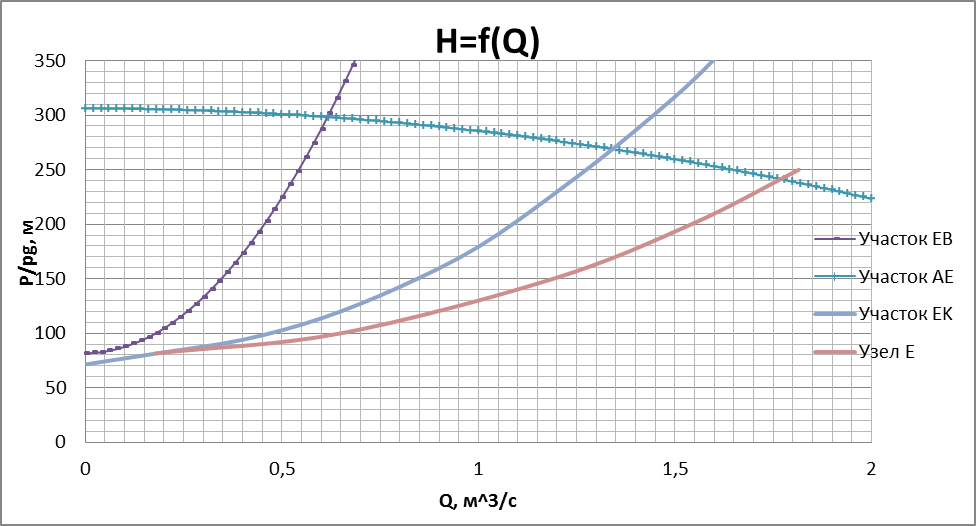
| Рис. 6 |
Задание №2
В этом задании исходные данные такие же, как и в первом задании, но теперь нам нужно найти давление на КНС и расходы к каждой скважине при известном расходе жидкости через КНС:
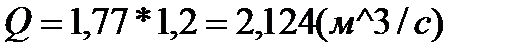
Ход работы аналогичен описанному в задании 1:
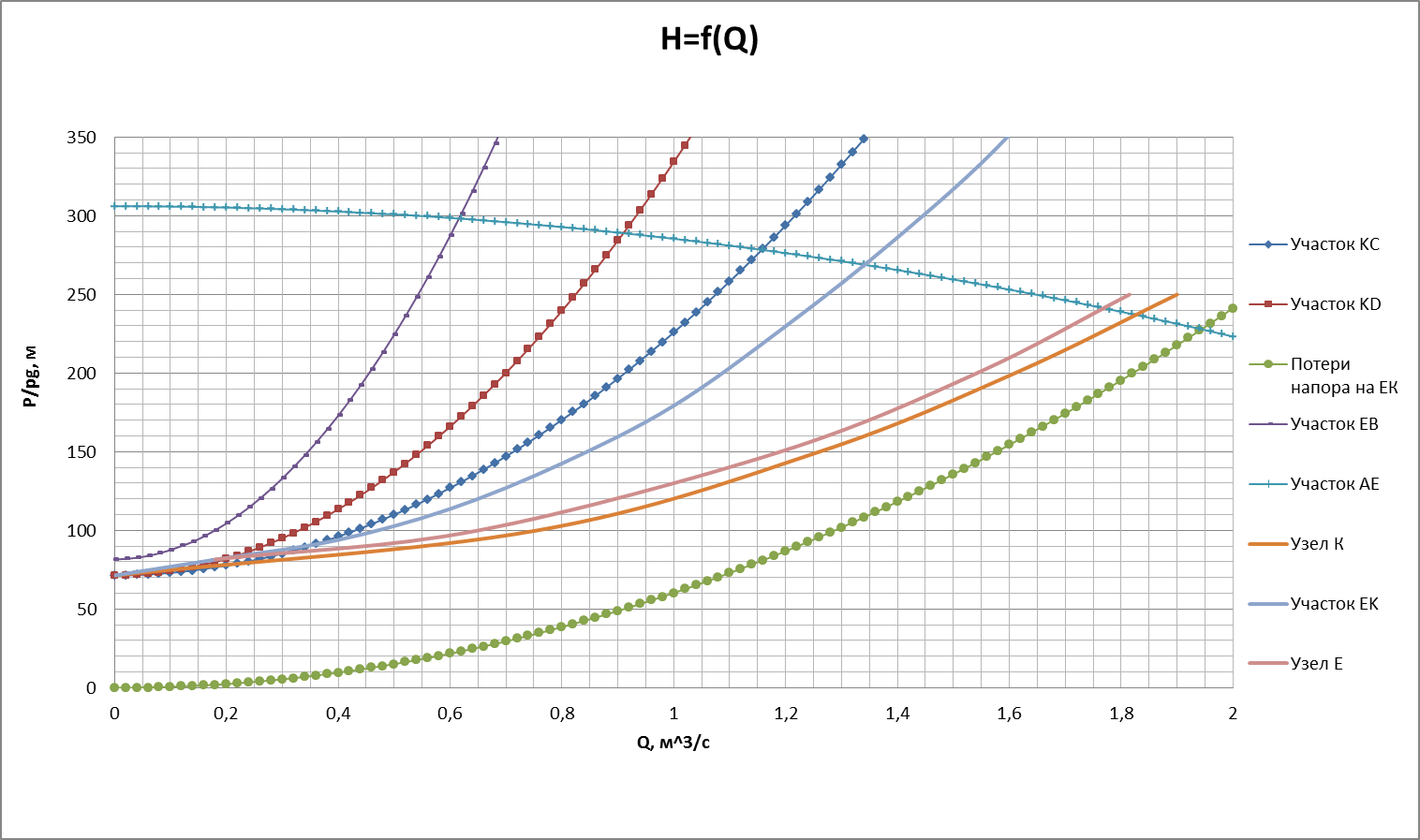
1) Построим график зависимости H=f(Q) для участков KC и KD и их общую характеристику (рис. 7);
2) Построим график потерь напора для этого участка EK и сложим эту кривую с общей кривой из пункта 1) (рис. 8);
3) Построим график зависимости H=f(Q) для участка EB и сложим полученную кривую с кривой, полученной в пункте 2) (рис. 9).
4) Так, как расход воды через КНС известен, можно определить потери напора по длине в трубе AE, а по кривой, полученной в пункте 3), можно определить напор при данном расходе. Подставив, полученные значения в формулу (5), определим давление на КНС.
5) По графику на рис. 10 определим расходы к каждой скважине.
| Рис. 7 |
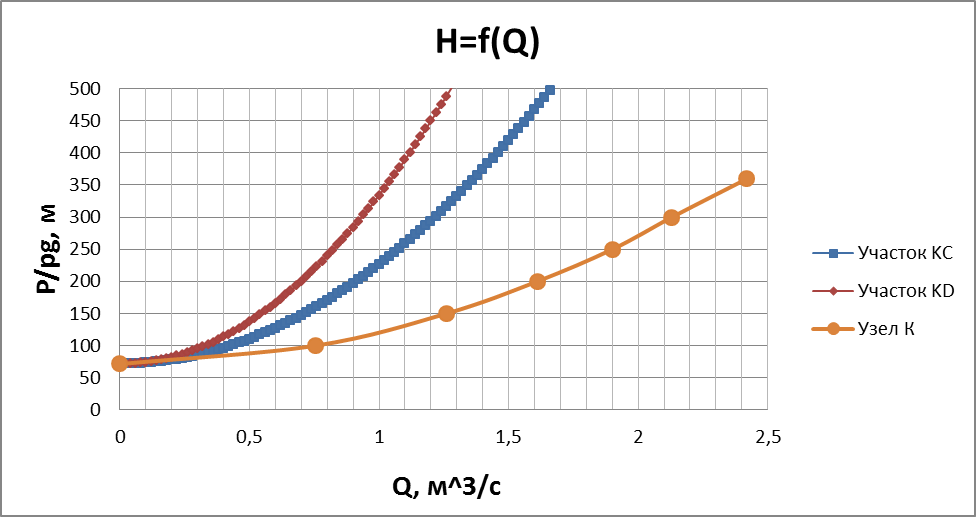
| Рис. 8 |
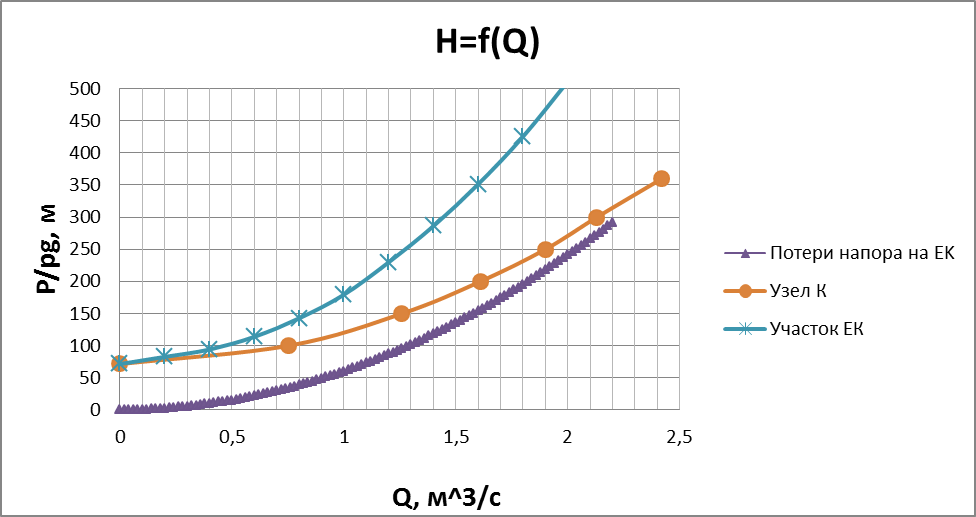
| Рис. 9 |
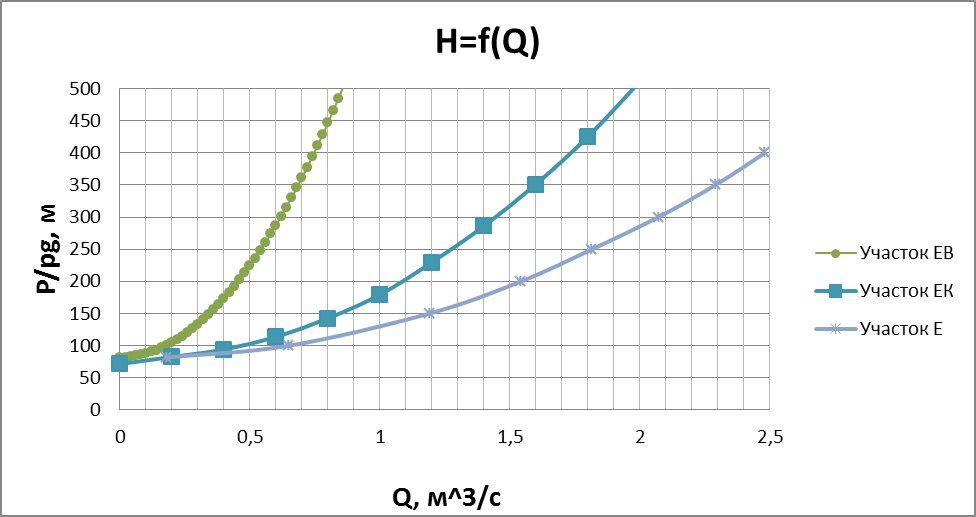
| Рис. 10 |
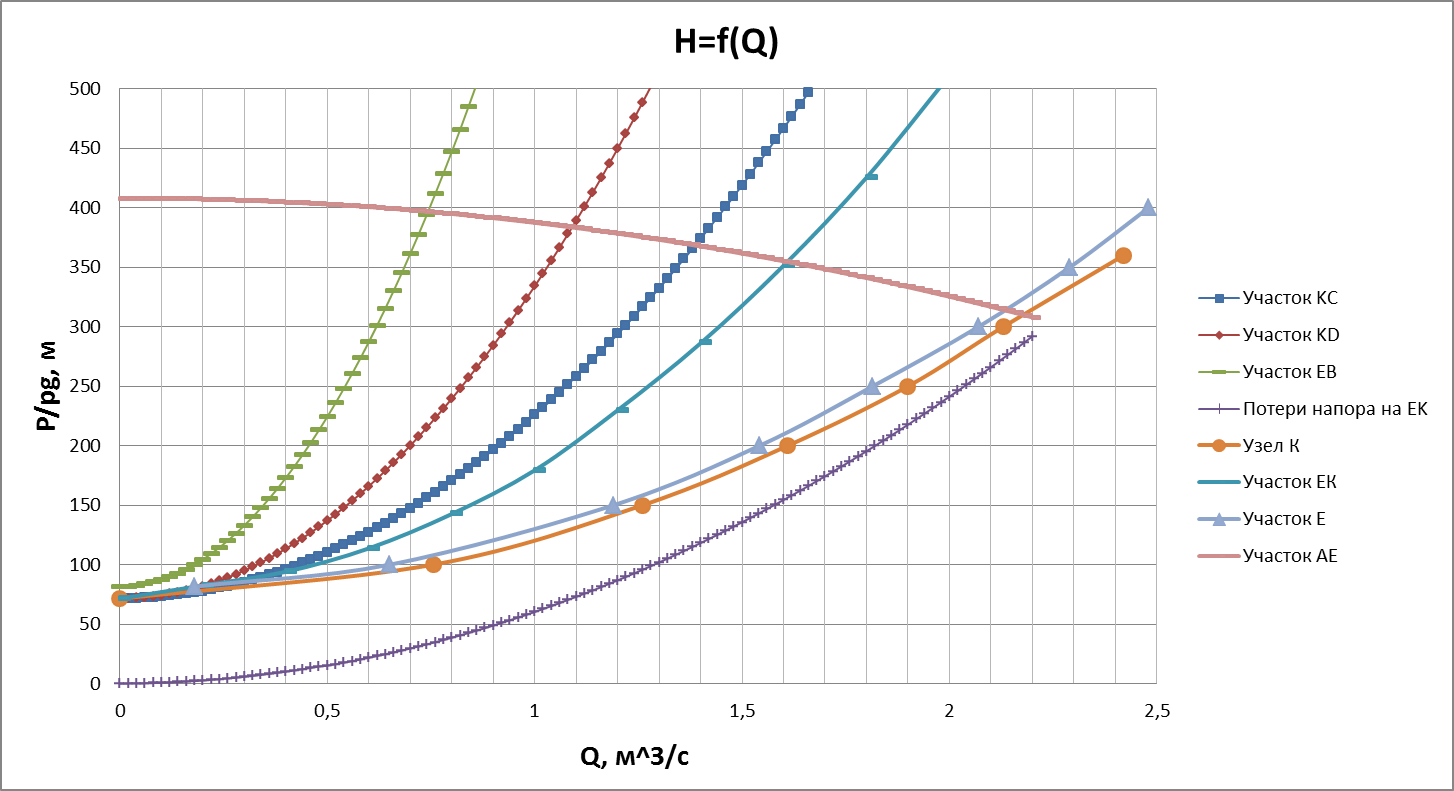
Выводы
Задание №1
На основании графика (рис.6), можно определить общий расход и расход жидкости к каждой скважине:
Q1=1,77 (м^3/c);
Q3=0,53(м^3/c);
Q4=0,7(м^3/c);
Q5=0,54(м^3/c).
Задание №2
По Рис.10 определяем давление на КНС и расходы каждой скважине:
Pкнс=3999184 (Па);
Q3=0,64(м^3/c);
Q4=0,84(м^3/c);
Q5=0,65(м^3/c).
Проверка аналитическим способом
Задачи по гидравлическому расчету сложного трубопровода можно решать аналитическим способом. Этот способ дает нам более точные результаты, чем графоаналитический. Однако, аналитически задача может быть решена в тех случаях, когда до начала расчета можно предсказать режим течения, а значит и вид зависимости λ от Re.
В данной работе зависимость λ от Re не была задана изначально. В ходе решения курсовой работы выяснилось, что коэффициент гидравлического сопротивления вычисляется по формуле Шифринсона, и только при малых значениях расхода - по формуле Альтшуля. Поэтому будем считать, что :
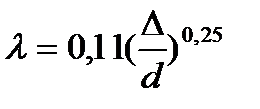

Задание №1
Для того, чтобы найти значения расходов воды к каждой скважине необходимо составить 2 уравнения сохранения расхода и 3 уравнения Бернулли:
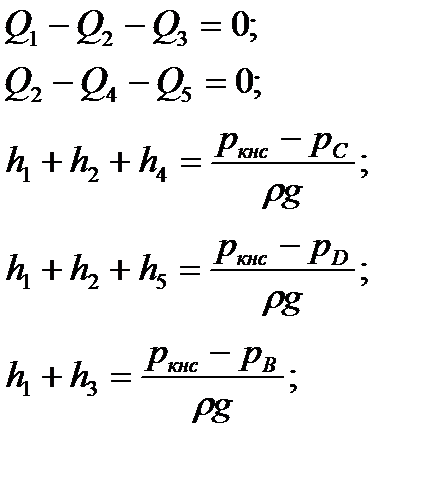 (16)
(16)
Если вместо hв систему уравнений (16) выразить через расход, то получится система из 5 уравнений с пятью неизвестными:
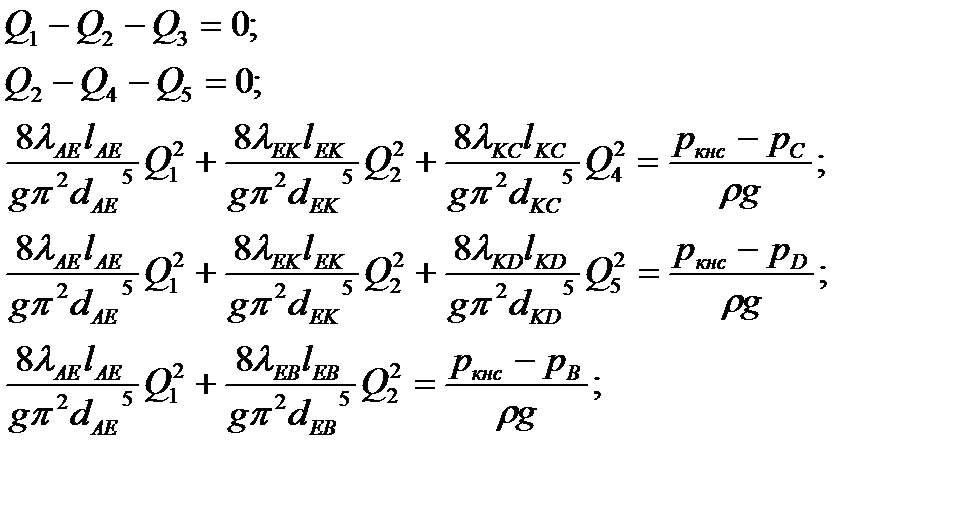 (17)
(17)
Ниже приведен текст программы в системе Matlab для решения системы уравнений (17) и нахождения расходов.
uc_1=[230 425e-003];
uc_2=[670 425e-003];
uc_3=[200 220e-003];
uc_4=[130 260e-003];
uc_5=[180 250e-003];
p_kns=3e+006;
p_b=0.8e+006;
p_c=0.7e+006;
p_d=0.7e+006;
lym_1=0.11*(0.00015/uc_1(1,2))^0.25
lym_2=0.11*(0.00015/uc_2(1,2))^0.25
lym_3=0.11*(0.00015/uc_3(1,2))^0.25
lym_4=0.11*(0.00015/uc_4(1,2))^0.25
lym_5=0.11*(0.00015/uc_5(1,2))^0.25
koaf_1=lym_1*uc_1(1,1)*8/(uc_1(1,2)^5*9.8*3.14^2)
koaf_2=lym_2*uc_2(1,1)*8/(uc_2(1,2)^5*9.8*3.14^2)
koaf_3=lym_3*uc_3(1,1)*8/(uc_3(1,2)^5*9.8*3.14^2)
koaf_4=lym_4*uc_4(1,1)*8/(uc_4(1,2)^5*9.8*3.14^2)
koaf_5=lym_5*uc_5(1,1)*8/(uc_5(1,2)^5*9.8*3.14^2)
function G = myfun( x )
G= [x(1) - x(2) - x(3) + 0*x(4) + 0*x(5);
0*x(1)+x(2)+0*x(3)-x(4)-x(5);
20.7065*x(1)*x(1)+60.3188*x(2)*x(2)+0*x(3)+154.4377*x(4)*x(4)+0*x(5)-(3000000-700000)/(1000*9.8);
20.7065*x(1)*x(1)+60.3188*x(2)*x(2)+0*x(3)+0*x(4)+262.7287*x(5)*x(5)-(3000000-700000)/(1000*9.8);
20.7065*x(1)*x(1)+0*x(2)+571.1248*x(3)*x(3)+0*x(4)+0*x(5)-(3000000-800000)/(1000*9.8)];
x0=[0.55;0.55;0.55;0.55;0.55];
options=optimset('Display','iter');
Q=fsolve(@myfun,x0,options)
После запуска программы на экране компьютера появятся значения расходов по всем участкам трубопровода с размерностью м^3/c:
Q1=1.7717
Q2=1.2432
Q3=0.5285
Q4=0.7037
Q5=0.5395
Задание №2
В первом задании надо было найти Q1, Q2, Q3, Q4, Q5 из (17) при заданных значениях давлений и др. характеристик. Во втором задании необходимо найти pкнс, Q2, Q3, Q4, Q5 при заданном расходе воды через КНС, тех же давлениях на скважинах и прочих других известных параметрах. Несмотря на то, что задача поменялась, система (17) по-прежнему состоит из пяти уравнений и пяти неизвестных, т.е. ее можно решить в системе Matlab:
uc_1=[230 425e-003];
uc_2=[670 425e-003];
uc_3=[200 220e-003];
uc_4=[130 260e-003];
uc_5=[180 250e-003];
p_b=0.8e+006;
p_c=0.7e+006;
p_d=0.7e+006;
lym_1=0.11*(0.00015/uc_1(1,2))^0.25
lym_2=0.11*(0.00015/uc_2(1,2))^0.25
lym_3=0.11*(0.00015/uc_3(1,2))^0.25
lym_4=0.11*(0.00015/uc_4(1,2))^0.25
lym_5=0.11*(0.00015/uc_5(1,2))^0.25
koaf_1=lym_1*uc_1(1,1)*8/(uc_1(1,2)^5*9.8*3.14^2)
koaf_2=lym_2*uc_2(1,1)*8/(uc_2(1,2)^5*9.8*3.14^2)
koaf_3=lym_3*uc_3(1,1)*8/(uc_3(1,2)^5*9.8*3.14^2)
koaf_4=lym_4*uc_4(1,1)*8/(uc_4(1,2)^5*9.8*3.14^2)
koaf_5=lym_5*uc_5(1,1)*8/(uc_5(1,2)^5*9.8*3.14^2)
function F = myfun1( y )
F= [y(1)*0 - y(2) - y(3) + 0*y(4) + 0*y(5)+2.126;
0*y(1)+y(2)+0*y(3)-y(4)-y(5);
(1/(1000*9.8))*(-1)*y(1)+60.3188*y(2)*y(2)+0*y(3)+154.4377*y(4)*y(4)+0*y(5)+ (700000/1000/9.8+20.7065*2.124^2);
(1/(1000*9.8))*(-1)*y(1)+60.3188*y(2)*y(2)+0*y(3)+0*y(4)+262.7287*y(5)*y(5)+ (700000/1000/9.8+20.7065*2.124^2);
(1/(1000*9.8))*(-1)*y(1)+0*y(2)+571.1248*y(3)*y(3)+0*y(4)+0*y(5)+ (800000/1000/9.8+20.7065*2.124^2)];
y0=[4000000;0.55;0.55;0.55;0.55];
options=optimset('Display','iter');
A=fsolve(@myfun1,y0,options)
Запустив эту программу получим значения давления на КНС c размерностья Па и расходов по всем участкам трубопровода с размерностью м^3/c :
p1= 3998357,5
Q2= 1,4876
Q3= 0,6384
Q4= 0,8420
Q5= 0,6456
Заключение
Сопоставим результаты полученные обоими способами:
графоаналитический аналитический
Задание №1
Q1=1,77 (м^3/c) Q1=1,7717 (м^3/c)
Q3=0,53(м^3/c) Q3=0,5285 (м^3/c)
Q4=0,7(м^3/c) Q4=0,7037 (м^3/c)
Q5=0,54(м^3/c) Q5=0,5395 (м^3/c)
Задание №2
Pкнс=3999184 (Па) Pкнс =3998357,5 (Па)
Q3=0,64 (м^3/c) Q3= 0,6384(м^3/c)
Q4=0,84 (м^3/c Q4= 0,8420 (м^3/c)
Q5=0,65 (м^3/c) Q5= 0,6456 (м^3/c)
Таким образом, мы видим, что результаты, полученные обоими методами практически не отличаются. При этом, аналитический способ дает нам более точные результаты, при меньших затратах времени на их вычисление. Однако, аналитический способ имеет серьезный недостаток, который заключается в том, что, если допустить незначительную ошибку на начальном этапе решения задачи, то могут получиться совершенно бессмысленные результаты ( расход отрицателен и т.д) или получить результаты похожие на правильные, но таковыми не являющимися. В то время как графоаналитический способ позволяет нам контролировать процесс решения задачи и во время исправлять какие-либо ошибки. Поэтому в заключении необходимо сказать о том, что нужно использовать одновременно оба метода при проведении расчетов.
Список литературы
1) «Гидравлика» Арустамова Ц.Т., Иванников В.Г., Москва, «Недра» 1995
2) «Прикладные задачи гидравлики» Разбегина Е.Г., Сумбатова А.Р., Москва, «Недра» 2007
