Тема №22.ДУ, допускающие понижение степени

В общем случае дифференциальное уравнение второго порядка можно записать в виде

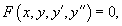
где F − заданная функция указанных аргументов.

Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:

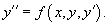
В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов:

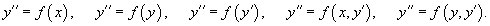
С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка.

В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):

• Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y'';
• Функция F(x, y, y', y'') является точной производной функции первого порядка

Ф(x, y, y')..

1. Уравнение вида y''= f (x)

Если дано уравнение y'' = f(x), то его порядок можно понизить введением новой функции p(x), такой, что y' = p(x). В результате мы получим дифференциальное уравнение первого порядка

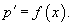
Решая его, находим функцию p(x). Затем решаем второе уравнение

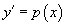
и получаем общее решение исходного уравнения.

2. Уравнение вида y''= f (y)

Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p(y), полагая y' = p(y). Тогда можно записать:

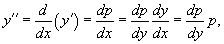
и уравнение принимает вид:

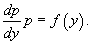
Решая его, находим функцию p(y). Затем находим решение уравнения y' = p(y), то есть функцию y(x).

3. Уравнение вида y''= f (y' )

В данном случае для понижения порядка вводим функцию y' = p(x) и получаем уравнение

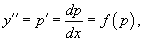
которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p(x) и затем функцию y(x).

4. Уравнение вида y''= f (x, y' )

Используем подстановку y' = p(x), где p(x) − новая неизвестная функция, и получаем уравнение первого порядка

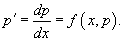
Интегрируя, определяем функцию p(x). Далее решаем еще одно уравнение 1-го порядка

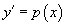
и находим общее решение y(x).

5. Уравнение вида y''= f (y,y' )

Для решения такого уравнения, также как и в случае 2, вводим новую функцию p(y), полагая y' = p(y). Дифференцирование этого равенства по x приводит к уравнению

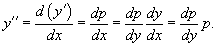
В результате наше исходное уравнение записывается в виде уравнения 1-го порядка

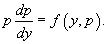
Решая его, находим функцию p(y). Затем решаем еще одно уравнение первого порядка

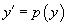
и определяем общее решение y(x).

1.Решить уравнение y'' = sin x + cos x.

Решение.

Данный пример относится к случаю 1. Введем функцию y' = p(x). Тогда y'' = p'. Следовательно,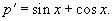

Интегрируя, находим функцию p(x):

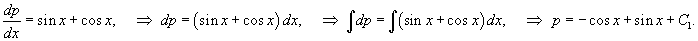
Учитывая, что y' = p(x), проинтегрируем еще одно уравнение 1-го порядка:

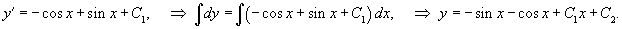
Последняя формула представляет собой общее решение исходного дифференциального уравнения.

2.Решить уравнение .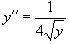

Решение.

Это уравнение относится к типу 2, где правая часть зависит лишь от переменной y. Введем параметр p = y'. Тогда уравнение можно записать в виде

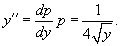
Мы получили уравнение 1-го порядка с разделяющимися переменными для функции p(y). Интегрируем его:

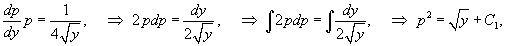
где C₁ − постоянная интегрирования.

Извлекая квадратный корень из обеих частей, находим функцию p(y):

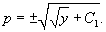
Теперь вспомним, что y' = p и решим еще одно уравнение 1-го порядка:

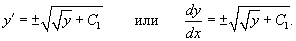
Разделим переменные и проинтегрируем:

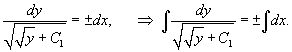
Чтобы вычислить левый интеграл, сделаем замену:

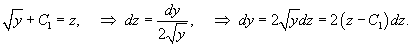
Тогда левый интеграл будет равен

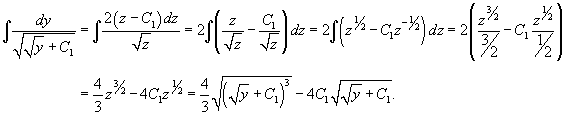
В результате мы получаем следующее алгебраическое уравнение:

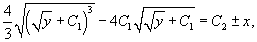
в котором C₁, C₂ являются постоянными интегрирования.

Последнее выражение представляет собой общее решение дифференциального уравнения в неявном виде.