Примеры выполнения заданий
Пример 1. Доказать тождество:
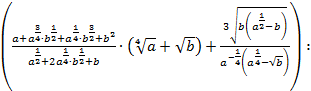
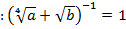
Решение. Для доказательства тождества выполним действия в левой части равенства:
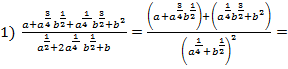
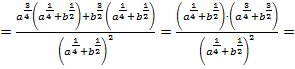
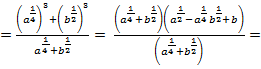
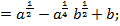
2) 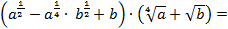
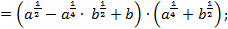
3) 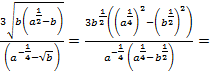
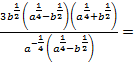
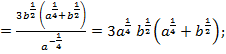
4) 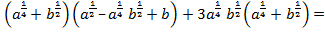
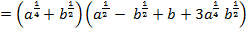 =
=
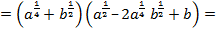
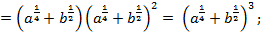
5) 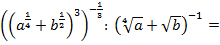
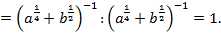
Левая часть выражения равна правой части: 1 = 1. Тождество доказано.
Замечание. При доказательстве тождеств, как правило, производится преобразование сразу всего выражения, а не по действиям.
Пример 2. Доказать тождество:
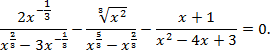
Доказательство:
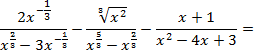
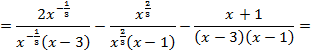
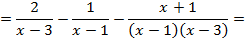
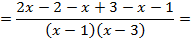
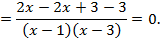
Левая часть выражения равна правой части: 0 = 0. Тождество доказано.
Пример 3. Доказать тождество:
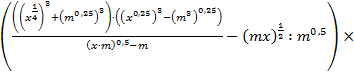
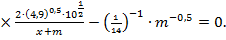
Доказательство:
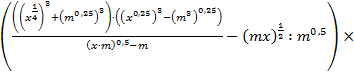
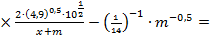
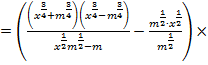
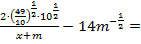
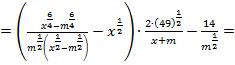
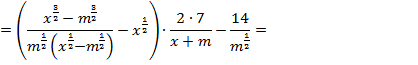
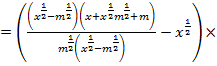
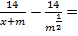
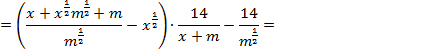
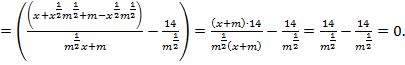
Левая часть выражения равна правой части: 0 = 0. Тождество доказано.
Пример 4. Найти значение выражения:
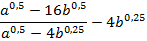
Если а = 16, b = 1.
Варианты ответов: 1) 6; 2) –2; 3) 4; 4) 2.
Решение. Преобразуем данное выражение, заметив, что в числителе дроби – разность квадратов:
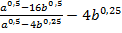
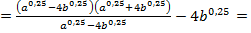
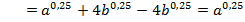
Вычислим значение при а = 16; 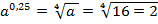 .
.
Ответ: правильный вариант ответа – четвертый.
Пример 5. Вычислить: 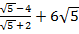 .
.
Решение. Приведем выражение к общему знаменателю и выполним действия:
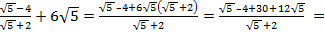
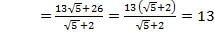 .
.
Ответ: 13.
Пример 6. Упростить 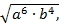 если
если 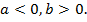
 Варианты ответов: 1)
Варианты ответов: 1) 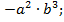 2)
2) 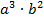 ; 3)
; 3) 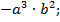 4)
4) 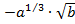 .
.
Решение. 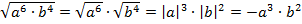 .
.
Ответ: правильный вариант ответа – третий.
Пример 7. Вычислить: 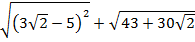 .
.
Решение. Поскольку 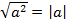 , то
, то
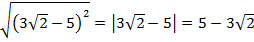 .
.
Кроме того, 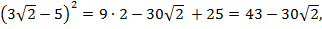 поэтому
поэтому 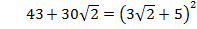 . Следовательно,
. Следовательно, 
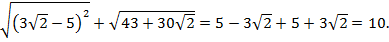
Ответ: 10.
Задачи для самостоятельного решения
1. Доказать тождества:
1) 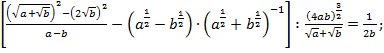
2) 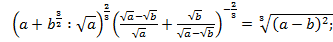
3) 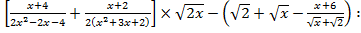
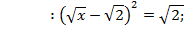
4) 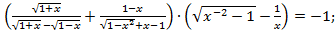
2. Найти значение выражения:
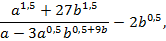
если а = 9, b = 16.
Варианты ответов: 1) 7; 2) 11; 3) 13; 4) 1.
Ответ: правильное значение – первое.
3. Упростите выражение: 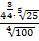 .
.
Варианты ответов: 1) 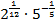 ; 2)
; 2) 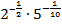 ; 3) 2
; 3) 2 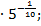
4) 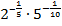
Ответ: правильное значение – третье.
4. Вычислить:
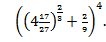
Ответ: 81.
Замечание. Следует иметь в виду, что 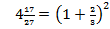 .
.
5. Найти значение выражения:
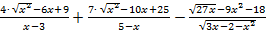 .
.
Ответ: 0.
РЕШЕНИЕ ЗАДАЧ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
Теоретические сведения
Задачи на составление уравнений, или текстовые задачи, условно разделяют на несколько типов: задачи на движение, задачи на совместную работу или планирование, задачи расчета и составления смесей, задачи на оптимальное решение и др. В настоящем разделе мы рассмотрим некоторые наиболее часто встречающиеся типы задач и методы их решения. В материалах Единого государственного экзамена по математике задачи на составление уравнений встречаются, как правило, в заданиях раздела Б. Несмотря на то, что задания указанного раздела не требуют развернутого ответа, основные этапы решения задачи (введение переменных, составление и решение уравнений) надо провести достаточно аккуратно, чтобы получить желаемый результат. Варианты традиционных экзаменов и олимпиад предполагают подробное решение задачи с указанием всех промежуточных выкладок.
