Геометрический смысл производной
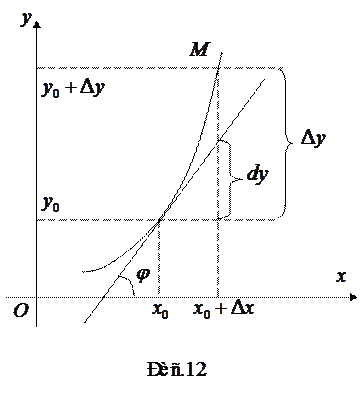 и дифференциала функции
и дифференциала функции
Пусть в декартовой прямоугольной системе координат задана кривая, являющаяся графиком функции 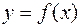 и на ней точка
и на ней точка 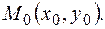 Производная
Производная 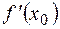 функции
функции 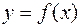 геометрически представляет собой угловой коэффициент касательной к графику функции в точке с абсциссой
геометрически представляет собой угловой коэффициент касательной к графику функции в точке с абсциссой 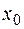 , т.е.
, т.е. 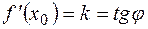 (см. рис.12). Тогда уравнение касательной к кривой
(см. рис.12). Тогда уравнение касательной к кривой 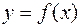 в точке
в точке  имеет вид:
имеет вид:
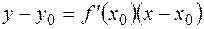
Дифференциал функции f(x)в точке 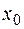 находится по формуле
находится по формуле 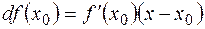 , т.е. равен произведению производной функции в заданной точке на дифференциал(приращение) независимой переменной. Геометрически дифференциал функции
, т.е. равен произведению производной функции в заданной точке на дифференциал(приращение) независимой переменной. Геометрически дифференциал функции 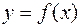 в точке
в точке 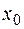 представляет собой приращение ординаты касательной к графику функции в точке
представляет собой приращение ординаты касательной к графику функции в точке 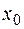 и при
и при 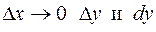 являются эквивалентными бесконечно малыми. Поэтому справедливо приближенное равенство
являются эквивалентными бесконечно малыми. Поэтому справедливо приближенное равенство 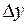 ~ dy, позволяющее приближенно заменять приращение функции дифференциалом.
~ dy, позволяющее приближенно заменять приращение функции дифференциалом.
ПРИМЕР 26.Найти координаты точки пересечения с осью Оу касательной к кривой 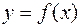 , где
, где  , проведенной к ней в точке
, проведенной к ней в точке 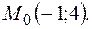
РЕШЕНИЕ:Уравнение касательной к кривой 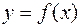 в точке
в точке 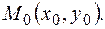 имеет вид
имеет вид 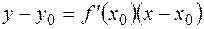 . Найдем сначала производную
. Найдем сначала производную 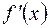 :
:
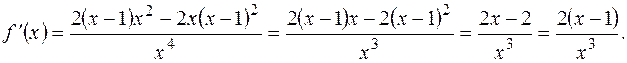
Вычислим 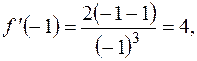 тогда уравнение касательной к заданной кривой в точке Мо(-1,4) запишется в виде:
тогда уравнение касательной к заданной кривой в точке Мо(-1,4) запишется в виде:
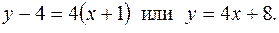
Теперь находим координаты точки пересечения полученной прямой с осью Оу.
Для всех точек, лежащих на оси Оу, х = 0. Подставим в уравнение касательной х = 0, получим у = 8. Значит, касательная у= 4х + 8 пересекает ось Оу в точке(0,8).
Применение правила Лопиталя к нахождению
Предела функции
При отыскании предела 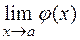 подстановка предельного значения
подстановка предельного значения 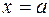 в ряде случаев приводит к неопределенным выражениям типа:
в ряде случаев приводит к неопределенным выражениям типа: 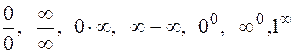 . Тогда вычисление заданного предела называют раскрытием неопределенности соответствующего типа. Обычно при этом используют правило Лопиталя.
. Тогда вычисление заданного предела называют раскрытием неопределенности соответствующего типа. Обычно при этом используют правило Лопиталя.
Раскрытие неопределенностей типа  и
и 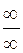
Непосредственно применять правило Лопиталя можно только для раскрытия неопределенностей типа  или
или 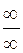 . Согласно этому правилу, предел отношения двух бесконечно малых (или двух бесконечно больших) существует и равен пределу отношения их производных:
. Согласно этому правилу, предел отношения двух бесконечно малых (или двух бесконечно больших) существует и равен пределу отношения их производных:
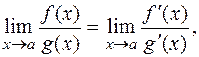
если выполнены условия:
1) функции f(x), g(x) дифференцируемы в некоторой окрестности точки х = а и g'(х) ≠ 0 в этой окрестности (кроме, может быть самой точки а);
2) 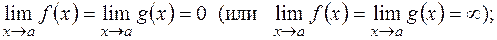
3) существует 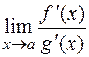 (конечный или бесконечный), при этом а может быть как числом, так и одним из символов:
(конечный или бесконечный), при этом а может быть как числом, так и одним из символов: 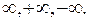
ПРИМЕР 28.Найти 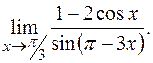
РЕШЕНИЕ:Поскольку 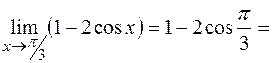
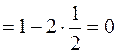 и
и 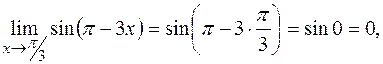 то имеем неопределенность типа
то имеем неопределенность типа  . Функции
. Функции  дифференцируемы на всей числовой оси. Найдем предел отношения их производных:
дифференцируемы на всей числовой оси. Найдем предел отношения их производных:
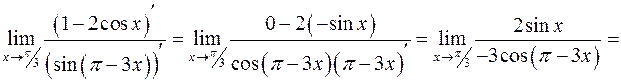
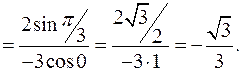
Так как этот предел существует, то согласно правилу Лопиталя:
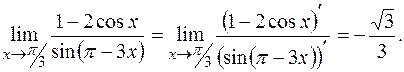
Замечание. Если предел отношения производных 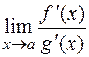 вновь представляет собой неопределенность типа
вновь представляет собой неопределенность типа  или
или 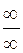 , то правило Лопиталя применяется еще раз.
, то правило Лопиталя применяется еще раз.
Раскрытие неопределенностей типа 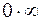 и
и 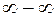
Неопределенность типа 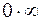 или
или 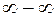 следует вначале путем тождественных преобразований привести к неопределенностям типа
следует вначале путем тождественных преобразований привести к неопределенностям типа  или
или 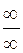 , для раскрытия которых можно непосредственно применить правило Лопиталя.
, для раскрытия которых можно непосредственно применить правило Лопиталя.
ПРИМЕР 29.Найти 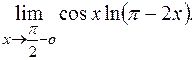
РЕШЕНИЕ: При 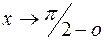 аргумент логарифмической функции
аргумент логарифмической функции 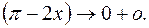 Так как
Так как 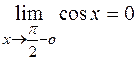 и
и 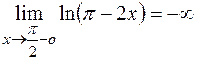 , то возникает неопределенность типа
, то возникает неопределенность типа 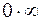 . Обычно в таких случаях один из сомножителей записывают в знаменатель данного выражения:
. Обычно в таких случаях один из сомножителей записывают в знаменатель данного выражения:
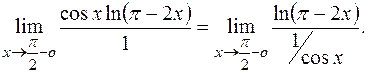
Получена неопределенность типа 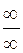 , к которой применимо правило Лопиталя:
, к которой применимо правило Лопиталя:
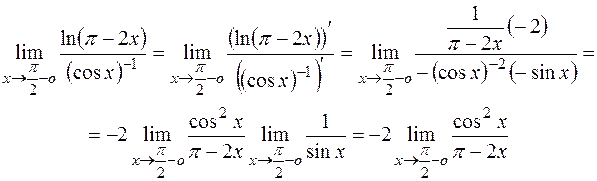
(поскольку 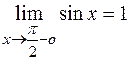 ). Здесь имеет место неопределенность типа
). Здесь имеет место неопределенность типа  , для раскрытия которой снова применяем правило Лопиталя:
, для раскрытия которой снова применяем правило Лопиталя:
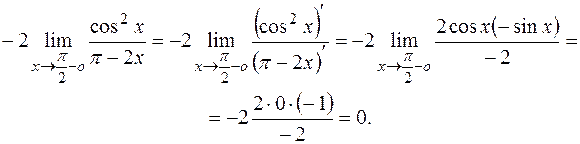
ПРИМЕР 30. Найти 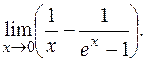
РЕШЕНИЕ: Выражение в скобках, представляющее собой неопределенность типа 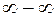 , приводим к общему знаменателю:
, приводим к общему знаменателю:
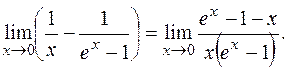
Полученную неопределенность типа  раскроем по правилу Лопиталя (в ходе вычислений это правило применено дважды):
раскроем по правилу Лопиталя (в ходе вычислений это правило применено дважды):
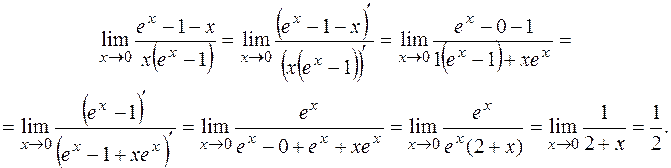
Раскрытие неопределенностей типа 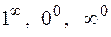

При раскрытии указанных неопределенностей используются:
а) основное логарифмическое тождество 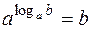 (в частности,
(в частности, 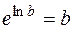 );
);
б) непрерывность показательной функции, в силу чего:
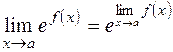
ПРИМЕР 31.Найти 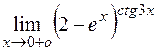 .
.
РЕШЕНИЕ:Поскольку 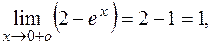
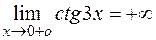 , имеем неопределенность типа
, имеем неопределенность типа 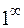 . Найдем вначале предел логарифма заданной функции:
. Найдем вначале предел логарифма заданной функции: 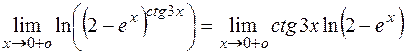 . Здесь возникла неопределенность типа
. Здесь возникла неопределенность типа 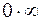 . Если учесть, что
. Если учесть, что 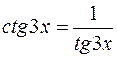 , то перейдем к неопределенности типа
, то перейдем к неопределенности типа  , которую можно раскрыть по правилу Лопиталя:
, которую можно раскрыть по правилу Лопиталя:
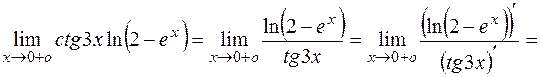
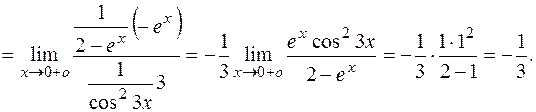
Теперь используем основное логарифмическое тождество и свойство непрерывности показательной функции:
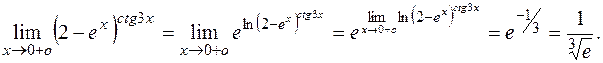
Таким образом, для вычисления  в случае неопределенностей
в случае неопределенностей 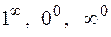 , применяем правило:
, применяем правило: 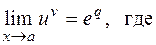
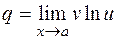 .
.
