Прямая линия на плоскости

1.1. Уравнение линии на плоскости.

Положение точки на плоскости определяется двумя координатами.

Прямоугольная декартова система координат на плоскости представляет из себя две перпендикулярные прямые, снабженные масштабами и направлениями. Такие прямые называются координатными осями - осью абсцисс Ох и осью ординат Оy.

Пусть на плоскости заданы декартова прямоугольная система координат и некоторая линия L. Рассмотрим уравнение F(x,y)=0 (или y=j(x)), связывающее две переменные величины x и y. Это уравнение называется уравнением линии L (относительно заданной системы координат), если 1) ему удовлетворяют координаты (x,y) любой точки линии L и 2) ему не удовлетворяют координаты ни одной точки, не лежащей на линии L.

1.2. Различные виды уравнения прямой.

В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени

Ax + By + C = 0 (1)

(где А и В не равны нулю одновременно) определяет некоторую прямую. Это уравнение называется общим уравнением прямой. Возможны следующие случаи:

1) С = 0, уравнение имеет вид Ax + By = 0 и определяет прямую, проходящую через начало координат;

2) В = 0 (А ¹ 0), уравнение принимает вид Ax + C = 0 или x = 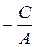- прямая, параллельная оси Oy (в частности, x = 0 - уравнение самой оси Oy);

3) А = 0 (В ¹ 0), уравнение принимает вид Вy + C = 0 или y = 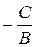- прямая, параллельная оси Ox (в частности, y = 0 - уравнение самой оси Ox).

M

y

y

Рис.1

Замечание. Для построения прямой, заданной общим уравнением, достаточно указать любые две ее точки.

N

Пример 1. Определить точки пересечения прямой 3x - 4y + 12= 0 с координатными осями и построить эту прямую.

-4

x

Решение. Полагая x = 0, находим y = 3; таким образом, получена точка М(0,3) пересечения

прямой с осью Oy. При y = 0 значение x = -4 и N(-4,0) - точка пересечения прямой с осью Ox. Осталось провести прямую через точки М и N (рис. 1). ■

Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду

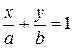, (2)

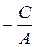где a = и b = 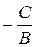есть величины отрезков, которые отсекает прямая на координатных осях. Уравнение (2) называется уравнением прямой «в отрезках». Эта форма уравнения прямой особенно удобна для построения прямой на чертеже. Так, в предыдущем примере, после записи уравнения прямой в виде 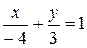, легко определить координаты точек М и N.

Рассмотрим на плоскости xOy прямую, не параллельную оси Oy; при движении вдоль такой прямой в одном направлении x возрастает, а в другом убывает. Направление, отвечающее возрастанию x, назовем положительным. Угол a, на который надо повернуть положительную полуось Оx, чтобы совместить ее с положительным направлением данной прямой, называют углом наклона прямой к оси абсцисс. При этом угол наклона считается положительным, если положительную полуось Оx надо поворачивать против часовой стрелки, и отрицательным в противном случае, так что 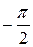< a < 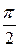. Можно считать, что для прямой, параллельной оси Оy, угол наклона a = .

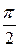Угловым коэффициентом прямой k называется тангенс угла наклона прямой к оси Оx:

k = .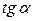

Замечание. Прямая, параллельная оси Оy, не имеет углового коэффициента, т.к. 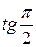не существует; или можно считать, что ее угловой коэффициент равен бесконечности, т.к. при a ® ® ¥.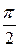

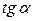Если прямая не параллельна оси Оy, то ее уравнение можно записать в виде

y = kx+b. (3)

Это уравнение называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент; b - величина отрезка, который отсекает прямая на оси Оy, считая от начала координат. В частном случае, при b = 0 прямая y = kx проходит через начало координат.

Из общего уравнения прямой (1) при В¹0 можно получить уравнение y = 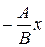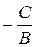, т.е. уравнение прямой с угловым коэффициентом k = .

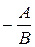Пример 2. Найти угол наклона к оси Оx прямой, заданной общим уравнением 2x + 5y + 17= 0.

Решение. Выразим из данного уравнения y. Получим уравнение прямой с угловым коэффициентом y = 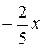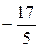. Откуда, k = 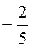= -0,4, так что 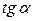= -0,4. Искомый угол a = . ■

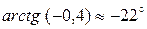Рассмотрим далее решение некоторых типовых задач.