Коэффициент гидравлического сопротивления
Если ввести в рассмотрение среднюю по сечению скорость 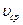 течения жидкости и обобщенное число
течения жидкости и обобщенное число 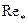 согласно равенствам
согласно равенствам
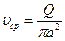 и
и 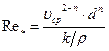 (11.16)
(11.16)
где 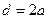 , то выражение (11.15) можно записать в привычной форме закона Дарси-Вейсбаха
, то выражение (11.15) можно записать в привычной форме закона Дарси-Вейсбаха
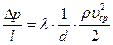 ,
,
т.е. через коэффициент 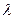 гидравлического сопротивления, где
гидравлического сопротивления, где
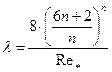 . (11.17)
. (11.17)
И так же при 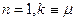 формула (11.17) переходит в ранее полученную формулу (7.28) Стокса.
формула (11.17) переходит в ранее полученную формулу (7.28) Стокса.
Пример 1. Найти перепад давлений, необходимый для перекачки высоковязкой парафинистой нефти с расходом 20 м3/ч, приняв для ее описания модель степенной неньютоновской жидкости с индексом 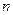 , равным 3/4. Известно, что при скорости
, равным 3/4. Известно, что при скорости 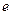 сдвига, равной
сдвига, равной 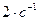 касательное напряжение
касательное напряжение 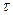 составляет 9,81 Н/м2. Диаметр трубопровода 0,2 м, его длина – 1000 м.
составляет 9,81 Н/м2. Диаметр трубопровода 0,2 м, его длина – 1000 м.
Решение. Поскольку 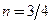 , то касательное напряжение и градиент скорости, связаны равенством
, то касательное напряжение и градиент скорости, связаны равенством
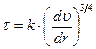 .
.
Поскольку при 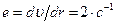 ,
, 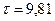 Н/м2, то
Н/м2, то
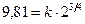 ,
,
откуда находится консистентность жидкости 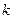 :
:
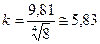 .
.
Для определения необходимого перепада давлений используем уравнение (11.14), разрешив его относительно 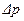 :
:
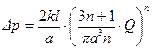 .
.
Подставив сюда численные значения параметров, получим:
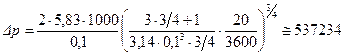 Н/м2
Н/м2
Ответ: 537234 Па ( 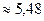 ат.).
ат.).
Для определения реологических свойств нефти и нефтепродуктов часто используют специальные приборы, называемые вискозиметрами. Наиболее распространенными являются капиллярные вискозиметры. Принцип действия всех капиллярных вискозиметров основан на определении времени свободного истечения фиксированной порции испытуемой жидкости из камеры прибора через узкую вертикальную цилиндрическую трубку (капилляр). Это время рассчитывается на основе формул (11.12) или (11.15) с заменой в них градиента давления 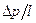 произведением
произведением 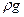 где
где 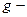 ускорение силы тяжести. Например, для рассматриваемой степенной жидкости расход
ускорение силы тяжести. Например, для рассматриваемой степенной жидкости расход 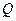 течения жидкости в вертикальном капилляре вискозиметра имеет вид:
течения жидкости в вертикальном капилляре вискозиметра имеет вид:
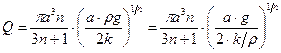 . (11.18)
. (11.18)
Пример 2. Для выявления свойств нефти проводят эксперименты по свободному истечению порции нефти объемом 100 мл из камеры вискозиметра. В первом опыте истечение происходит через цилиндрический капилляр с внутренним радиусом 1 мм, а во втором - через аналогичный капилляр с внутренним радиусом 1,5 мм. В первом опыте время истечения оказалось равным 1000 с, во втором - 180 с. Моделируя свойства нефти свойствами степенной жидкости, найти индекс 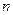 и кинематическую косистентность
и кинематическую косистентность 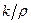 .
.
Решение. Из формулы (11.18) следует, что 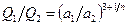 . Поскольку отношение расходов истечения обратно пропорционально временам истечения, то для расчета индекса
. Поскольку отношение расходов истечения обратно пропорционально временам истечения, то для расчета индекса 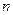 имеем уравнение:
имеем уравнение: 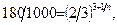 из которого находим:
из которого находим: 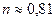 .
.
Используя результаты первого эксперимента, получаем уравнение:
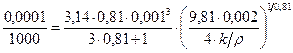 ,
,
из которого находим: 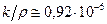 м2/с1,19.
м2/с1,19.
