Порядок выполнения работы. ЛАБОРАТОРНАЯ РАБОТА № 2.14

ЛАБОРАТОРНАЯ РАБОТА № 2.14

«ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЁМКОСТИ КОНДЕНСАТОРА С ПОМОЩЬЮ

БАЛЛИСТИЧЕСКОГО ГАЛЬВАНОМЕТРА»

Цель работы: экспериментальное определение динамической постоянной баллистического гальванометра и ёмкости конденсатора.

Описание электрической схемы

Электрическая схема, используемая в настоящей лабораторной работе, представлена на рис. 1. Здесь G – гальванометр баллистический, С – конденсатор, П – переключатель, V – вольтметр, Б – батарея ЭДС.

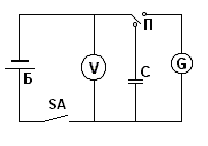
Рис. 1. Принципиальная схема установки

Когда переключатель П установлен в левое положение, происходит заряд конденсатора от батареи Б и одновременно гальванометр шунтируется критическим сопротивлением (не указанным в схеме). Благодаря этому рамка его устанавливается в положение равновесия. Когда переключатель П установлен в правое положение, конденсатор разряжается через гальванометр.

Пояснения к работе

Баллистический гальванометр предназначен для измерения количества электричества, протекающего через его рамку за время, значительно меньше периода её собственных колебаний. Баллистический гальванометр отличается от обычного гальванометра магнитоэлектрической системы тем, что подвижная часть его делается более массивной и обладает большим моментом инерции j.

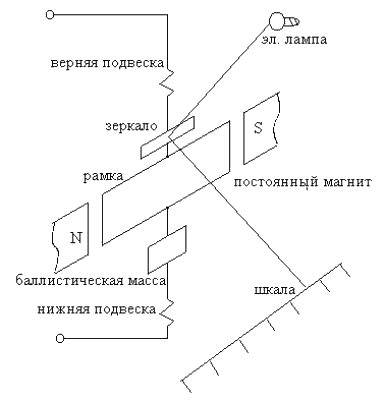
Рис. 2. Устройство гальванометра баллистического гальванометра.

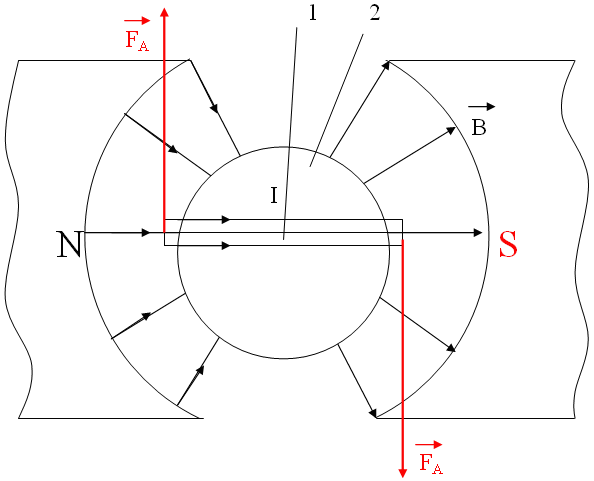
Рис. 3. Схема устройства баллистического гальванометра (вид сверху).

Проволочная рамка 1 и цилиндр из мягкого железа 2 подвешены на металлической нити в кольцевом зазоре между полюсами постоянного магнита N и S. Нить снабжена зеркальцем. Для измерения отклонения рамки от положения равновесия используется луч света, который направляется от лампочки на зеркальце и, отразившись от него, попадает на шкалу.

При кратковременном протекании тока J на рамку 1 со стороны внешнего магнитного поля 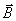действует пара сил Ампера 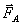, создающая вращающий момент.

Длительность импульса тока t много меньше периода собственных колебаний рамки Т (t << Т), т.к. подвижная часть гальванометра имеет большой момент инерции (из-за цилиндра 2). Поэтому воздействие на рамку момента сил Ампера имеет характер "удара" (отсюда название гальванометра).

При повороте рамки ее кинетическая энергия переходит в потенциальную энергию закрученной нити. Вместе с рамкой на угол a₀ поворачивается и зеркало (световой луч смещается на угол 2a₀). (рис. 3)

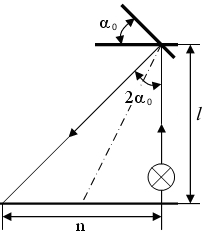
По линейной шкале измеряют смещение ("отскок") светового "зайчика", отраженного от зеркала. Заряд q, прошедший по рамке за время протекания тока, прямо пропорционален числу деления шкалы n: q=b × n где b - баллистическая постоянная гальванометра (зависит от целого ряда параметров прибора).

Рис. 3.

Движение рамки баллистического гальванометра описывается тем же уравнением, что и в случае обычного гальванометра магнитоэлектрической системы:

J 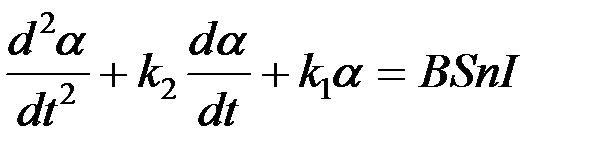, (1)

где К₁ – коэффициент крутильной упругости; К₂ – коэффициент электромагнитного торможения; В – модуль магнитной индукции; S – площадь рамки; n – нормаль к контуру.

Так как момент инерции j велик, в левой части уравнения (1) можно пренебречь вторым и третьим членами по сравнению с первым:

j 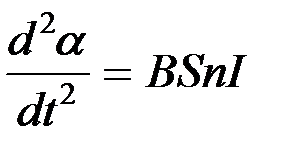. (2)

Количество электричества q, прошедшее через рамку за время t, можно определить, интегрируя уравнение (2):

j 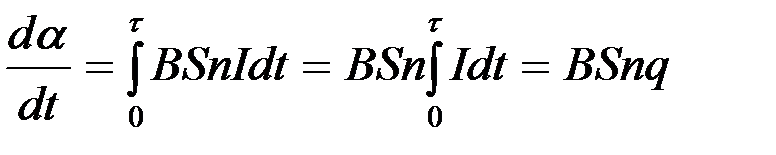. (3)

Кинетическая энергия рамки гальванометра равна

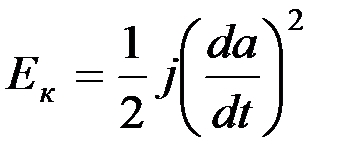(4)

которая переходит в потенциальную энергию закручивающейся на угол α нити:

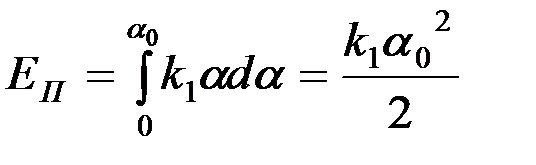. (5)

Момент инерции может быть определён из формулы для периода Т₀ упругих крутильных колебаний:

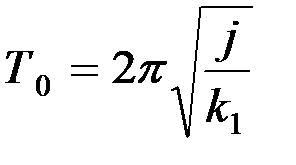(6)

Подставив формулы (4)-(6) в (3) и учитывая, что Е_К=Е_П, имеем

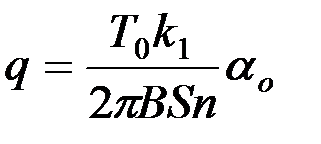, (7)

где

Обозначим 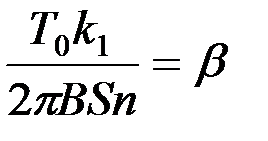. Из выражения (7) видно, что максимальный поворот рамки баллистического гальванометра пропорционален количеству протёкшего через него электричества:

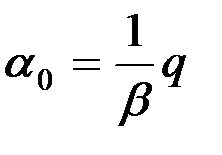, (8)

где величина β – динамическая постоянная гальванометра. Она определяет количество электричества, при протекании которого через рамку последняя повернётся на угол, равный 1 радиану.

Угол отклонения "зайчика" равен

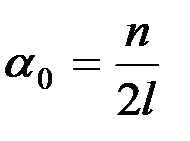, (9)

где n – отклонение светового «зайчика» по шкале;

l – расстояние от зеркала до шкалы.

Подставляя значение q из формулы для ёмкости конденсатора в формулу (8) и учитывая выражение (9), получим:

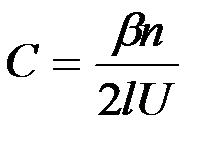. (10)

Порядок выполнения работы

Упражнение 1: Определение динамической постоянной.

1. Включить в схему эталонный конденсатор С₀ с известной ёмкостью.

2. Переключателем SA замкнуть цепь

3. Переключатель П установить в положение «заряд» и зарядить конденсатор С_0.

4. Переключатель П установить в положение «разряд» и отметить крайнее деление n₀ , до которого передвинется зайчик во время первого колебания в процессе разрядки конденсатора через гальванометр.

5. Пункты 3-4 повторить 5 раз.

Упражнение 2: Определение ёмкости конденсатора.

1. Включить в схему конденсатор с неизвестной ёмкостью С₁.

2. П.п. 2-5 упр. 1 повторить 5 раз (п₁).

3. Включить в схему конденсатор С₂.

4. П.п. 2-5 упр. 1 повторить 5 раз (п₂).

5. Включить в схему конденсатор С_пар, являющийся параллельным соединением С₁ и С₂ (п.п. 2-5 упражнения 1 повторить 5 раз) п_пар.

6. Включить в схему конденсатор С_посл – (последовательное соединение С₁ и С₂) (п.п. 2-5 упражнения 1 повторить 5 раз) п_посл.

Таблица измерений

1. Данные электрической схемы:

– длина от зеркала до шкалы l= 180 мм, Δl = 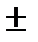0,5 мм;

– ёмкость эталонного конденсатора С₀ = 0,047 мкФ; .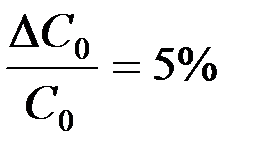

2. Определение отклонения светового «зайчика» n:

№ опыта	n0, дел	Δn0, дел	n1, дел	Δn1, дел	n2, дел	Δn2, дел	(n)пар, дел	Δ(n)пар, дел	(n)посл, дел	Δ(n)посл, дел
Ср. зн.

Обработка результатов измерения.

1. Рассчитать величину динамической постоянной баллистического гальванометра по формуле

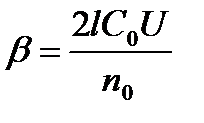
2. Определить относительную погрешность по формуле

,

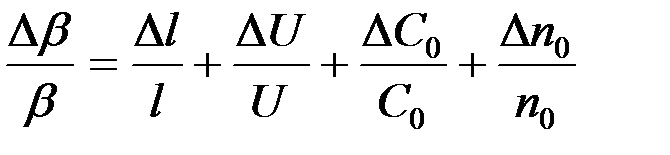ΔU определить из класса точности вольтметра, Δn₀ - сумма приборной и случайной погрешностей.

3. На основе соотношения (10) рассчитать величины С₁, С₂, С_посл, С_пар, подставляя в уравнение вместо

4. Определить соответствующие относительные погрешности по формуле:

.

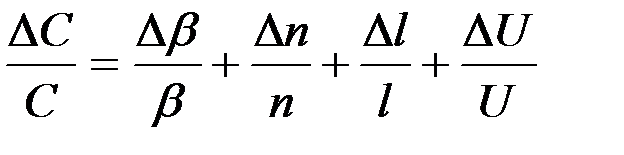5. Найти величины С_пар и С_посл по следующим формулам:

; .

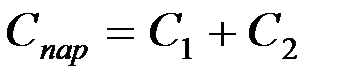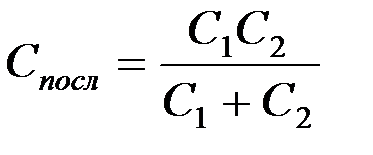6. Сравнить экспериментальные и расчетные значения С_пар и С_посл.

Контрольные вопросы

1.Что такое электроёмкость? В каких единицах она измеряется в системах СИ, СГСЭ?

2. Объясните устройство и принцип действия баллистического гальванометра?

3.Какая электрическая величина измеряется с помощью баллистического гальванометра?

4.Каков физический смысл динамической постоянной β?

5.Какую величину измерит баллистический гальванометр, если к нему подключить источник постоянного тока?

6.Опишите процесс разрядки конденсатора; приведите формулу для тока разряда конденсатора через некоторое сопротивление.

Задача №1

Конденсаторы соединены так, как это показано на рис.1. Электроемкости конденсаторов: 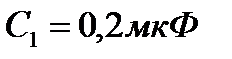, , 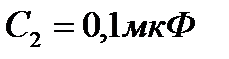, 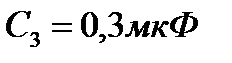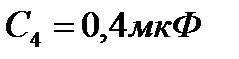. Определить электроемкость С батареи конденсаторов.

Задача №2

Определить электроемкость С схемы , представленной на рис.2, где , , , , .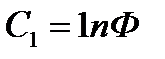

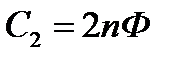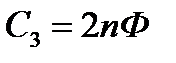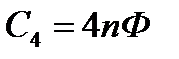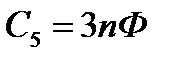С21

С1

С4321

С321

Рис.1

С54321

С1

С21

С321

С4321

С1

С21

С321

С4321

С54321

Рис.2

Рис.3

Задача №3

Пять различных конденсаторов соединены согласно схеме, приведенной на рис.3. Определить электроемкость С₄ , при которой электроемкость всего соединения не зависит от величины электроемкости С₅ . Принять , , .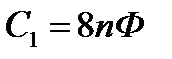

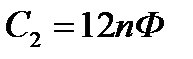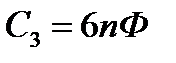Задача №4

Между пластинами плоского конденсатора, заряженного до разности потенциалов 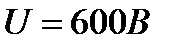, находятся два слоя диэлектриков: стекла толщиной 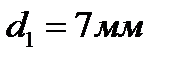и эбонита толщиной 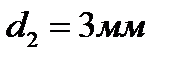. Площадь S каждой пластины конденсатора равна 200см². Найти: 1) электро­емкость С конденсатора; 2) смещение D, напряженность Е поля и падение потенциала U в каждом слое.

Задача №5

В плоский конденсатор вдвинули плитку парафина тол­щиной 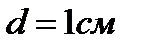, которая вплотную прилегает к его пластинам. Насколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?

Задача №6

Конденсатор емкостью 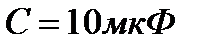периодически заряжается от батареи с ЭДС 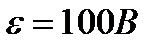и разряжается через катушку в форме кольца диаметром 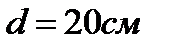, причем плоскость кольца совпадает с плоскостью магнитного меридиана. Катушка имеет 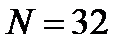витка. Помещенная в центре катушки горизонтальная магнитная стрелка отклоняется на угол 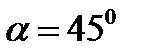. Переключение конденсатора происходит с частотой 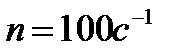. Найти из данных это­го опыта горизонтальную составляющую Н_г напряжен­ности магнитного поля Земли.

Задача №7

Конденсатор емкостью 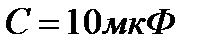периодически заряжается от батареи с ЭДС 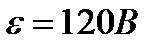и разряжается через соленоид длиной 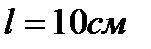. Соленоид имеет 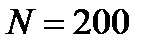витков. Среднее значение напряженности магнитного поля внутри соленоида 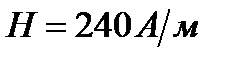. С какой частотой п проис­ходит переключение конденсатора? Диаметр соленоида считать малым по сравнению с его длиной.

Задача №8

На соленоид длиной 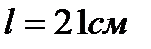и площадью по­перечного сечения 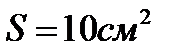надета катушка, состоящая из 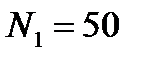витков. Катушка соединена с баллистическим галь­ванометром, сопротивление которого 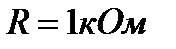. По обмотке соленоида, состоящей из 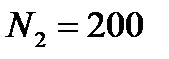витков, идет ток 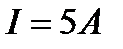. Найти баллистическую постоянную С гальванометра, если известно, что при выключении тока в соленоиде гальванометр дает отброс, равный 30 делениям шкалы (­ Баллистической постоянной гальванометра называется вели­чина, численно равная количеству электричества, которое вызывает отброс по шкале на одно деление). Сопротивлением катушки по сравнению с сопротивлением баллистического гальванометра пренебречь.

Задача №9

Для измерения индукции магнитного поля меж­ду полюсами электромагнита помещена катушка, состоя­щая из 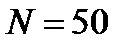витков проволоки и соединенная с баллисти­ческим гальванометром. Ось катушки параллельна направлению магнитного поля. Площадь поперечного сече­ния катушки 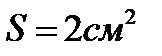. Сопротивление гальванометра 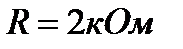; его баллистическая постоянная 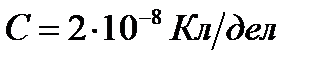. При быстром выдергивании катушки из магнитного поля гальванометр дает отброс, равный 50 делениям шкалы. Найти индукцию В магнитного поля. Сопротивлением ка­тушки по сравнению с сопротивлением баллистического гальванометра пренебречь.

Задача №10

Катушка гальванометра, состоящая из 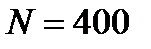витков тонкой проволоки, намотанной на прямоугольный каркас длиной 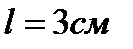и шириной 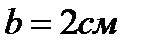, подвешена на нити в магнитном поле с индукцией 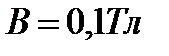. По катушке течет ток 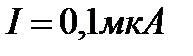. Найти вращающий момент М, действующий на катушку гальванометра, если плоскость катушки: 1) параллельна направлению магнитного поля; 2) составляет угол 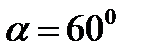с направлением магнитного поля.

Задача №11

На расстоянии 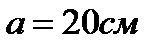от длинного прямолинейного вертикального провода на нити длиной 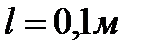и диаметром 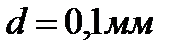висит короткая магнитная стрелка, маг­нитный момент которой 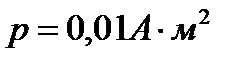. Стрелка находится в плоскости, проходящей через провод и нить. На какой угол 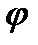повернется стрелка, если по проводу пустить ток 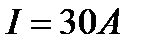? Модуль, сдвига материала нити 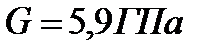. Система экранирована от магнитного поля Земли.

Задача №12

Катушка гальванометра, состоящая из 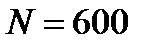витков проволоки, подвешена на нити длиной 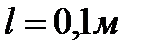и диаметром 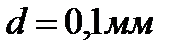в магнитном поле напряженностью 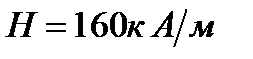так, что ее плоскость параллельна направ­лению магнитного поля. Длина рамки катушки 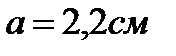и ширина 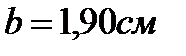. Какой ток I течет по обмотке катушки, если катушка повернулась на угол 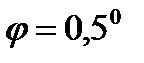? Модуль сдвига материала нити .

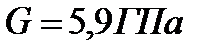Задача №13

Квадратная рамка подвешена на проволоке так, что направление магнитного поля составляет угол 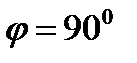с нормалью к плоскости рамки. Сторона рамки 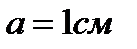. Магнитная индукция поля 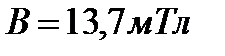. Если по paмке пропустить ток 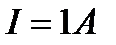, то она поворачивается на, угол 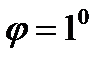. Найти модуль сдвига G материала проволоки. Длина проволоки 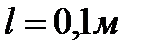, радиус нити ­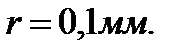

Задача №14

Зеркальце гальванометра подвешено на проволоке длиной 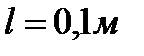и диаметром 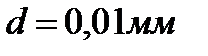. Найти закручивающий момент М, соответствующий отклонению зайчика на величину 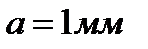по шкале, удаленной на расстояние от зеркальца 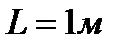. Модуль сдвига материала проволоки .

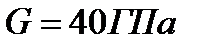Задача №15

При протекании электрического тока через обмотку гальванометра на его рамку с укрепленным на ней зеркальцем действует закручивающий момент 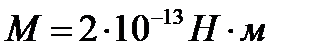, Рамка при этом поворачивается на малый угол 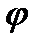. На это закручивание идет работа 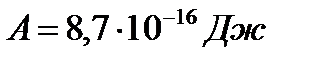. На какое расстояние а переместится зайчик от зеркальца по шкале, удаленной на расстояние 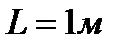от гальванометра?